
题目列表(包括答案和解析)
20.(本题满分12分)小明对本班同学上学的交通方式进行了一次调查,他根据采集的数据,绘制了下面的统计图1和图2.请你根据图中提供的信息,解答下列问题:
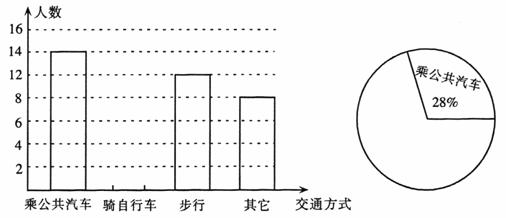
图1 图2
(1)计算本班骑自行车上学的人数,补全图1的统计图;
(2)在图2中,求出“乘公共汽车”部分所对应的圆心角的度数,补全图2的统计图(要求写出各部分所占的百分比);
(3)观察图1和图2,你能得出哪些结论?(只要求写出一条).
19.(本题共2小题,每小题8分,共16分)
(1)计算: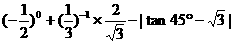 .
.
(2)化简: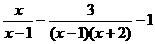 ,并指出x的取值范围.
,并指出x的取值范围.
18.若a、b、c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
① 以a2,b2,c2 的长为边的三条线段能组成一个三角形
② 以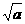 ,
,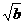 ,
,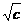 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
③ 以a + b,c + h,h 的长为边的三条线段能组成直角三角形
④ 以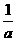 ,
,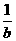 ,
, 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为 .
17.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,那么三辆汽车经过这个十字路口,至少有两辆车向左转的概率为 .
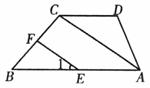
16.如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点O为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1∶2,则线段AC的中点P变换后对应的点的坐标为 .
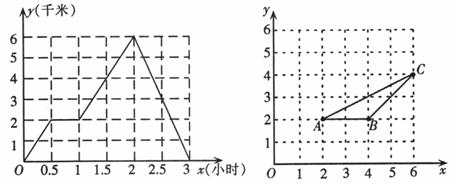
15.如图所示的函数图象反映的过程是:小明从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小明离他家的距离,则小明从学校回家的平均速度为 ____________千米∕小时.
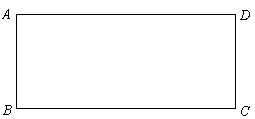
14.如图,梯形ABCD中,AB∥CD,AD = CD,E、F分别是AB、BC的中点,若∠1 = 35°,则∠D = .
13.因式分解:2m2-8n2 = .
12.已知一次函数y = ax + b的图象过点(-2,1),则关于抛物线y = ax2-bx + 3的三条叙述: ① 过定点(2,1), ② 对称轴可以是x = 1,③ 当a<0时,其顶点的纵坐标的最小值为3.其中所有正确叙述的个数是
A.0 B.1 C.2 D.3
11. 当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD,我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC上,折痕EF交AD于F.则∠AFE =
当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD,我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC上,折痕EF交AD于F.则∠AFE =
A.60° B.67.5° C.72° D.75°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com