
题目列表(包括答案和解析)
2.(2008 山东 聊城)已知关于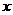 的不等式组
的不等式组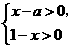 的整数解共有3个,则
的整数解共有3个,则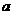 的取值范围是 .
的取值范围是 .
考点七 实践与探索.
例题(2008遵义)某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元。
(1)若该起市同时一次购进甲、两种商品共80件,恰好用去1600元,求能购进甲乙两种商品各多少件?
(2)该超市为使甲、乙两种商品共80元的总利润(利润=售价-进价)不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案。
思路点拨:列不等式(组)解应用题先审题,找出题中的不等关系,设适当的未知数,用含未知数的代数式表示不等关系的两边列出不等式,解不等式.再检验答案的合理性.
 解析:(1)商品进了x件,则乙种商品进了80-x件,依题意得
解析:(1)商品进了x件,则乙种商品进了80-x件,依题意得
10x+(80-x)×30=1600 解得:x=40
即甲种商品进了40件,乙种商品进了80-40=40件。
(2)设购买甲种商品为x件,则购买乙种商品为(80-x)件,依题意可得:
600≤(15-10)x+(40-30)(80-x)≤610 解得: 38≤x≤40
即有三种方案,分别为甲38件,乙42件或甲39件,乙41件或甲40件,乙40件。
[针对训练]
1.(2008四川 乐山)若不等式组
的整数解是关于x的方程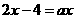 的根,求a的值
的根,求a的值
2.(2008江苏南京)解不等式组. 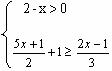 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.

考点六 不等式(组)的特殊解
 例题:(2008成都市) 解不等式组
例题:(2008成都市) 解不等式组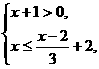 并写出该不等式组的最大整数解.
并写出该不等式组的最大整数解.
思路点拨:求不等式的特殊解的思路是先解不等式(组),求出解集,然后再找出符合
条件的特殊解.
解析: 解不等式x+1>0,得x>-1 ,
解不等式x≤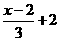 ,得x≤2
,得x≤2
∴不等式得解集为-1<x≤2 ∴该不等式组的最大整数解是2
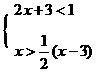 思路点拨:特殊解是解集的一部分,先求出解集,再在里边找出特殊的解,常要借助数轴来求,比较直观准确.
思路点拨:特殊解是解集的一部分,先求出解集,再在里边找出特殊的解,常要借助数轴来求,比较直观准确.
[针对训练]
1、 (2008 河南实验区)解不等式组
(2008 河南实验区)解不等式组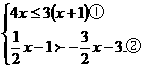 并把解集在已画好的数轴上表示出来。
并把解集在已画好的数轴上表示出来。
2.(2008 河北)把某不等式组中两个不等式的解集表示在数轴上,如图所示,
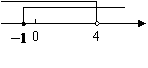 则这个不等式组可能是( )
则这个不等式组可能是( )
A.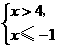 B.
B.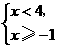 C.
C.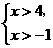 D.
D.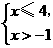
考点五 不等式组的解法
例题.(2008四川省自贡市2008)解不等式组 .
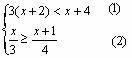
思路点拨:解不等式组是先分别解每个不等式,分别求出它们的解集,然后
 求它们解集的公共部分.
求它们解集的公共部分.
解析:
解不等式(1),得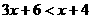 ,
,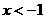
解不等式(2),得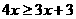 ,
, 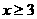
两个不等式的解集无公共部分,∴ 原不等式无解
思路点拨:不等式无公共部分不等式组无解,有公共部分就表示出公共部分.
[针对训练]
1. 泸州市200810.不等式组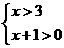 的解集是( )
的解集是( )
A.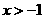 B.
B.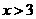 C.
C.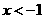 D.
D.
2. (2008 河南)不等式-x-5≤0的解集在数轴上表示正确的是 ( )
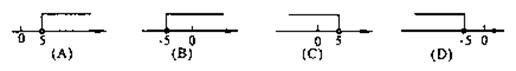
考点四 不等式组及其解集
例题.(2008 四川 凉山州)不等式组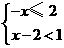 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )

 思路点拨:不等式组的解集是指不等式解集的公共部分,通常是利用数轴,在数轴
思路点拨:不等式组的解集是指不等式解集的公共部分,通常是利用数轴,在数轴
上找解集的公共部分.
解析: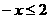 的解集是
的解集是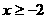 ,
,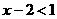 的解集是
的解集是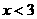 ,所以在数轴表示的公
,所以在数轴表示的公
共部分为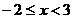 ,选C
,选C
规律总结:不等式组的解集可以利用口诀:大大取大,小小取小,大小中间找或找不到,利用数轴能比较直观的求出.
[针对训练]
1.(2008年江苏省无锡市)不等式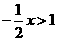 的解集是( )
的解集是( )
A.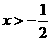 B.
B.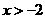 C.
C.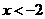 D.
D.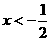
2.(2008 湖南 怀化)不等式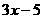 <
<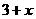 的正整数解有( )
的正整数解有( )
(A)1个 (B)2个 (C)3个 (D)4个
考点三 一元一次不等式的解法.
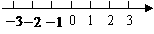 例题:(2008北京)解不等式错误!不能通过编辑域代码创建对象。,并把它的解集在数轴上表示出来.
例题:(2008北京)解不等式错误!不能通过编辑域代码创建对象。,并把它的解集在数轴上表示出来.
 思路点拨:解不等式的利用不等式的基本性质,与接一元一次方程的步骤基本相同,不同的是最后系数化为1时,如果未知数的系数是负数,系数化为1,不等号的方向要改变.
思路点拨:解不等式的利用不等式的基本性质,与接一元一次方程的步骤基本相同,不同的是最后系数化为1时,如果未知数的系数是负数,系数化为1,不等号的方向要改变.
解析:去括号,得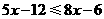 .移项,得
.移项,得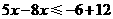 .合并,得
.合并,得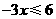 .系数化为1,得
.系数化为1,得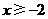 .不等式的解集在数轴上表示如下:
.不等式的解集在数轴上表示如下:
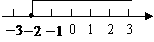 规律总结:解一元一次不等式与解一元一次方程一样,如果有分母不能漏乘不含分母的项,在数轴上表示解集注意实心点与空心点的区别.
规律总结:解一元一次不等式与解一元一次方程一样,如果有分母不能漏乘不含分母的项,在数轴上表示解集注意实心点与空心点的区别.
[针对训练]
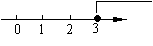
1、(2008湖北武汉)不等式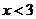 的解集在数轴上表示为( ).
的解集在数轴上表示为( ).
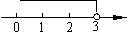
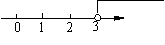 A.
B.
A.
B.
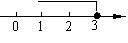 C.
D.
C.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com