24.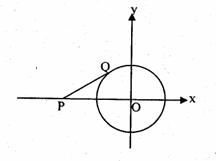 (本题12分)如图，平面直角坐标系中，⊙0的圆心O为坐标原点，半径为1 .长始终为 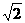的线段PQ的一个端点Q在⊙0上运动，另一个端点P也随之在x轴的负半轴上移动．在运动过程中：

⑴当线段PQ所在的直线与⊙0相切时，求P点的坐标；

⑵当∠OPQ 最大时，求直线PQ的解析式；

⑶当∠OPQ=30°时，求Q点的坐标．

23．(本题10分)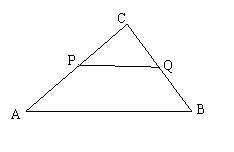如图,△ABC中, ∠C=90⁰,BC=6,AC=8,PQ∥AB,点P在AC上(与点A、C不重合)，点Q在BC上．试问：在AB上是否存在点M，使△PQM为等腰直角三角形？若存在，求PQ的长；若不存在，请说明理由．

22. (本题8分)星光旅行社“五一”前为了了解市区居民“五一”外出旅游情况，采用下列调查方式：

①到机关单位随机选取200名在职人员进行调查；

②到不同的社区随机选取200名居民进行调查；

③到大学城随机选取200名在校学生进行调查．

⑴上述调查方式最合理的是_____________________；

⑵将最合理的调查方式得到的数据制成扇形统计图(如图1),则在这个调查的200个人中“五一”外出旅游的有____________人；

⑶请补全频数分布直方图(如图2)．

(4)请估计市区2 0万居民“五一”外出旅游时间不少于3天的人数．答 　　　人。

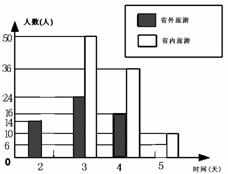
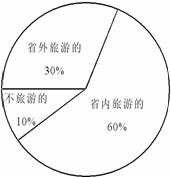
图1　　　　　　　　　　　　　　　 　　　　　　图2

21. 　(本题9分)如图，有长为24m的篱笆，一面利用墙(墙的最大可用长度a为10m)，围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为xm，面积为Sm²．

⑴求S与x的函数关系式；

⑵如果要围成面积为45m²的花圃，AB的长是多少米？

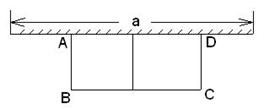⑶能围成面积比45m²更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由．

20．(本题8分)如图，Rt△ABC中，∠C＝90°，按题目所给条件及要求将相应的直角三角形，分割成若干个全等的并且分别与原三角形相似的三角形．画出图形并在图形下方简要说明操作方法．

第(1)图，AC=BC，将ΔABC分割成2个三角形；

第(2)图，AB=2AC，将ΔABC分割成3个三角形；

第(3)图，将ΔABC分割成4个三角形；

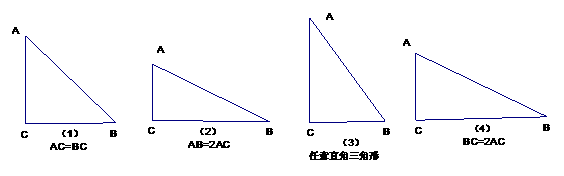第(4)图，BC=2AC，将ΔABC分割成5个三角形；

19. (本题8分)

如图，向口ABCD的外侧画正方形ADGH和正方形DCEF，连结BH、BE和HE，①试猜想△BHE的形状为　　　　　　 三角形.

②向口ABCD的内侧画正方形ADGH和正方形DCEF，连结BH、BE和HE，请画出图形.

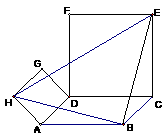判断△BHE的形状，并给出证明.

16．　　 　　　　　　　　17．　　　　　　　　　　 18．　　　　　　　　　　

13．　　　　　　　　　　 14．　　　　　　　　　　 15．　　　　　　　　　　

10．　　　　　　　　　　 11．　　　　　　　　　　 12．　　　　　　　　　　 .

18.已知△ABC为等腰三角形，由A点作BC边的高恰好等于BC边长的一半，则∠BAC的度数为　 ▲　　 .

2007年江苏省高邮中学教改班招生考试

数 学 试 卷

(考试时间：120分钟　 满分150分)