
题目列表(包括答案和解析)
6.已知一元二次方程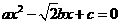 的两个根满足
的两个根满足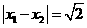 ,且a,b,c分别是
,且a,b,c分别是 的∠A,∠B,∠C的对边.若
的∠A,∠B,∠C的对边.若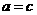 ,求∠B的度数.小敏解得此题的正确答案“
,求∠B的度数.小敏解得此题的正确答案“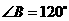 ”后,思考以下问题,请你帮助解答.
”后,思考以下问题,请你帮助解答.
(1)若在原题中,将方程改为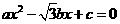 ,要得到
,要得到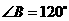 ,而条件“
,而条件“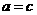 ”不变,那么对应条件中的
”不变,那么对应条件中的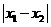 的值作怎样的改变?并说明理由.
的值作怎样的改变?并说明理由.
(2)若在原题中,将方程改为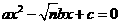 (n为正整数,
(n为正整数,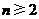 ),要得到
),要得到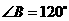 ,而条件“
,而条件“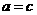 ”不变,那么条件中的
”不变,那么条件中的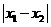 的值应改为多少(不必说明理由)?
的值应改为多少(不必说明理由)?
5.青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2 700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价-进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
(3)在“五·一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
|
打折前一次性购物总金额 |
优惠措施 |
|
不超过300元 |
不优惠 |
|
超过300元且不超过400元 |
售价打九折 |
|
超过400元 |
售价打八折 |
按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
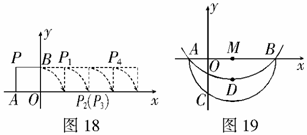
4.如图19,设抛物线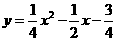 交x轴于
交x轴于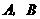 两点,顶点为
两点,顶点为 .以
.以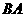 为直径作半圆,圆心为
为直径作半圆,圆心为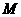 ,半圆交y轴负半轴于
,半圆交y轴负半轴于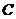 .
.
(1)求抛物线的对称轴;
(2)将 绕圆心
绕圆心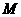 顺时针旋转
顺时针旋转 ,得到
,得到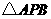 ,如图20.求点
,如图20.求点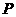 的坐标;
的坐标;
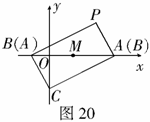
(3)有一动点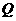 在线段
在线段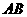 上运动,
上运动, 的周长在不断变化时是否存在最小值?若存在,求点
的周长在不断变化时是否存在最小值?若存在,求点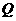 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
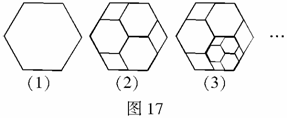
3.如图18,将边长为1的正方形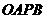 沿x轴正方向连续翻转2 008次,点
沿x轴正方向连续翻转2 008次,点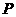 依次落在点
依次落在点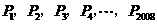 的位置,则
的位置,则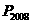 的横坐标
的横坐标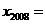 ________.
________.
2.将图17(1)所示的正六边形进行分割得到图17(2),再将图17(2)中最小的某一个正六边形按同样的方式进行分割得到图17(3),再将图17(3)中最小的某一个正六边形按同样的方式进行分割…,则第n个图形中,共有________个正六边形.
1.观察算式:
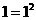 ;
;
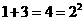 ;
;
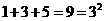 ;
;
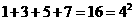 ;
;
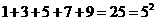 ;……
;……
用代数式表示这个规律(n为正整数):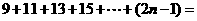 ________.
________.
25. (本小题满分12分)
如图12, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点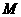 从
从 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向 运动;点
运动;点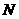 从
从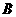 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向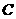 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点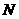 作
作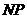 垂直
垂直 轴于点
轴于点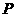 ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.
(1)点 (填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由.
24. (本小题满分10分)
(本小题满分10分)
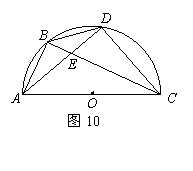
如图10,半圆O为△ABC的外接半圆,AC为直径,D为B C上的一动点.
(1)问添加一个什么条件后,能使得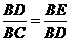 ?请说明理由;
?请说明理由;
(2)若AB∥OD,点D所在的位置应满足什么条件?请说明理由;
(3)如图11,在 (1)和(2)的条件下,四边形AODB是什么特殊的四边形?证明你的结论.

23.(本小题满分8分)
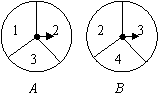
有两个可以自由转动的均匀转盘 都被分成了3等份,并在每一份内均标有数字,如图所示,规则如下:
都被分成了3等份,并在每一份内均标有数字,如图所示,规则如下:
①分别转动转盘 ;②两个转盘停止后观察两个指针所指份内的数字(若指针停在等份线上,那么重转一次,直到指针指向某一份内为止).
;②两个转盘停止后观察两个指针所指份内的数字(若指针停在等份线上,那么重转一次,直到指针指向某一份内为止).
(1)用列表法(或树状图)分别求出“两个指针所指的数字都是方程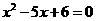 的解”的概率和“两个指针所指的数字都不是方程
的解”的概率和“两个指针所指的数字都不是方程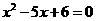 的解”的概率;
的解”的概率;
(2)王磊和张浩想用这两个转盘作游戏,他们规定:若“两个指针所指的数字都是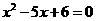 的解”时,王磊得1分;若“两个指针所指的数字都不是
的解”时,王磊得1分;若“两个指针所指的数字都不是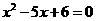 的解”时,张浩得3分,这个游戏公平吗?若认为不公平,请修改得分规定,使游戏对双方公平.
的解”时,张浩得3分,这个游戏公平吗?若认为不公平,请修改得分规定,使游戏对双方公平.

22.(本小题满分8分)
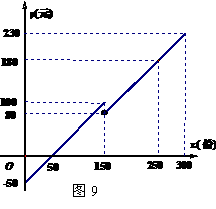 某早餐店每天的利润y(元)与售出的早餐x(份)之间的函数关系如图9所示.当每天售出的早餐超过150份时, 需要增加一名工人.
某早餐店每天的利润y(元)与售出的早餐x(份)之间的函数关系如图9所示.当每天售出的早餐超过150份时, 需要增加一名工人.
(1)该店每天至少要售出 份早餐才不亏本;
(2)求出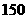 <
<
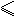
 时,y关于x的函数解析式;
时,y关于x的函数解析式;
(3)要使每天有120元以上的盈利,至少要售出
多少份早餐?
(4)该店每出售一份早餐,盈利多少元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com