
题目列表(包括答案和解析)
5.袋中放有一套(五枚)北京2008年奥运会吉祥物福娃纪念币,依次取出(不放回)两枚纪念币,恰好能够组成“欢迎”的概率是( )
 A.
A.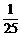 B.
B.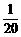
C.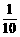 D.
D.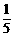
4.二次函数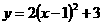 的图像的顶点坐标是 ( )
的图像的顶点坐标是 ( )
A.(1,3) B.(-1,3) C.(1,-3) D.(-1,-3)
3.如图是由相同小正方体组成的立体图形,它的左视图为 ( )
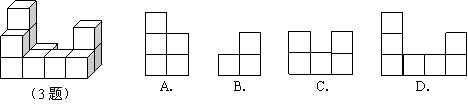
⒈ .4的平方根是 ( )
A.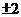 B.2 C. -2 D 16
B.2 C. -2 D 16
2.下列运算正确的是 ( )
A.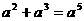 B.
B.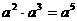 C.
C.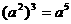 D.
D.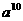 ÷
÷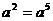
26.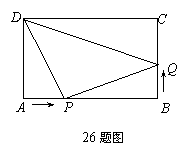 (本小题满分12分)如图,在矩形ABCD中,AB=10cm,BC=6cm,
现有两动点P,Q分别从A,B同时出发,点P在线段AB上沿AB方向作匀速运动,点Q在线段BC上沿BC方向作匀速运动,已知点P的运动速度为1厘米/秒.
(本小题满分12分)如图,在矩形ABCD中,AB=10cm,BC=6cm,
现有两动点P,Q分别从A,B同时出发,点P在线段AB上沿AB方向作匀速运动,点Q在线段BC上沿BC方向作匀速运动,已知点P的运动速度为1厘米/秒.
(1)设点Q的运动速度为 厘米/秒,运动时间为t秒,△DPQ的面积为S,请你求出S与t的函数关系式;
(2)在(1)的条件下,当△DPQ的面积最小时,求BQ的长;
(3)在(1)的条件下,当△DAP和△PBQ相似时,求BQ的长.
(4)设点Q的运动速度为a厘米/秒,问是否存在a的值,使得△ADP与△PBQ和△DCQ这两个三角形都相似?若存在,请求出a的值,并写出此时BQ的长;若不存在,请说明理由.
25.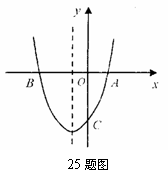 (本小题满分9分)如图,开口向上的抛物线y=ax2+2ax-c与x轴交于点A,B,与y轴交于点C,点A在x轴的正半轴,点B在x的负半轴,OB=OC.
(本小题满分9分)如图,开口向上的抛物线y=ax2+2ax-c与x轴交于点A,B,与y轴交于点C,点A在x轴的正半轴,点B在x的负半轴,OB=OC.
(1)如果点A的坐标为(0,1),求点B的坐标;
(2)求证:ac-2a=1;
(3)在(2)的条件下,问此抛物线的对称轴上是否存在点P,使△PAC的周长最小?若存在,求出点P的坐标,不存在,请说明理由.
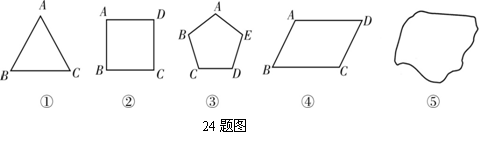
24. (本小题满分10分)某课题学习在探讨一团周长为4a的线圈时,发现了如下两个命题:
命题1:如图①,当线圈做成正三角形ABC时,能被半径为a的圆形纸片完全盖住.
命题2:如图②,当线圈做成正方形ABCD时,能被半径为a的圆形纸片完全盖住.
请你继续探究下列几个问题:
(1)如图③,当线圈做成正五边形ABCDE时,请说明能被半径为a的圆形纸片完全盖住;
(2)如图④,当线圈做成平行四边形ABCD时,能否被半径为a的圆形纸片完全盖住?请说明理由;
(3)如图⑤,当线圈做成任意形状的图形时,是否还能被半径为a的圆形纸片完全盖住?若能盖住,请通过计算说明;若不能盖住,请你说明理由.
23.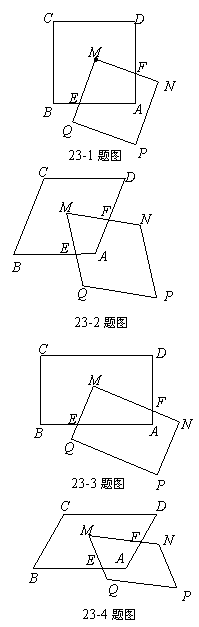 (本小题满分10分)如图1,正方形ABCD和正方形QMNP,∠M =∠B,M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E.
(本小题满分10分)如图1,正方形ABCD和正方形QMNP,∠M =∠B,M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E.
(1)求证:ME = MF.
(2)如图2,若将原题中的“正方形”改为“菱形”,其他条件不变,探索线段ME与线段MF的关系,不必证明.
(3)如图3,若将原题中的“正方形”改为“矩形”,且AB = mBC,其他条件不变,探索线段ME与线段MF的关系,并说明理由.
(4)根据前面的探索和图4,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题;若不能,请说明理由.
22.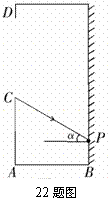 (本小题满分8分)如图,某居民住宅阳台的宽AB为
(本小题满分8分)如图,某居民住宅阳台的宽AB为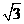 米,在朝向阳光的方向有一玻璃窗CD与地面垂直,该玻璃窗的下端C与地面距离AC=1.5米,上端D与地面距离AD=3.5米,紧靠墙壁的花架上有一盆花(花盆及花的大小忽略不计),记为点P,与地面距离PB=0.5米.如果太阳光线的角度合适,就可以照射到花盆上.
米,在朝向阳光的方向有一玻璃窗CD与地面垂直,该玻璃窗的下端C与地面距离AC=1.5米,上端D与地面距离AD=3.5米,紧靠墙壁的花架上有一盆花(花盆及花的大小忽略不计),记为点P,与地面距离PB=0.5米.如果太阳光线的角度合适,就可以照射到花盆上.
(1)求清晨第一缕照射到花上的太阳光线CP与地面的夹角α的度数;
(2)已知太阳光线与地面的夹角在正午前大约每小时增大15°,在正午后大约每小时减小15°,而这盆花每天需阳光照射3小时才能正常生长.问:如果不移动这盆花的位置,它能否正常生长,请说明理由.
21.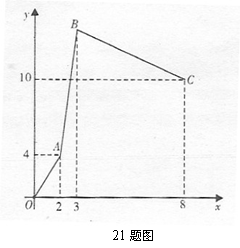 (本小题满分12分)某仓库甲、乙、丙三辆运货车,每辆车只负责进货或出货,每小时的运输量丙车最多,乙车最少,乙车的运输量为每小时6吨,下图是从早晨上班开始库存量y (吨)与时间x (小时)的函数图象,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙工作.
(本小题满分12分)某仓库甲、乙、丙三辆运货车,每辆车只负责进货或出货,每小时的运输量丙车最多,乙车最少,乙车的运输量为每小时6吨,下图是从早晨上班开始库存量y (吨)与时间x (小时)的函数图象,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙工作.
(1)从早晨上班开始,库存每增加2吨,需要几小时?
(2)问甲、乙、丙三辆车,谁是进货车,谁是出货车?
(3)若甲、乙、丙三车一起工作,一天工作8小时,仓库的库存量有什么变化?
(4)请你求出AB段中库存量y (吨)与时间x (小时)的函数解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com