
题目列表(包括答案和解析)
24.(12分)如图a,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题:
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC时(与点B不重合),如图b,线段CF,BD之间的位置关系为
数量关系为
②当点D在线段BC的延长线时,如图c,①中的结论是否仍然成立,为什么三角形ABC满足一个什么条件时间时,
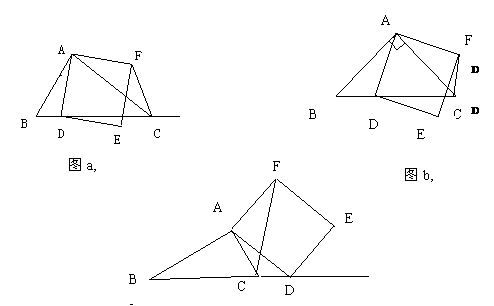

(2)如果AB≠AC, ∠BAC≠90°,点D在线段BC上运动,试探究当CF⊥BC(点C、F重合除外),画出相应图形并说明理由(画图不写作法)。
(3)若AC=4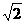 ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值。
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值。
23.(本小题满分10分)
 已知等边三角形纸片
已知等边三角形纸片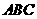 的边长为
的边长为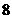 ,
,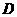 为
为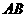 边上的点,过点
边上的点,过点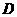 作
作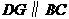 交
交 于点
于点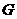 .
.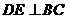 于点
于点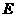 ,过点
,过点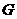 作
作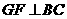 于点
于点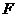 ,把三角形纸片
,把三角形纸片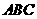 分别沿
分别沿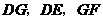 按图1所示方式折叠,点
按图1所示方式折叠,点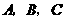 分别落在点
分别落在点 ,
,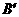 ,
,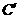 处.若点
处.若点 ,
,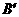 ,
,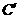 在矩形
在矩形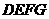 内或其边上,且互不重合,此时我们称
内或其边上,且互不重合,此时我们称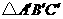 (即图中阴影部分)为“重叠三角形”.
(即图中阴影部分)为“重叠三角形”.
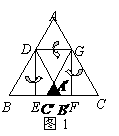
(1)若把三角形纸片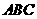 放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点
放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点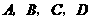 恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形
恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形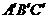 的面积;
的面积;
(2)实验探究:设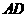 的长为
的长为 ,若重叠三角形
,若重叠三角形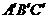 存在.试用含
存在.试用含 的代数式表示重叠三角形
的代数式表示重叠三角形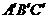 的面积,并写出
的面积,并写出 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
解:(1)重叠三角形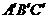 的面积为
;
的面积为
;
(2)用含 的代数式表示重叠三角形
的代数式表示重叠三角形 的面积为
;
的面积为
; 的取值范围为 .
的取值范围为 .
22.(8分)一列快车从甲地驶往乙地,一列慢快车从乙地驶往甲地,两车同时出发,设慢车行驶的个时间为x(h),两车之间的距离为y(km),如图中的折线表示y与x之间的函数关系。根据图像进行以下探究:
(1)甲乙两地之间的距离为 km
(2)解释图中点B的实际意义。
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x 的取值范围; 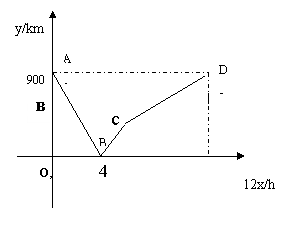

21.(8分)如图所示,山脚下有一棵树AB,小华从点B沿山坡向上走50米到达点D,用高为1.5米的测角仪CD测得树顶的仰角为10°,已知山坡的坡角为15°,求树AB的高(精确到0.1米)
(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18, sin15°≈0.26, cos15°≈0.97,tan15°≈0.27)
|
|
|
|
|
|
|





20.(7分)在学校组织的“喜迎奥运,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90
分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
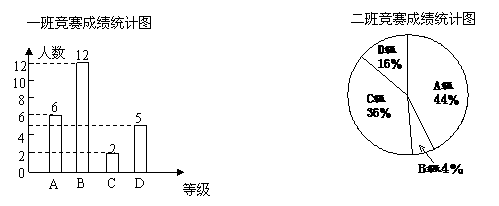
请你根据以上提供的信息解答下列问题:
(1) 此次竞赛中二班成绩在C级以上(包括c级)的人数为---
(2) 请你将表格补充完整:
(3)
|
|
平均分(分) |
中位数(分) |
众数(分) |
|
一班 |
87.6 |
90 |
|
|
二班 |
87.6 |
|
100 |
(4) 请从下列不同角度对这次竞赛成绩的结果进行分析:
① 从平均数和中位数的角度来比较一班和二班的成绩;
② 从平均数和众数的角度来比较一班和二班的成绩;
③ 从B级以上(包括B级)的人数的角度来比较一班和二班的成绩。
19.先化简,在求值(7分)
(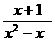 -
-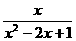 )÷
)÷ 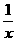 ,其中x=
,其中x=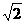 +1
+1
18、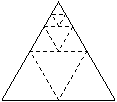 将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:
将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:
|
所剪次数 |
1 |
2 |
3 |
4 |
… |
n |
|
正三角形个数 |
4 |
7 |
10 |
13 |
… |
an |
则an= (用含n的代数式表示).
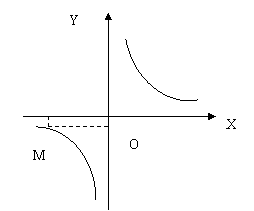
17. 如图所示,反比例函数的解析式为 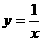 ,点M(2a,
,点M(2a,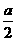 )在第三象限,则a=_
)在第三象限,则a=_

16.现有甲乙两支排球队,每支球队队员的平均身高均为1.85米,方差分别为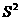 甲 =0.32,
甲 =0.32, 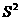 乙=0.26, ,则身高教整齐的球队是_队.
乙=0.26, ,则身高教整齐的球队是_队.
15.抛物线y=2x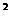 +ax+b的顶点坐标为C(2,-6),则ab=_
+ax+b的顶点坐标为C(2,-6),则ab=_
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com