
题目列表(包括答案和解析)
2. 能画反比例函数的图象,理解反比例函数图象上点的意义,能利用图象理解探索反比例函数的性质.
1. 理解反比例函数的概念,能根据条件确定反比例函数的解析式.
5、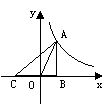
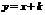 如图6,Rt△ABC(∠ABC=90°)的顶点A是双曲线 与直线
如图6,Rt△ABC(∠ABC=90°)的顶点A是双曲线 与直线
的在第一象限的交点,C为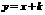 与x轴的交点。若
与x轴的交点。若 1,
1,
(1)求出这两个函数的表达式;(2)求出△ABC的面积。
图-6
3、如图4,A、C是函数 的图象上任意两点,过点A作y轴的垂线,
垂足为B,过点C作y轴的垂线,垂足为D,记RtΔAOB的面积为S1,
Rt△COD的面积为S2,则( ) 图-4
A、S1>S2; B、S1<S2; C、S1 =S2; D、S1和S2的大小关系不能确定
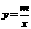
 4、如图5,一次函数
4、如图5,一次函数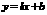 的图象与反比例函数 的图象交于A(-2,1),B(1,n)两点.
的图象与反比例函数 的图象交于A(-2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求 的面积.
图-5
的面积.
图-5
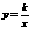
2、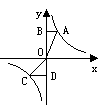 若反比例函数 的图象经过点(a,-a),则a的值为( )。
若反比例函数 的图象经过点(a,-a),则a的值为( )。
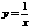 A、2; B、±2; C、-2; D、±4
A、2; B、±2; C、-2; D、±4
1、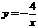 已知反比例函数
的图象在所在像限内,y随x的增大而增大,则k= 。
已知反比例函数
的图象在所在像限内,y随x的增大而增大,则k= 。
3、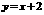 求直线
与双曲线 的交点坐标。 图-3
求直线
与双曲线 的交点坐标。 图-3
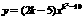 课后思考:
课后思考:
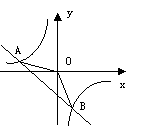
2、如图-3,是一次函数y1=kx+b和反比例函数y2= 的图象,
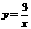 观察图象写出y1>y2时,x的取值范围
。
观察图象写出y1>y2时,x的取值范围
。
1、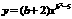
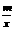 已知函数
的图象是双曲线,则b的值为
。
已知函数
的图象是双曲线,则b的值为
。
7、如图-2示:反函数图象上取任意两点P、Q,并且分别作x轴、y轴
的平行线,与坐标轴围成的矩形的面积S1、S2有什么关系? 。
 能力提升:
能力提升:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com