
题目列表(包括答案和解析)
1.
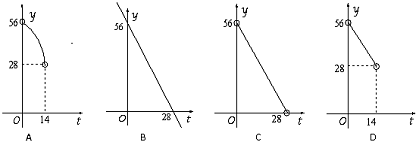 如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形AMND的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是(
)
如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形AMND的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是(
)
4、如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3)。点P、Q同时从原点出发,分别作匀速运动。其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动。当这两点中有一点到达自己的终点时,另一点也停止运动.
(1)设从出发起运动了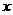 秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或在CB上时的坐标(用含
秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或在CB上时的坐标(用含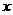 的代数式表示,不要求写出
的代数式表示,不要求写出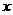 的取值范围);
的取值范围);
(2)设从出发起运动了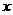 秒,如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半.
秒,如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半.
①试用含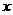 的代数式表示这时点Q所经过的路程和它的速度;
的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应5的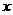 的值和P、Q的坐标;如不可能,请说明理由.
的值和P、Q的坐标;如不可能,请说明理由.
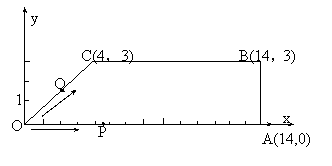 分析:本例是平面直角坐标系与方程、函数、不等式及几何型问题的综合题,解题关键是正确地用
分析:本例是平面直角坐标系与方程、函数、不等式及几何型问题的综合题,解题关键是正确地用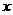 的代数式表示出点的坐标,特别注意直线PQ同时把梯形OABC的面积也分成相等的两部分要分两类讨论.
的代数式表示出点的坐标,特别注意直线PQ同时把梯形OABC的面积也分成相等的两部分要分两类讨论.
作业:
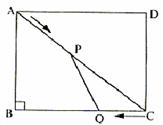
3、如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2。(1)求面积S与时间t的关系式;
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。
分析:本题是一个动态几何问题,也是一个数形结合的典型问题,综合性较强。
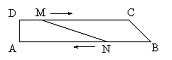
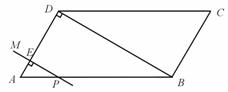
2、如图,在平行四边形ABCD中,AD=4 cm,∠A=60°,BD⊥AD. 一动点P从A出发,以每秒1 cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD .
(1) 当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2) 当点P运动2秒时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒1 cm的速度匀速运动,在BC上以每秒2 cm的速度匀速运动. 过Q作直线QN,使QN∥PM. 设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为S cm2 .
 ① 求S关于t的函数关系式;
① 求S关于t的函数关系式;
② (附加题) 求S的最大值.
1、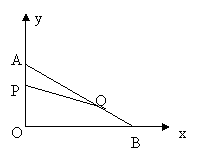 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ与△AOB相似? (3) 当t为何值时,△APQ的面积为
如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ与△AOB相似? (3) 当t为何值时,△APQ的面积为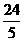 个平方单位?
个平方单位?
3、
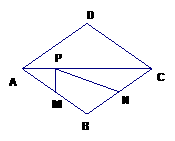
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是线段AC上的两个动点,分别从A、C两点以相同的速度1㎝/s向C、A运动,若BD=12㎝,AC=16㎝,当t
时,四边形DEBF为平行四边形;当时间t=
时,四边形DEBF为矩形。
如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是线段AC上的两个动点,分别从A、C两点以相同的速度1㎝/s向C、A运动,若BD=12㎝,AC=16㎝,当t
时,四边形DEBF为平行四边形;当时间t=
时,四边形DEBF为矩形。
例题讲解:
2、若点P为边长为5的等边三角形内的一个动点,作PD⊥BC于点D,PE⊥AC于点E,PF⊥AB于点F,则PD+PE+PF= ;反之,若PD=6,PE=10,PF=8,则等边△ABC的面积为 ;
1、如图,点P是边为1的菱形ABCD对角线AC的一个动点,点M、N分别是AB、BC的中点,则MP+NP的最小值是 ;
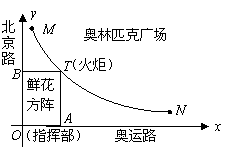
2.(2008江苏镇江)如图,奥运圣火抵达某市奥林匹克广场后,沿图中直角坐标系中的一段反比例函数图象传递.动点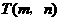 表示火炬位置,火炬从离北京路10米处的
表示火炬位置,火炬从离北京路10米处的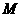 点开始传递,到离北京路1000米的
点开始传递,到离北京路1000米的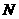 点时传递活动结束.迎圣火临时指挥部设在坐标原点
点时传递活动结束.迎圣火临时指挥部设在坐标原点 (北京路与奥运路的十字路口),
(北京路与奥运路的十字路口),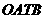 为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000平方米(路线宽度均不计).
为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000平方米(路线宽度均不计).
(1)求图中反比例函数的关系式(不需写出自变量的取值范围);
(2)当鲜花方阵的周长为500米时,确定此时火炬的位置(用坐标表示);
 (3)设
(3)设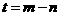 ,用含
,用含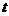 的代数式表示火炬到指挥部的距离;当火炬离指挥部最近时,确定此时火炬的位置(用坐标表示).
的代数式表示火炬到指挥部的距离;当火炬离指挥部最近时,确定此时火炬的位置(用坐标表示).
1.(2008福建宁德)蓄电池电压为定值,使用此电源时,电流I(安)与电阻R(欧)之间关系图象如图所示,若点P在图象上,则I与R(R>0)的函数关系式是______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com