
题目列表(包括答案和解析)
3.如图,在不等边 中,
中,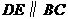 ,
,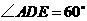 ,图中等于
,图中等于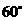 的角还有______________.
的角还有______________.
2.如图,已知直线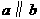 ,
,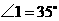 ,则
,则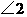 的度数是 .
的度数是 .
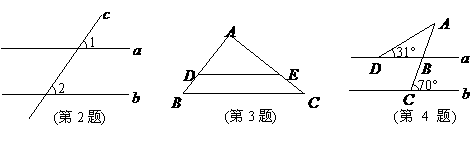
1. 如图,延长线段 到
到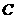 ,使
,使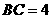 ,
,
若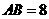 ,则线段
,则线段 是
是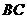 的 倍.
的 倍.
26、(08天津)已知Rt△ABC中,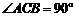 ,
,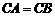 ,有一个圆心角为
,有一个圆心角为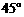 ,半径的长等于
,半径的长等于 的扇形
的扇形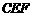 绕点C旋转,且直线CE,CF分别与直线
绕点C旋转,且直线CE,CF分别与直线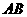 交于点M,N.
交于点M,N.
(1)当扇形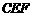 绕点C在
绕点C在 的内部旋转时,如图①,求证:
的内部旋转时,如图①,求证: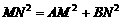 ;
;
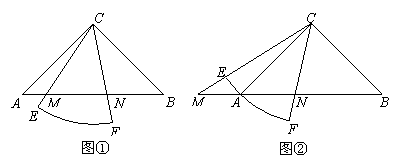 (2)当扇形CEF绕点C旋转至图②的位置时,关系式
(2)当扇形CEF绕点C旋转至图②的位置时,关系式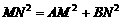 是否仍然成立?若成立,请证明;若不成立,请说明理由.
是否仍然成立?若成立,请证明;若不成立,请说明理由.
(08恩施)如图11,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,
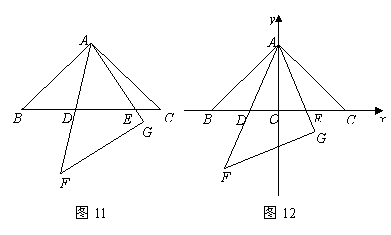 A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A
A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A
旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,
CD=n.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图12).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD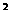 +CE
+CE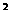 =DE
=DE .
.
(4)在旋转过程中,(3)中的等量关系BD +CE
+CE =DE
=DE 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.
(08大庆)如图①,四边形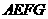 和
和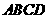 都是正方形,它们的边长分别为
都是正方形,它们的边长分别为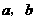 (
(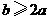 ),且点
),且点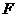 在
在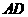 上(以下问题的结果均可用
上(以下问题的结果均可用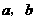 的代数式表示).
的代数式表示).
(1)求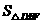 ;
;
(2)把正方形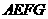 绕点
绕点 按逆时针方向旋转45°得图②,求图②中的
按逆时针方向旋转45°得图②,求图②中的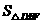 ;
;
(3)把正方形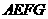 绕点
绕点 旋转一周,在旋转的过程中,
旋转一周,在旋转的过程中,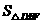 是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由.
是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由.
(08淄博)正方形ABCD的对角线交点为O,两条对角线把它分成了四个面积相等的三角形。
(1)平行四边形ABCD的两条对角线交点为O,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试判断S1,S2,S3,S4的关系,并加以证明;
(2)四边形ABCD的两条对角线互相垂直,交点为O,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试判断S1,S2,S3,S4的关系,并加以证明;
(3)四边形ABCD的两条对角线交点为O,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试判断S1,S2,S3,S4的关系,并加以证明;
(4)四边形ABCD的两条对角线相等,交点为O,∠BAC=∠BDC,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试只用S1,S3或只用S2,S4表示四边形ABCD的面积S.
(1)如图1,已知:直线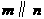 ,
,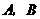 为直线
为直线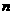 上两点,
上两点,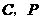 为直线
为直线 上两点,请写出图中,
上两点,请写出图中, 和
和 面积之间的数量关系: ;
面积之间的数量关系: ;
(2)如图2,边长为6的正三角形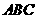 ,
,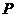 是
是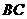 边上一点,且
边上一点,且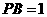 ,以
,以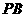 为一边作正三角形
为一边作正三角形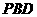 ,则
,则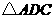 的面积为 ;
的面积为 ;
(3)如图3,边长为6的正三角形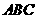 ,
,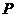 是
是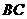 边上一点,且
边上一点,且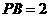 ,以
,以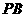 为一边作正三角形
为一边作正三角形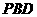 ,则
,则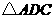 的面积为 ;
的面积为 ;
(4)根据上述计算的结果,你发现了怎样的规律?提出自己的猜想并依据图4予以证明.
(5)如图5,有一块正三角形草皮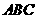 ,由于某种原因,需要将三角形草皮
,由于某种原因,需要将三角形草皮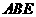 移植到三角形的草皮
移植到三角形的草皮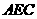 的右侧,成为一块新的三角形草皮
的右侧,成为一块新的三角形草皮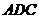 (
( 三点要在一条直线上),并保持其面积不变,请你画图说明如何确定点
三点要在一条直线上),并保持其面积不变,请你画图说明如何确定点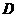 的位置.
的位置.
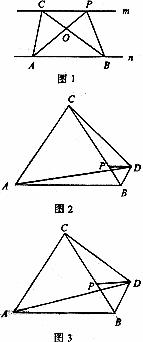
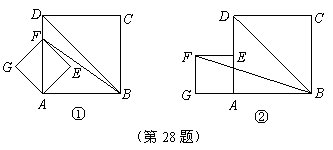
(1)如图12-1,已知直线m∥n,A,B为直线n上的两点,C,D为直线m上的两点.
①请你判断△ABC与△ABD的面积具有怎样的关系?
②若点D在直线m上可以任意移动,△ABD的面积是否发生变化?并说明你的理由.
(2)如图12-2,已知:在四边形ABCD中,连结AC,过点D作EF∥AC,P为EF上任意一点(与点D不重合).请你说明四边形ABCD的面积与四边形ABCP的面积相等.
 (3)如图12-3是一块五边形花坛的示意图.为了使其更规整一些,园林管理人员准备将其修整为四边形,根据花坛周边的情况,计划在BC的延长线上取一点F,沿EF取直,构成新的四边形ABFE,并使得四边形ABFE的面积与五边形ABCDE的面积相等.请你在图15-3中画出符合要求的四边形ABFE,并说明理由.
(3)如图12-3是一块五边形花坛的示意图.为了使其更规整一些,园林管理人员准备将其修整为四边形,根据花坛周边的情况,计划在BC的延长线上取一点F,沿EF取直,构成新的四边形ABFE,并使得四边形ABFE的面积与五边形ABCDE的面积相等.请你在图15-3中画出符合要求的四边形ABFE,并说明理由.
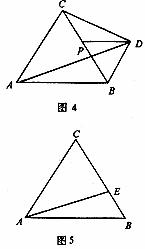
(09七中模拟)已知正方形ABCD的边长为4,G是边CD上一点,以CG为边作正方形GCEF.
(1)如图1,当点G与点D重合时,△BDF的面积为 。
(2)如图2,当点G是CD的中点时,△BDF的面积为 。
(3)如图3,当点G是CD边上的任意位置时,△BDF的面积为 。
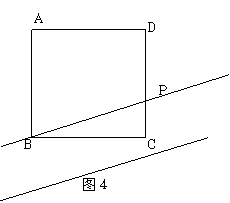
解决问题:张三家有一块正方形的土地(如图4)由于修建高速公路被占去了一块三角形的地方BCP.现决定在DP的右侧补给张三一块土地,补偿后的土地为四边形ABMD,要求补偿后的四边形ABMD的面积与原来的正方形ABCD的面积相等,且M在BP的延长线上,请你在图中画出点M的位置,并简要说明理由。
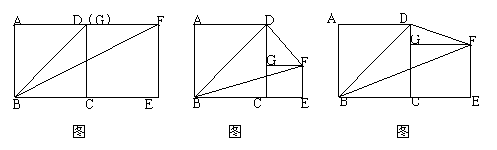
在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图1,2,3是旋转三角板得到的图形中的3种情况研究:
(1)三角板绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图2加以证明.
(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长;若不能,请说明理由.
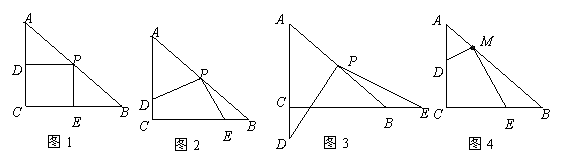 (3)若将三角板的直角顶点放在斜边AB上的M处,且AM∶MB=1∶3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合如图4加以证明.
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM∶MB=1∶3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合如图4加以证明.
(08福州)如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
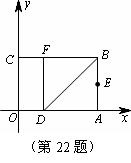 (1)直接写出点E、F的坐标;
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
(08潍坊)如图,矩形纸片 中,
中, ,将纸片折叠,使顶点
,将纸片折叠,使顶点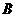 落在边
落在边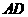 的
的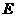 点上,折痕的一端
点上,折痕的一端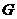 点在边
点在边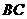 上,
上,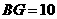 .
.
(1)当折痕的另一端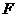 在
在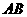 边上时,如图(1),求
边上时,如图(1),求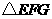 的面积;
的面积;
 (2)当折痕的另一端
(2)当折痕的另一端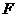 在
在 边上时,如图(2),证明四边形
边上时,如图(2),证明四边形 为菱形,并求出折痕
为菱形,并求出折痕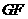 的长.
的长.
(07绍兴)课外兴趣小组活动时,许老师出示了如下问题:
如图1,己知四边形ABCD中,AC平分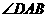 ,
, 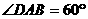 ,
, 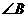 与
与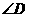 互补,求证:
互补,求证: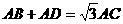 .
.
小敏反复探索,不得其解.她想,若将四边形ABCD特殊化,看如何解决该问题.
(1)特殊情况入手添加条件:“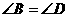 ”, 如图2,可证
”, 如图2,可证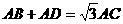 .(请你完成此证明)
.(请你完成此证明)
(2)解决原来问题受到(1)的启发,在原问题中,添加辅助线:如图3,过C点分别作AB、AD的垂线,垂足分别为E、F.(请你补全证明)
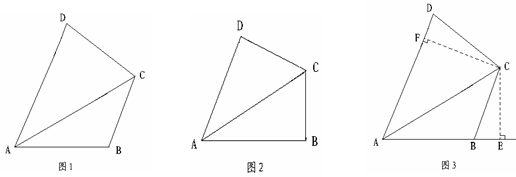
(1)如图13①在正方形ABCD中,对角线AC、BD交于点O,在BD上有一动点P,PE⊥AB,PF⊥AD,垂足分别为E、F,通过观察或测量,猜想OE、OF满足的数量关系,并证明你的猜想.
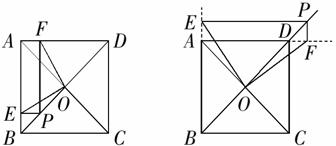 (2)若点P移动到BD的延长线上(如图13②),其他条件不变,那么你在(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
(2)若点P移动到BD的延长线上(如图13②),其他条件不变,那么你在(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
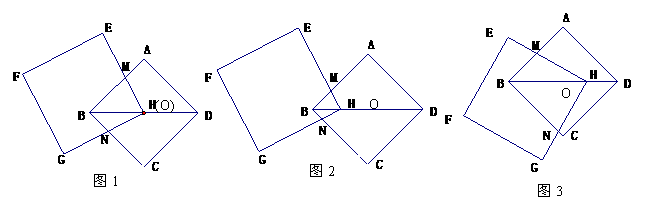
在△ABC中,AB=AC,AC⊥BA,M为BC边中点,一等腰直角三角尺的直角顶点P在BC边上移动,两直角边分别与AB,AC交于E,F两点且斜边与BC平行.
(1)在图13-1中,当三角尺的直角顶点P恰好移动到M点时,请你通过观察、测量,猜想并写出ME与M F满足的数量关系及位置关系,然后证明你的猜想;
(2)当三角尺的直角顶点P沿BC方向移动到图13-2所示的位置时,请你通过观察、测量、猜想并写出ME与MF满足的数量关系及位置关系,然后证明你的猜想;
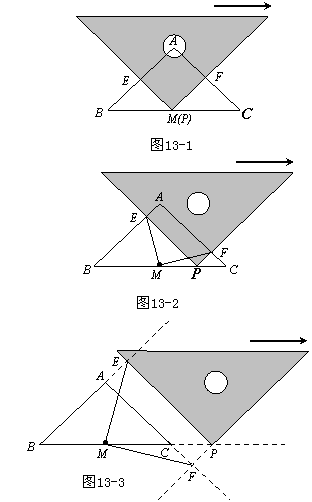 (3)当三角尺在(2)的基础上沿BC方向继续向右平移到图13-3所示的位置(点P在线段BC的延长线上,三角尺两直角边所在直线与△ABC的两边BA,AC的延长线分别交于点E,F,且点P与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)
(3)当三角尺在(2)的基础上沿BC方向继续向右平移到图13-3所示的位置(点P在线段BC的延长线上,三角尺两直角边所在直线与△ABC的两边BA,AC的延长线分别交于点E,F,且点P与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)
(08宁夏)如图,在边长为4的正方形 中,点
中,点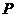 在
在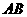 上从
上从 向
向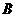 运动,连接
运动,连接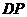 交
交 于点
于点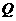 .
.
(1)试证明:无论点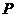 运动到
运动到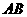 上何处时,都有△
上何处时,都有△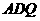 ≌△
≌△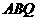 ;
;
 (2)当点
(2)当点 在
在 上运动到什么位置时,△
上运动到什么位置时,△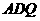 的面积是正方形
的面积是正方形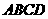 面积的
面积的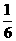 ;
;
(3)若点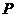 从点
从点 运动到点
运动到点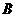 ,再继续在
,再继续在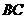 上运动到点
上运动到点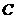 ,在整个运动过程中,当点
,在整个运动过程中,当点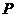 运动到什么位置时,△
运动到什么位置时,△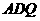 恰为等腰三角形.
恰为等腰三角形.
(08兰州)如图15,平行四边形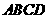 中,
中,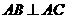 ,
,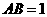 ,
,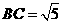 .对角线
.对角线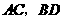 相交于点
相交于点 ,将直线
,将直线 绕点
绕点 顺时针旋转,分别交
顺时针旋转,分别交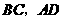 于点
于点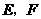 .
.
(1)证明:当旋转角为 时,四边形
时,四边形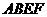 是平行四边形;
是平行四边形;
(2)试说明在旋转过程中,线段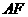 与
与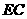 总保持相等;
总保持相等;
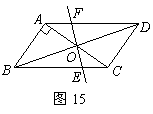 (3)在旋转过程中,四边形
(3)在旋转过程中,四边形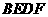 可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时
可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时 绕点
绕点 顺时针旋转的度数.
顺时针旋转的度数.
如图1,正方形ABCD是边长为1的正方形,正方形EFGH的边HE、HG与正方形ABCD
的边AB、BC交于点M、N,顶点H在对角线BD上移动,设点M、N到BD的距离分别
是hm、hn,四边形MBNH的面积是S;
(1)当顶点H和正方形ABCD的中心O重合时(图1),S= , hm+ hn= .
(2)若顶点H为OB的中点(图2),则S= , hm+ hn = .
(以上两题只要求写出结果,不用证明)
(3)按要求利用图3完成下列问题:
我们准备探索:当BH=n时,S= ,hm+ hn = ;
① 在上面的横线上填上你的结论;
②
 证明你得到的结论.
证明你得到的结论.
(08山东临沂)已知∠MAN,AC平分∠MAN。
⑴在图1中,若∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;
⑵在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则⑴中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
⑶在图3中:
①若∠MAN=60°,∠ABC+∠ADC=180°,则AB+AD=____AC;
 ②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC(用含α的三角函数表示),并给出证明。
②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC(用含α的三角函数表示),并给出证明。
(七中模拟)已知,∠POQ=60,点A在射线OP上,点B在射线OQ上。△ABC是等边三角形,点M是△ABC的外接圆的圆心。
(1) 当OA=OB时,如图1,说明点M在∠POQ的角平分线上。
(2) 当OA<OB时,作ME⊥OP于点E,MF⊥OQ于点F,如图2.
① 求证:∠CBQ=∠OAB;
② 求证:△AEM≌△BFM;
③ 求证:点M在∠POQ的平分线上。
(3)判断:当OA>OB时,点M是否在∠POQ的角平分线上;答: (填是 或 否 )
(4)综上所述,可得的结论

(七中模拟)已知,将两块等腰直角三角板ABC和ADE如图放置,再以CE,CB为边作平行四边形CEHB,连DC,CH。
a) 如图1,连接DH,请你判断△DHC的形状,猜想CH与CD之间有何数量关系?请说明理由。
b) 将图1中的△ADE绕A点逆时针旋转45°得图2,请你猜想CH与CD之间的数量关系 。
c) 将图1中的△ADE绕A点顺时针旋转a(0°<a<45°)得图3,(2)中的猜想是否还成立,若成立,请给出证明;不成立,说明理由。
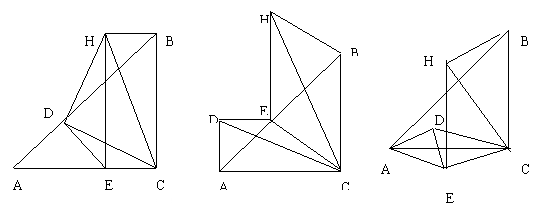
(七中模拟)如图13-1,以△ABC的边AB,AC为直角边作等腰△ABE和△ACD,M是BC的中点.
(1)若∠BAC=90°,如图13-1.请你猜想线段DE,AM的数量关系,并证明你的结论;
(2)若∠BAC≠90°.
①如图13-2.请你猜想线段DE,AM的数量关系,并证明你的结论;
 ②如图13-3.请你判断线段DE,AM的数量关系.
②如图13-3.请你判断线段DE,AM的数量关系.
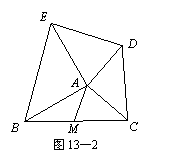
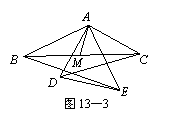
(七中模拟)如图1,△ABC中,AD为BC边上的的中线,则S△ABD= S△ADC.
实践探究
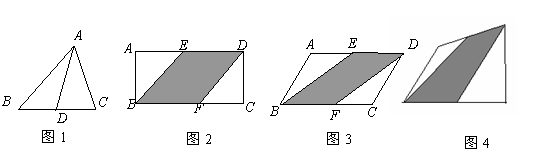 (1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴和S矩形ABCD之间满足的关系式为
;
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴和S矩形ABCD之间满足的关系式为
;
(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴和
S平行四边形ABCD之间满足的关系式为 ;
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴和
S四边形ABCD之间满足的关系式为 ;
解决问题:
 (4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和是多少?即求S1+ S2+ S3+ S4=?
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和是多少?即求S1+ S2+ S3+ S4=?
(七中模拟)(1)如果△ABC的面积是S,E是BC的中点,连结AE(图1),则△AEC的面积是 .
 (2)在△ABC的外部作△ACD,F是AD的中点,连结CF(图2),若四边形ABCD的面积是S,则四边形AECF的面积是 ;
(2)在△ABC的外部作△ACD,F是AD的中点,连结CF(图2),若四边形ABCD的面积是S,则四边形AECF的面积是 ;
(3)若任意四边形ABCD的面积是S,E、F分别是一组对边AB,CD的中点,连结AF,
CE(图3),则四边形AECF的面积是 ;
拓展与应用
(1)若八边形ABCDEFGH的面积是100,K,M,N,O,P,Q分别是AB,BC,CD,EF,FG,GH的中点,连结KH,MG,NF,OD,PC,QB(图4),则图中阴影部分的面积是 ;
(2)四边形ABCD的面积是100,E,F分别是一组对边AB,CD上的点,且AE=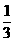 AB,CF=
AB,CF=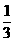 CD,连结AF,CE(图5)则四边形AECF的面积是 ;
CD,连结AF,CE(图5)则四边形AECF的面积是 ;
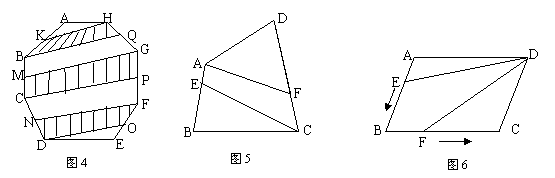
(3)平行四边形ABCD的面积为2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动.点F从点B出发沿BC以每秒 个单位的速度向点C运动.E、F分别从点A,B同时出发,当其中一点到达端点时,另一点也随之停止运动。请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
个单位的速度向点C运动.E、F分别从点A,B同时出发,当其中一点到达端点时,另一点也随之停止运动。请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
(桥西模拟)(1)如图1,P为⊙O内任意一点,连结OP,再过P作AB⊥OP交⊙O 于A、B两点,则可以得到弦AB被点P平分,理由是 。
(2)探索:如图2,P为∠MON平分线上一点,请你作一条“弦”AB(即点A在OM上,点B在ON上),使AB被点P平分。
 (3)联想:结合小黑板老师给出的规律(如图3)探究如图4,P为∠MON内任一点,是否存在过点P的弦AB,使AB被点P平分?若存在,给出画图方案;若不存在,简要说明理由。
(3)联想:结合小黑板老师给出的规律(如图3)探究如图4,P为∠MON内任一点,是否存在过点P的弦AB,使AB被点P平分?若存在,给出画图方案;若不存在,简要说明理由。
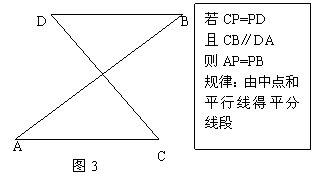

24、(芜湖08)如图,在梯形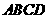 中,
中,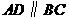 ,
,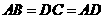 ,
,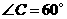 ,
,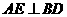 于点E,F是CD的中点,DG是梯形
于点E,F是CD的中点,DG是梯形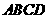 的高.
的高.
(1)求证:四边形AEFD是平行四边形;
(2)设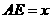 ,四边形DEGF的面积为y,求y关于x的函数关系式.
,四边形DEGF的面积为y,求y关于x的函数关系式.
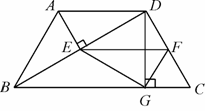
25(08大连).如图25-1,正方形ABCD和正方形QMNP,∠M =∠B,M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E.
⑴求证:ME = MF.
⑵如图25-2,若将原题中的“正方形”改为“菱形”,其他条件不变,探索线段ME与线段MF的关系,并加以证明.
⑶如图25-3,若将原题中的“正方形”改为“矩形”,且AB = mBC,其他条件不变,探索线段ME与线段MF的关系,并说明理由.
⑷根据前面的探索和图25-4,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题;若不能,请说明理由.

23、(08烟台市)如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)设△BEF的面积为S,求S的取值范围.
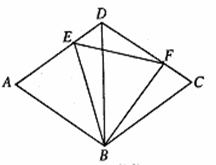
22、(08武汉)正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F。如图1,当点P与点O重合时,显然有DF=CF.
⑴如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E。
①求证:DF=EF;
②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;
⑵若点P在线段OC上(不与点O、C重合),PE⊥PB且PE交直线CD于点E。请完成图3并判断⑴中的结论①、②是否分别成立?若不成立,写出相应的结论(所写结论均不必证明)
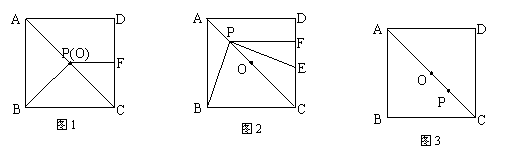
21、(成都08)已知:在梯形ABCD中,AD∥BC,AB = DC,E、F分别是AB和BC边上的点.
(1)如图①,以EF为对称轴翻折梯形ABCD,使点B与点D重合,且DF⊥BC.若AD =4,BC=8,求梯形ABCD的面积 的值;
的值;
(2)如图②,连接EF并延长与DC的延长线交于点G,如果FG=k·EF(k为正数),试猜想BE与CG有何数量关系?写出你的结论并证明之.
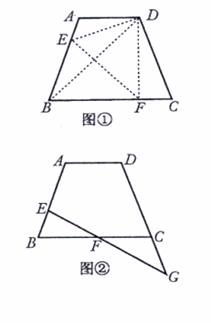
20、(恩施08)如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC已知AB=5,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小?
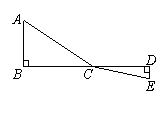 (3)根据(2)中的规律和结论,请构图求出代数式
(3)根据(2)中的规律和结论,请构图求出代数式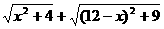 的最小值.
的最小值.
19、(盐城08)如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90º.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .
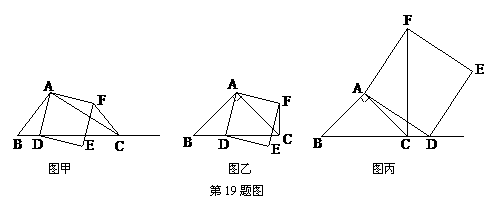 ②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90º,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
(3)若AC= ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com