
题目列表(包括答案和解析)
34.解:(1)设购买甲种树苗x株,则购买乙种树苗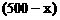 株。
株。
由题意得: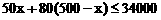 解这个不等式,得:
解这个不等式,得: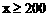
(2)设见(1),由题意得 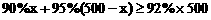
解这个不等式,得: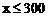
又设购买两种树苗的费用之和为y元,则 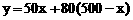
即: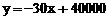
由一次函数的增减性知:当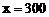 时,所用的购树费用最少,费用是31000元。
时,所用的购树费用最少,费用是31000元。
33.[提示]由题意,相遇前甲走了2小时,及“当甲回到A地时,乙离A地还有2千米”,可得列方程组的另一个相等关系:甲、乙同向行2小时,相差2千米.设甲、乙两人的速度分别为x 千米/时,y 千米/时,则
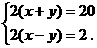
[答案]甲的速度为5.5千米/时,乙的速度为4.5千米/时
32.解:(1)抽样的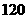 户家庭一年共可节约用水:
户家庭一年共可节约用水:
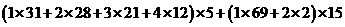
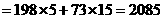 .
.
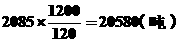 。
。
答:该社区一年共可节约用水 吨.
吨.
(2)设既要改造水龙头又要改造马桶的家庭共有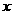 户,则只改造水龙头不改造马桶的家庭共有
户,则只改造水龙头不改造马桶的家庭共有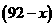 户,只改造马桶不改造水龙头的家庭共有
户,只改造马桶不改造水龙头的家庭共有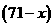 户.
户.
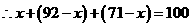 ,
,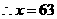 (
( 户).
户).
答:既要改造水龙头又要改造马桶的家庭共有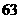 户.
户.
31.(1)证明: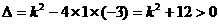
 原方程有两个不相等的实数根.
原方程有两个不相等的实数根.
第2小题,略(答案不唯一)
30.解:(1)设文化衫和相册的价格分别为x元和y 元,则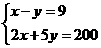
解得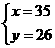 .
.
答:一件文化衫和一本相册的价格分别为35元和26元.
(2)设购买文化衫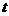 件,则购买相册
件,则购买相册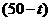 本,
本,
则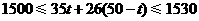 ,
,
解得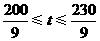 .
.
∵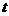 为正整数,∴
为正整数,∴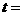 23,24,25,即有三种方案.
23,24,25,即有三种方案.
第一种方案:购文化衫23件,相册27本,此时余下资金293元;
第二种方案:购文化衫24件,相册26本,此时余下资金284元;
第三种方案:购文化衫25件,相册25本,此时余下资金275元;
所以第一种方案用于购买教师纪念品的资金更充足.
29.分析:第(1)问利用二元一次方程组求钢笔和练习本的单价,第(2)问通过一元一次不等式求出最多可买多少个练习本.
解:(1)设买一支钢笔需x元,买一个练习本需y元,依题意: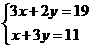
解之得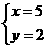 .
.
(2)设买的练习本为z个,
则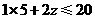 ,得
,得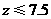 .
.
因为z为非负整数,所以z的最大值为7.
答:(1)买1支钢笔需5元,1个练习本需2元.(2)小明最多可买7个练习本.
28.解:解不等式①得: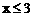 解不等式②得:
解不等式②得: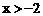

27。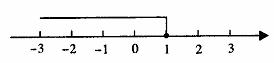 解:解不等式(1)得:
解:解不等式(1)得: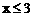 解不等式(2)得:
解不等式(2)得: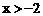
∴原不等式的解集为: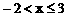 在数轴上表示如下:
在数轴上表示如下:

26.解: 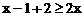
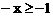
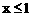
25.解:方程两边同乘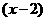 ,得
,得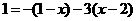 .
.
解这个方程,得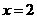 .
.
检验:当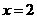 时,
时,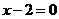 ,所以
,所以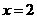 是增根,原方程无解
是增根,原方程无解
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com