
题目列表(包括答案和解析)
6.点A、B、C是平面内不在同一条直线上的三点,点D是平面内任意一点,若A、B、C、D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有 ( )
A.1个 B.2个 C.3个 D.4个
5.为了解居民节约用水的情况,增强居民的节水意识,下表是某个单元的住户当月用水量的调查结果:
|
住户(户) |
2 |
4 |
5 |
1 |
|
月用水量(方/户) |
2 |
4 |
6 |
10 |
则关于这12户居民月用水量,下列说法错误的是 ( )
A.中位数 6方 B.众数6方 C.极差8方 D.平均数5方
4.用一个平面去截一个几何体,不能截得三角形截面的几何体是 ( )
A.圆柱 B.圆锥 C.三棱柱 D.正方形
3. 把61万用科学记数法可表示为 ( )
A.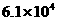 B.
B.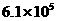 C.
C.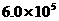 D.
D. 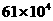
2.把多项式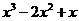 分解因式结果正确的是
( )
分解因式结果正确的是
( )
A.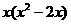 B.
B.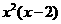 C.
C.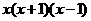 D.
D.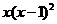
1.下列运算正确的是 ( )
A.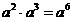 B.
B.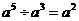 C.
C.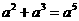 D.
D.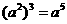
23.(本题满分11分)
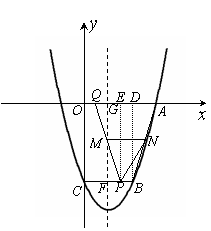 解:(1)∵二次函数
解:(1)∵二次函数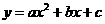 的图象经过点C(0,-3),
的图象经过点C(0,-3),
∴c =-3.
将点A(3,0),B(2,-3)代入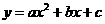 得
得
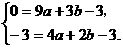
解得:a=1,b=-2.
∴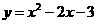 .-------------------2分
.-------------------2分
配方得: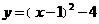 ,所以对称轴为x=1.-------------------3分
,所以对称轴为x=1.-------------------3分
(2) 由题意可知:BP= OQ=0.1t.
∵点B,点C的纵坐标相等,
∴BC∥OA.
过点B,点P作BD⊥OA,PE⊥OA,垂足分别为D,E.
要使四边形ABPQ为等腰梯形,只需PQ=AB.
即QE=AD=1.
又QE=OE-OQ=(2-0.1t)-0.1t=2-0.2t,
∴2-0.2t=1.
解得t=5.
即t=5秒时,四边形ABPQ为等腰梯形.-------------------6分
②设对称轴与BC,x轴的交点分别为F,G.
∵对称轴x=1是线段BC的垂直平分线,
∴BF=CF=OG=1.
又∵BP=OQ,
∴PF=QG.
又∵∠PMF=∠QMG,
∴△MFP≌△MGQ.
∴MF=MG.
∴点M为FG的中点 -------------------8分
∴S=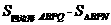 ,
,
= .
.
由
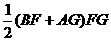 =
=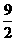 .
.
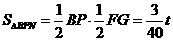 .
.
∴S=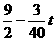 .-------------------10分
.-------------------10分
又BC=2,OA=3,
∴点P运动到点C时停止运动,需要20秒.
∴0<t≤20.
∴当t=20秒时,面积S有最小值3.------------------11分
22.(本题满分10分)
解: 探究 (1)①(1,0);②(-2,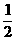 );-------------------------------2分
);-------------------------------2分
(2)过点A,D,B三点分别作x轴的垂线,垂足分别为
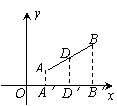
 ,
,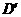 ,
,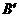 ,则
,则 ∥
∥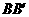 ∥
∥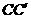 .-------------------------------3分
.-------------------------------3分
∵D为AB中点,由平行线分线段成比例定理得

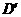 =
=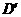
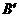 .
.
∴O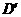 =
=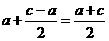 .
.
 即D点的横坐标是
即D点的横坐标是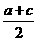 .------------------4分
.------------------4分
同理可得D点的纵坐标是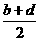 .
.
∴AB中点D的坐标为(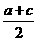 ,
,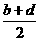 ).--------5分
).--------5分
归纳: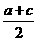 ,
,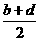 .-------------------------------6分
.-------------------------------6分
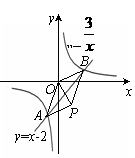
运用 ①由题意得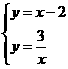

解得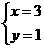
 或
或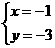
 .
.
∴即交点的坐标为A(-1,-3),B(3,1) .-------------8分
②以AB为对角线时,
由上面的结论知AB中点M的坐标为(1,-1) .
∵平行四边形对角线互相平分,
∴OM=OP,即M为OP的中点.
∴P点坐标为(2,-2) .---------------------------------9分
同理可得分别以OA,OB为对角线时,
点P坐标分别为(4,4) ,(-4,-4) .
∴满足条件的点P有三个,坐标分别是(2,-2) ,(4,4) ,(-4,-4) .------10分
21.(本题满分10分)
解:(1)由题意可知,
当x≤100时,购买一个需 元,故
元,故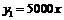 ;-------------------1分
;-------------------1分
当x≥100时,因为购买个数每增加一个,其价格减少10元,但售价不得低于3500元/个,所以x≤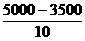 +100=250. ------------------------2分
+100=250. ------------------------2分
即100≤x≤250时,购买一个需5000-10(x-100)元,故y1=6000x-10x2;----------4分
当x>250时,购买一个需3500元,故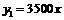 ; ----------------5分
; ----------------5分
所以,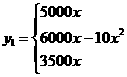
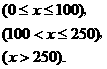
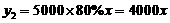 . -------------------------------7分
. -------------------------------7分
(2) 当0<x≤100时,y1=5000x≤500000<1400000;
当100<x≤250时,y1=6000x-10x2=-10(x-300)2+900000<1400000;
所以,由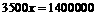 ,得
,得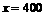 ; -------------------------------8分
; -------------------------------8分
由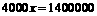 ,得
,得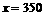 . -------------------------------9分
. -------------------------------9分
故选择甲商家,最多能购买400个路灯.-----------------------------10分
20. (本题满分10分)
(本题满分10分)
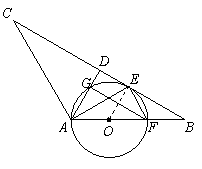
(1)证明:连接OE,------------------------------1分
∵AB=AC且D是BC中点,
∴AD⊥BC.
∵AE平分∠BAD,
∴∠BAE=∠DAE.------------------------------3分
∵OA=OE,
∴∠OAE=∠OEA.
∴∠OEA=∠DAE.
∴OE∥AD.
∴OE⊥BC.
∴BC是⊙O的切线.---------------------------6分
(2)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.----------------------------7分
∴∠EOB =60°.------------------------------8分
∴∠EAO =∠EAG =30°.-------------------9分
∴∠EFG =30°.------------------------------10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com