
题目列表(包括答案和解析)
6.下列说法中,错误的是
A.平行四边形的对角线互相平分 B.矩形的对角线互相垂直
C.菱形的对角线互相垂直平分 D.等腰梯形的对角线相等
5.在如图3所示的图形中,三角形的个数共有
A.1个 B.2个 C.3个 D.4个

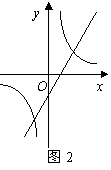
4.一次函数y=kx+b与反比例函数y=在同一直角坐标系中的大致图象如图2所示,则下列判断正确的是
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
3.不等式组的解集在数轴上表示正确的是

2.2010年3月,温家宝总理在2010年政府工作报告中指出,2009年在国际金融危机的强烈冲击下,我国国内生产总值仍达到33.5万亿元,比上年增长8.7%. 33.5万亿元这个数据用科学记数法表示为
A.33.5×l09 B.33.5×l012 C.3.35×l012 D.3.35×l013
1.- 的倒数是
A.-3 B.3 C.- D.
 ∴得到 c=4
∴得到 c=4
4a-2b+c=0
36a+6b+c=0------------------------------------------------------------------------------2分
解得a=-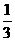 , b=
, b=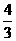 , c=4
, c=4
∴抛物线的解析式为y=-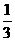 x
x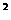 +
+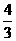 x+4---------------------------------------------------------3分
x+4---------------------------------------------------------3分
(或y=-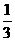 (x+2)(x-6)或y=-
(x+2)(x-6)或y=-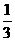 (x-2)
(x-2)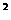 +
+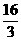 . )
. )
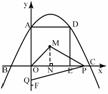 四边形OADE为正方形. --------------------------------------------------------------------------4分
四边形OADE为正方形. --------------------------------------------------------------------------4分
(2)根据题意可知OE=OA=4 OC=6 OB=OF=2
∴CE=2∴CO=FA=6
∵运动的时间为t∴CP=FQ=t
过M作MN⊥OE于N,则MN=2
当0≤t<2时,OP=6-t, OQ=2-t -------------------------------------------------------------------5分
∴S=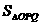 +
+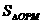 =
=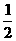 (6-t)×2+
(6-t)×2+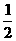 (6-t)(2- t)=
(6-t)(2- t)=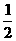 (6-t)(4- t)
(6-t)(4- t)
∴S = 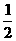 t
t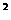 -5t+12. --------------------------------------------------------------------------------7分
-5t+12. --------------------------------------------------------------------------------7分
当t=2时,Q与O重合,点M、O、P、Q不能构成四边形.(不写也可)
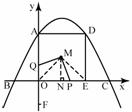 当2<t<6时,连接MO,ME则MO=ME且∠QOM=∠PEM=45
当2<t<6时,连接MO,ME则MO=ME且∠QOM=∠PEM=45 ---------------------------------8分
---------------------------------8分
∵FQ=CP=t,FO=CE=2
∴OQ=EP
∴△QOM≌△PEM
∴四边形OPMQ的面积S=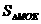 =
=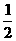 ×4×2=4------------------------------------------------10分
×4×2=4------------------------------------------------10分
综上所述,当0≤t<2时,S=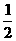 t
t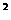 -5t+12;当2<t<6时,S=4
-5t+12;当2<t<6时,S=4
(3)存在N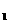 (1,5),N
(1,5),N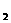 (5,
(5,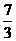 ),N
),N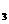 (2+
(2+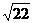 ,-2),N
,-2),N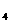 (2-
(2-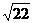 ,-2) -----------------------14分
,-2) -----------------------14分
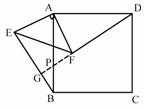 在正方形ABCD和等腰直角△AEF中
在正方形ABCD和等腰直角△AEF中
AD=AB,AF=AE,
∠BAD=∠EAF =90°
∴∠FAD=∠EAB
∴△FAD≌△EAB -----------------------------------------------------------------------------------2分
∴∠FDA=∠EBA DF=BE --------------------------------------------------------------------------3分
∵∠DPA=∠BPG, ∠ADP+∠DPA=90°
∴∠EBP+∠BPG=90°
∴∠DGB=90°
∴DF⊥BE --------------------------------------------------------------------------------------------5分
(2)改变. DF=kBE,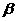 =180°-
=180°-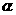 .---------------------------------------------------------------7分
.---------------------------------------------------------------7分
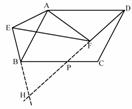
证法(一):延长DF交EB的延长线于点H
∵AD=kAB,AF=kAE
∴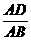 =k,
=k,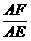 =k
=k
∴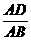 =
=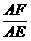
∵∠BAD=∠EAF =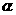
∴∠FAD=∠EAB
∴△FAD∽△EAB--------------------------------------------------------------------------------9分
∴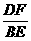 =
=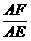 =k
=k
∴DF=kBE---------------------------------------------------------------------------------------10分
由△FAD∽△EAB得∠AFD=∠AEB
 ∵∠AFD+∠AFH=180
∵∠AFD+∠AFH=180
∴∠AEB+∠AFH=180°
∵四边形AEHF的内角和为360°,
∴∠EAF+∠EHF=180°
∵∠EAF=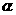 ,∠EHF=
,∠EHF=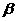
∴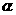 +
+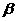 =180°∴
=180°∴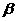 =180°-
=180°-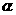 ----------------------------------------------------------12分
----------------------------------------------------------12分
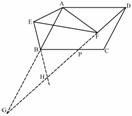 证法(二):DF=kBE的证法与证法(一)相同
证法(二):DF=kBE的证法与证法(一)相同
延长DF分别交EB、AB的延长线于点H、G.
由△FAD∽△EAB得∠ADF=∠ABE
∵∠ABE=∠GBH∴∠ADF=∠GBH
∵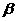 =∠BHF =∠GBH+∠G∴
=∠BHF =∠GBH+∠G∴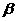 =∠ADF+∠G.
=∠ADF+∠G.
在△ADG中,∠BAD+∠ADF+∠G=180°,∠BAD=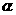
∴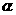 +
+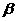 =180°∴
=180°∴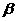 =180°-
=180°-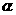 ----------------------------------------------------------12分
----------------------------------------------------------12分
证法(三):在平行四边形ABCD中AB∥CD可得到∠ABC+∠C=180°
∵∠EBA+∠ABC+∠CBH=180°∴∠C=∠EBA+∠CBH
在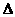 BHP、
BHP、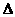 CDP中,由三角形内角和等于180°可得∠C+∠CDP=∠CBH+∠BHP
CDP中,由三角形内角和等于180°可得∠C+∠CDP=∠CBH+∠BHP
∴∠EBA+∠CBH+∠CDP=∠CBH+∠BHP
∴∠EBA+∠CDP=∠BHP
由△FAD∽△EAB得∠ADP=∠EBA
∴∠ADP+∠CDP=∠BHP即∠ADC=∠BHP
∵∠BAD+∠ADC=180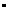 ,∠BAD=
,∠BAD=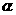 ,∠BHP=
,∠BHP=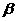
∴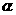 +
+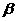 =180
=180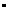 ∴
∴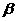 =180
=180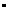 -
-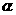 -----------------------------------------------------------12分
-----------------------------------------------------------12分
(有不同解法,参照以上给分点,只要正确均得分.)
24、解:(1)当0<x≤100且x为整数(或x取1,2,3,…,100)时,y=80;
当100<x≤500且x为整数(或x取101,102,…,500)时,y=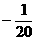 x+85;
x+85;
当x>500且x为整数(或x取501,502,503,…)时,y=60.------------4分
(注:自变量的取值范围只要连续即可)
(2)当x=200时,y=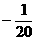 ×200+85=75
×200+85=75
∴所花的钱数为75×200=15000(元). ----------------------------------------------------6分
(3)当100<x≤500且x为整数时, y=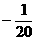 x+85
x+85
∴w=(y-45)x=(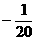 x+85-45)x
x+85-45)x
∴w=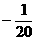 x
x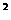 +40x--------------------------------------------------------------------------------8分
+40x--------------------------------------------------------------------------------8分
∴w=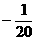 (x-400)
(x-400)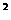 +8000-------------------------------------------------------------------9分
+8000-------------------------------------------------------------------9分
∵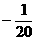 <0∴当x=400时, w最大,最大值为8000元
<0∴当x=400时, w最大,最大值为8000元
答:一次批发400件时所获利润最大,最大利润是8000元. ---------------------------10分
(2) 2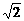 --------------------------------------------------------------------------------------------------5分
--------------------------------------------------------------------------------------------------5分
(3)AD与⊙M相切. -------------------------------------------------------------------------------------6分
证法一:过点M作MH⊥AD于H,连接MN, MA,则MN⊥AE且MN=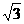
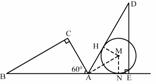 在Rt△AMN中,tan∠MAN=
在Rt△AMN中,tan∠MAN=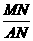 =
=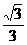 ∴∠MAN=30°---------------------------------------------7分
∴∠MAN=30°---------------------------------------------7分
∵∠DAE=∠BAC=60°
∴∠MAD=30°
∴∠MAN=∠MAD=30°
∴MH=MN(由△MHA≌△MNA或解Rt△AMH求得MH=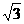 从而得MH=MN 亦可)------------9分
从而得MH=MN 亦可)------------9分
∴AD与⊙M相切. --------------------------------------------------------------------------------------10分
证法二:连接MA、ME、MD,则S =
=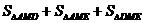 -----------------------------8分
-----------------------------8分
过M作MH⊥AD于H, MG⊥DE于G, 连接MN, 则MN⊥AE且MN=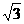 ,MG=1
,MG=1
∴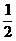 AC·BC=
AC·BC=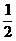 AD·MH+
AD·MH+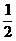 AE·MN+
AE·MN+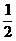 DE·MG
DE·MG
由此可以计算出MH =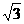 ∴MH=MN
---------------------------------------------------------------9分
∴MH=MN
---------------------------------------------------------------9分
∴AD与⊙M相切----------------------------------------------------------------------------------------10分
23.解:∵AF∥CE ∠ABC=60° ∴∠FAB=60°
∵∠FAD=15°∴∠DAB=45°--------------------------------------------------------------------------1分
∵∠DBE=60° ∠ABC=60°∴∠ABD=60°---------------------------------------------------------2分
过点D作DM⊥AB于点M,则有AM=DM
∵tan∠ABD=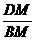 ∴tan60°=
∴tan60°=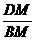 ∴DM=
∴DM=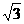 BM-----------------------------------------3分
BM-----------------------------------------3分
设BM=x则AM=DM=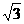 x
x
∵AB=AM+BM=8 ∴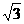 x + x=8-----------------------------------------------------------------------5分
x + x=8-----------------------------------------------------------------------5分
∴ x=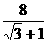 ≈3.0或 x=4(
≈3.0或 x=4(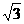 -1)
-1)
∴DM=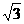 x ≈5或DM=
x ≈5或DM=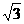 x=12-4
x=12-4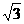 --------------------------------------------------------------7分
--------------------------------------------------------------7分
∵∠ABD=∠DBE=60° DE⊥BE DM⊥AB
∴DE=DM≈5(米)或DE=DM=12-4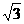 ≈5(米)(由△DEB≌△DMB得DE=DM同样正确或
≈5(米)(由△DEB≌△DMB得DE=DM同样正确或
根据BD=2BM=2x,由DE=BDsin60°=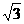 x≈5(米)亦正确)---------------------------------9分
x≈5(米)亦正确)---------------------------------9分
答这棵树约有5米高. --------------------------------------------------------------------------------10分
(不同解法,参照以上给分点,只要正确均得分.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com