
题目列表(包括答案和解析)
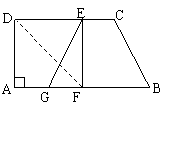
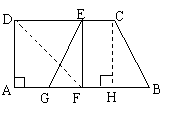
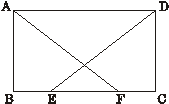
14.(2010年河南省南阳市中考模拟数学试题)如图,在直角梯形纸片ABCD中,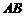 ∥
∥ ,
,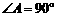 ,
,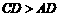 ,将纸片沿过点D的直线折叠
,将纸片沿过点D的直线折叠 ,使点A落在边CD上的点E处,折痕为
,使点A落在边CD上的点E处,折痕为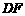 .连接EF并展开纸片.
.连接EF并展开纸片.
(1)求证:四边形ADEF是正方形;
(2)取线段AF的中点G,连接 ,如果
,如果 ,试说明四边形GBCE是等腰梯形.
,试说明四边形GBCE是等腰梯形.

答:(1)证明:
 ∵△ADF≌△EDF,
∵△ADF≌△EDF,
∴∠DEF=∠A=90°.
∵AB∥DC,
∴∠ADE=90°.
∴四边形ADEF为矩形.
又∵DA=DE,
∴ADEF为正方形.
(2 )过C作CH⊥AB,垂足为H,
)过C作CH⊥AB,垂足为H,
∵CE∥BG,CE≠BG,
∴EGBC是梯形.
∵CH⊥AB,
∴∠CHA=90°.
又∵∠CDA=∠DAH=90°,
∴ CDAH为矩形.
∴CD=AH.
又∵BG=CD,
∴BG=AH.
∴BH=AG.
又∵AG=GF,
∴GF=HB.
又∵∠EFG=∠CHB,EF=CH,
∴ △EFG≌△CHB.
∴EG=CB.
∴ EGBC为等腰梯形.
13.(2010年福建模拟)如图,在□ABCD中,E、F为BC
两点,且BE=CF,AF=DE.求证:
(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
证明:(1)∵BE=CF BF=BE+EF CE=CF+EF ∴BF=CE
又∵在平行四边形ABCD中,AB=CD
∴△ABF≌ △DEC(sss)
(2)由(1)知△ABF≌ △DEC ∴ ∠B=∠C
又∵在平行四边形ABCD中,AB∥CD
∴∠B+∠C=180° ∴∠C=90°
∴四边形ABCDJ是矩形.
12.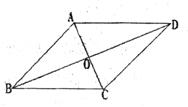 (2010年天水模拟)如图,在四边形ABCD中,AD∥BC,对角线AC与BD相交于点O,AC平分∠BA
(2010年天水模拟)如图,在四边形ABCD中,AD∥BC,对角线AC与BD相交于点O,AC平分∠BA D,请你再添一个什么条件?就能推出四边ABCD是菱形,并给出证明.
D,请你再添一个什么条件?就能推出四边ABCD是菱形,并给出证明.
答案:AD=BC
又∵ADBC
∴四边形ABCD为平行四边形
∴ABCD
又∵AC平分∠BAD
∴∠2=∠4 ∠1=∠3
∴∠3=∠2 ∠4=∠2
∴AD=CD
 ∴ABCD是菱形
∴ABCD是菱形
11. (2010年湖南模拟)如图,在等腰梯形ABCD中,已知∠B=44°,上底AD长为4,梯形的高为2,求梯形底边BC的长(精确到0.1).
(2010年湖南模拟)如图,在等腰梯形ABCD中,已知∠B=44°,上底AD长为4,梯形的高为2,求梯形底边BC的长(精确到0.1).
解:过A、D两点分别 作AE⊥BC,DF⊥BC,垂足为E、F.
作AE⊥BC,DF⊥BC,垂足为E、F.
∵梯形ABCD,∴AD∥BC,
又∵AE⊥BC,DF⊥BC,
∴AE∥DF,∴四边形AEFD是矩形.
∴AD=EF,AE=DF=2.
又∵等腰梯形ABCD,∴AB=CD,∠B=∠C,
∴△ABE≌△DCF,∴BE=CF.
∵在Rt△ABE中,cotB=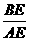 ,
,
∴BE=AEcotB=2cot44°,
∴BC=2BE+AD=4cot44°+4≈8.1.
答:梯形底边BC的长为8.1.
10.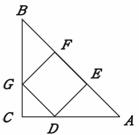 (2010年广东省中考拟)如图,在等腰Rt△ABC中,∠C=90°,
(2010年广东省中考拟)如图,在等腰Rt△ABC中,∠C=90°,
正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC=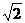 cm,求正方形DEFG的边长.
cm,求正方形DEFG的边长.
解:(1)∵ 等腰Rt△ABC中,∠ 90°,
90°,
∴ ∠A=∠B,
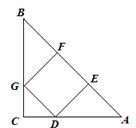 ∵ 四边形DEFG是正方形,
∵ 四边形DEFG是正方形,
∴ DE=GF, ∠DEA=∠GFB=90°,
∠DEA=∠GFB=90°,
∴ △ADE≌△BGF,
∴ AE=BF.
(2)∵ ∠DEA=90°,∠A=45°,
∴∠ADE=45°.
∴ AE=DE. 同理BF=GF.
∴ EF= AB=
AB=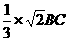 =
=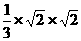 =
=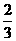 cm,
cm,
∴ 正方形DEFG的边长为 .
.
9.(2010年武汉市中考拟)已知:如图,已知:D是△ABC的边
AB上一点,CN∥AB,DN交AC于,若MA=MC,
求证:CD=AN.
证明:如图,因为 AB∥CN
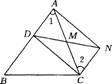 所以
所以 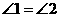 在
在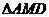 和
和 中
中
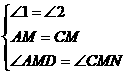
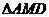 ≌
≌
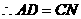

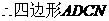 是平行四边形
是平行四边形
25. 解:(1)由题意知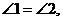
 又AB∥CD,得
又AB∥CD,得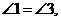 则
则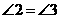 .故
.故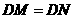 .
.
(2)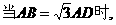
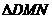 是等边三角形.
是等边三角形.
证明:∵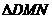 是等边三角形
是等边三角形
∴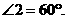 则
则
则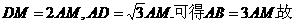
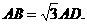
8.(2010年江西南昌一模)如图,将矩形ABCD沿MN折叠,使点B与点D重合.
 (1)求证:
(1)求证: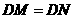 ;
;
(2)当 满足什么数量关系时,
满足什么数量关系时,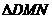
是等边三角形?并说明你的理由.
答案:
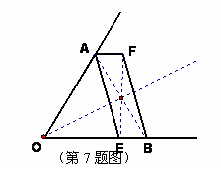
7.(2010年浙江杭州)(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF 是平
行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线.(保留作图痕迹,不要求写作法)
(2)如图2,在10×10的正方形网格中,点A(0,0)、B(5,0)、C(3,6)、D(-1,3),
①依次连结A、B、C、D四点得到四边形ABCD,四边形ABCD的形状是 .
②在x轴上找一点P,使得△PCD的周长最短(直接画出图形,不要求写作法);
此时,点P的坐标为 ,最短周长为 .

解:(1)如图所示;
(2)①等腰梯形;
②P( ,0)
,0)  (其中画图正确得2分)
(其中画图正确得2分)

6.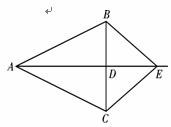 (2010年浙江永嘉)如图,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的延长线上取一点E,连结BE,CE. (1)求证:△ABE≌△ACE (2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
(2010年浙江永嘉)如图,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的延长线上取一点E,连结BE,CE. (1)求证:△ABE≌△ACE (2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
(1) 省略 (2) AE=AD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com