
题目列表(包括答案和解析)
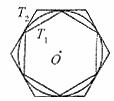
4.(2010年 中考模拟2)如图,有一个圆O和两个正六边形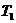 ,
,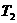 .
.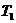 的6个顶点都在圆周上,
的6个顶点都在圆周上,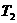 的6条边都和圆O相切(我们称
的6条边都和圆O相切(我们称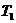 ,
,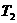 分别为圆O的内接正六边形和外切正六边形) .
分别为圆O的内接正六边形和外切正六边形) .
 (1)设
(1)设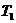 ,
,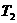 的边长分别为
的边长分别为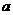 ,
,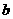 ,圆O的半径为
,圆O的半径为 ,求
,求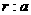 及
及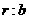 的值;
的值;
(2)求正六边形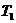 ,
,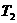 的面积比
的面积比 的值 .
的值 .
答案:(1)连接圆心O和T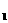 的6个顶点可得6个全等的正三角形 .
的6个顶点可得6个全等的正三角形 .
所以r∶a=1∶1;
连接圆心O和T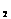 相邻的两个顶点,得以圆O半径为高的正三角形,
相邻的两个顶点,得以圆O半径为高的正三角形,
所以r∶b=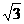 ∶2;
∶2;
(2) T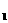 ∶T
∶T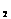 的连长比是
的连长比是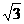 ∶2,所以S
∶2,所以S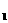 ∶S
∶S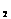 =
=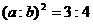
3. (2010年湖南模拟)如图 ,以△ACF的边AC为弦的圆交AF、CF于点B、E,连结BC,且满足AC2=CE·CF.求证:△ABC为等腰三角形.
(2010年湖南模拟)如图 ,以△ACF的边AC为弦的圆交AF、CF于点B、E,连结BC,且满足AC2=CE·CF.求证:△ABC为等腰三角形.
证明:连结AE.∵AC2=CE·CF,∴ 
又∵∠ACE=∠FCA.∴△ACE∽△FCA.
∴∠AEC=∠FAC. ∵ .
.
∴AC=BC,∴△ABC为等腰三角形.
2. (2010年湖南模拟)如图4,平行四边形ABCD中,以A为圆心,AB为半径的圆分别交AD、BC于F、G,延长B
(2010年湖南模拟)如图4,平行四边形ABCD中,以A为圆心,AB为半径的圆分别交AD、BC于F、G,延长B A交圆于E.求证:EF=FG.
A交圆于E.求证:EF=FG.
证明:连结AG.
∵A为圆心,∴AB=AG.
∴∠ABG=∠AGB.
∵四边形ABCD为平行四边形.
∴AD∥BC.∠AGB=∠DAG ,∠EAD=∠ABG.
,∠EAD=∠ABG.
∴∠DAG=∠EAD.
∴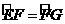 .
.
1.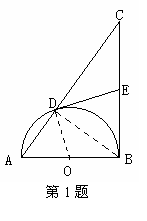 (2010年 河南模拟)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.
(2010年 河南模拟)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.
DE与半圆O相切吗?若相切,请给出证明;若不相切,请说明理由;
若AD、AB的长是方程x2-10x+24=0的两个根,求直角边BC的长.
解:(1)DE与半圆O相切.
证明: 连结OD、BD ∵AB是半圆O的直径
∴∠BDA=∠BDC=90° ∵在Rt△BDC中,E是BC边上的中点
∴DE=BE∴∠EBD=∠BDE∵OB=OD∴∠OBD=∠ODB
又∵∠ABC=∠OBD+∠EBD=90°
∴∠ODB+∠EBD=90°∴DE与半圆O相切.
(2)解:∵在Rt△ABC中,BD⊥AC
∴ Rt△ABD∽Rt△ABC
∴ = 即AB2=AD·AC∴ AC=
∵ AD、AB的长是方程x2-10x+24=0的两个根
∴ 解方程x2-10x+24=0得: x1=4 x2=6
∵ AD<AB ∴ AD=4 AB=6 ∴ AC=9
在Rt△ABC中,AB=6 AC=9
∴ BC===3
10.(2010年广州市中考六模)、如果点P在坐标轴上,以点P为圆心,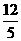 为半径的圆与直线
为半径的圆与直线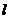 :
: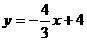 相切,则点P的坐标是
相切,则点P的坐标是
答案:(0,0)或(6,0)
9. (2010年广州市中考七模)、如右图,直角三角形ABC中,
(2010年广州市中考七模)、如右图,直角三角形ABC中,
∠C=90°,∠A=30°,点0在斜边AB上,半径为2的⊙O过
点B,切AC边于点D,交BC边于点E,则由线段CD,CE及
弧DE围成的隐影部分的面积为
答案: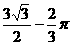
8.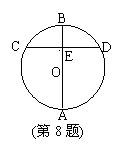 (2010年广州市中考六模)、如图:AB是⊙O的直径,弦CD⊥AB,
(2010年广州市中考六模)、如图:AB是⊙O的直径,弦CD⊥AB,
垂足为E,如果AB=10 , CD=8
, CD=8 ,那么AE的长为
,那么AE的长为
 .
.
答案:3.75
7.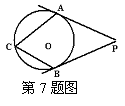 (2010年浙江永嘉)如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠P=50°,那么∠ACB等于____ .13、65°;
(2010年浙江永嘉)如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠P=50°,那么∠ACB等于____ .13、65°;
6.(2010年铁岭加速度辅导学校)如图,在矩形空地上铺4块扇形草地.若扇形的半径均为 米,圆心角均为
米,圆心角均为 ,则铺上的草地共有
平方米.
,则铺上的草地共有
平方米.


答案: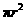
5.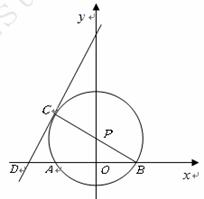 (2010年武汉市中考拟)如图,点
(2010年武汉市中考拟)如图,点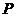 在
在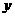 轴上,
轴上,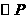 交
交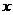 轴于
轴于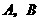 两点,连结
两点,连结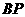 并延长交
并延长交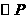 于
于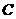 ,过点
,过点
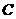 的直线
的直线 交
交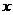 轴于
轴于 ,且
,且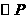 的半径为
的半径为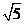 ,
,
 .若函数
.若函数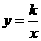 (x<0)的图象过C点,
(x<0)的图象过C点,
则k=___________.
答案:-4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com