
题目列表(包括答案和解析)
5.(2010年山东新泰)已知,在Rt△ABC中,∠C=90°,∠A=30°,CD是AB边的中线,若将△ABC沿CD折叠,使CA到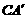 的位置,连结
的位置,连结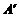 B.
B.
(1)求证:四边形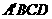 是菱形;
是菱形;
(2)若BC=2,试求四边形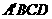 是菱形的面积
是菱形的面积 .
.
(1) ∵∠ACB=90°,∠A=30°.
∴BC=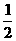 AB.
AB.
又CD是斜边AB的中线,
∴CD=AD=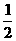 AB
=BD.
AB
=BD.
∴BC =AD= CD =BD, ∴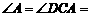 30°.
30°.
∵将△ABC沿CD折叠得△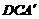 ,
,
∴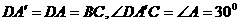 ,
,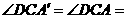 30°,
30°,
∴ 60°-30°=30°
60°-30°=30°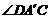 ,
,
∴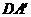 ∥CB.
∴四边形
∥CB.
∴四边形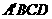 为菱形.
为菱形.
(2)∵BC=2,∴BD=2,易得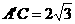 ,∴S=2
,∴S=2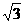 .
.
4.(2010年安徽省模拟)如图,在梯形ABCD中AD//BC,BD=CD,且∠ABC为锐角,若AD=4 ,BC=12, E为BC上的一点,当CE分别为何值时,四边形ABED是等腰梯形?直角梯形?写出你的结论,并加以证明。
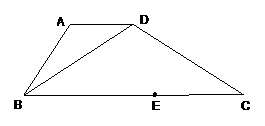
解:当CE=4时,四边形ABCD是等腰梯形
在BC上截取CE=AD,连接DE、AE.
又∵AD//BC, ∴四边形AECD是平行四边形
∴AE=CD=BD
∵BE=12-4=8>4, 即BE>AD
∴AB不平行于DE ∴四边形ABED是梯形
∵AE//CD, CD=BD, ∴∠AEB=∠C=∠DBE
在△ABE和△DEB中
AE=DB , ∠AEB=∠DBE, BE=EB
△ABE≌△DEB (SAS) , ∴AB=DE
∴四边形ABED 是等腰梯形
当CE=6,四边形ABED是直角梯形
在BC上取一点E,使得EC=BE= 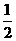 BC=6,连接DE,
BC=6,连接DE,
∵BD=CD,∴DE⊥BC
又∵BE≠AD,AD//BE, ∴AB不平行于DE
 ∴四边形ABDE是直角梯形
∴四边形ABDE是直角梯形
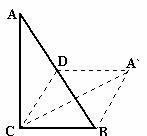
3. (2010年北京市朝阳区模拟)如图,在△ABC中,∠CAB、∠ABC
(2010年北京市朝阳区模拟)如图,在△ABC中,∠CAB、∠ABC
的平分线交于点D,DE∥AC交BC于点E,DF∥BC交AC于点F.
求证:四边形DECF为菱形.
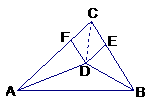 证法一:连结CD
证法一:连结CD
∵ DE∥AC,DF∥BC,
∴ 四边形DECF为平行四边形,
∵∠CAB、∠ABC的平分线交于点D
∴点D是△ABC的内心,
∴ CD平分∠ACB,即∠FCD=∠ECD,
∵DF∥BC
∴∠FDC=∠ECD,∴ ∠FCD=∠FDC
∴ FC=FD,
∴ 平行四边形DECF为菱形.
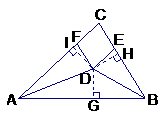 证法二:过D分别作DG⊥AB于G,DH⊥BC于H,DI⊥ACI.
证法二:过D分别作DG⊥AB于G,DH⊥BC于H,DI⊥ACI.
∵AD、BD分别平分∠CAB、∠ABC,
∴DI=DG,DG=DH.∴DH=DI.
∵DE∥AC,DF∥BC,
∴四边形DECF为平行四边形,
∴S□DECF=CE·DH =CF·DI,
∴CE=CF.
∴平行四边形DECF为菱形.
2.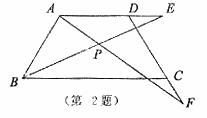 (2010年
中考模拟2)如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P .
(2010年
中考模拟2)如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P .
(1)求证:AF=BE;
(2)请你猜测∠BPF的度数,并证明你的结论 .
答案:
(1)∵BA=AD,∠BAE=∠ADF,AE=DF,
∴△BAE≌△ADF,∴BE=AF;
(2)猜想∠BPF=120° .
∵由(1)知△BAE≌△ADF,∴∠ABE=∠DAF .
∴∠BPF=∠ABE+∠BAP=∠BAE,而AD∥BC,∠C=∠ABC=60°,
∴∠BPF=120°
1.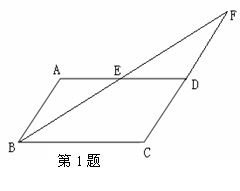 (2010 年河南模拟)在平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.
(2010 年河南模拟)在平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.
(1)求证: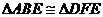 ;
;
(2)连接BD、AF,判断四边形ABDF的形状,
并证明你的结论
答案:(1)略,(2)平行四边形.
16.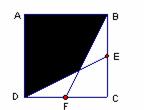 (2010年河南中考模拟题6)如图,正方形ABCD的边长为1cm,
(2010年河南中考模拟题6)如图,正方形ABCD的边长为1cm,
E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的
面积是
cm 2。
2。
答案: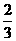
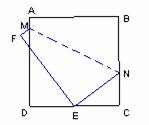
15.(2010年河南中考模拟题6)如图,将边长为8cm的正方形
ABCD折叠,使D落在BC边的中点E处,点A落在F处,折痕
为MN,则线段CN的长是
 。
。
答案:3cm
14.(2010年河南中考模拟题4)已知菱形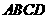 的对角线AC=6cm,BD=8cm,则菱形的边长是 cm.
的对角线AC=6cm,BD=8cm,则菱形的边长是 cm.
 答案:5
答案:5
13.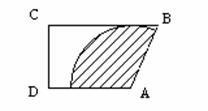 (2010年河南中考模拟题3)如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以A为圆心在梯形内画一个最大的扇形(图中阴影部分)的面积是 。
(2010年河南中考模拟题3)如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以A为圆心在梯形内画一个最大的扇形(图中阴影部分)的面积是 。
答案:4π
12.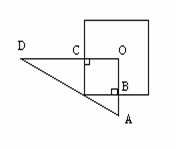 (2010年河南中考模拟题2)将正方形与直角三角形纸片按如右图所示方式叠放在一起,已知正方形的边长为 20cm ,点O为正方形的中心,AB=5cm,则CD的长为
。
(2010年河南中考模拟题2)将正方形与直角三角形纸片按如右图所示方式叠放在一起,已知正方形的边长为 20cm ,点O为正方形的中心,AB=5cm,则CD的长为
。
答案:20
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com