
题目列表(包括答案和解析)
14.(2010重庆市綦江中学模拟1)(10分)小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如右图:
(1)请你完成下面表示游戏一个回合所有可能出现
的结果的树状图;
(2)求一个回合能确定两人先下棋的概率.



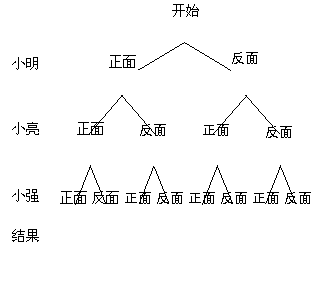
(2)由(1)中的树状图可知:P(确定两人先下棋)=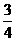 .
.
13.(10年广州市中考七模)、桌面上有15张扑克牌,甲、乙两人轮流取,每次最少取一张,最多取三张,谁取走最后一张谁就赢。
(1)这个游戏规则对于甲、乙两方公平吗?
(2)是先取者毕胜,还是后取者毕胜?有何致胜秘诀?
(3)若将上面的15张扑克换成n张(n是不小于4的正整数),情况有如何?
答案:(1)不公平
(2)是先取者赢,
 因为为了要取得最后一根,甲必须最后留下零根火柴给乙,故在最后一步之前的轮取中,甲不能留下1根或2根或3根,否则乙就可以全部取走而获胜。如果留下4根,则乙不能全取,则不管乙取几根(1或2或3),甲必能取得所有剩下的火柴而赢了游戏。同理,若桌上留有8根火柴让乙去取,则无论乙如何取,甲都可使这一次轮取後留下4根火柴,最后也一定是甲获胜。由上分析可知,甲只要使得桌面上的火柴数为4﹑8﹑12﹑16...等让乙去取,则甲必稳操胜券。因此若原先桌面上的火柴数为15,则甲应取3根。(∵15-3=12)
因为为了要取得最后一根,甲必须最后留下零根火柴给乙,故在最后一步之前的轮取中,甲不能留下1根或2根或3根,否则乙就可以全部取走而获胜。如果留下4根,则乙不能全取,则不管乙取几根(1或2或3),甲必能取得所有剩下的火柴而赢了游戏。同理,若桌上留有8根火柴让乙去取,则无论乙如何取,甲都可使这一次轮取後留下4根火柴,最后也一定是甲获胜。由上分析可知,甲只要使得桌面上的火柴数为4﹑8﹑12﹑16...等让乙去取,则甲必稳操胜券。因此若原先桌面上的火柴数为15,则甲应取3根。(∵15-3=12)
(3)还是先取者赢
12.(2010浙江杭州)在中央电视台第2套《购物街》栏目中,有一个精彩刺激的游戏――幸运大转盘,其规则如下:
①游戏工具是一个可绕轴心自由转动的圆形转盘,转盘按圆心角均匀划分为20等分,并在其边缘标记5、10、15、…、100共20个5的整数倍数,游戏时,选手可旋转转盘,待转盘停止时,指针所指的数即为本次游戏的得分;
②每个选手在旋转一次转盘后可视得分情况选择是否再旋转转盘一次,若只旋转一次,则以该次得分为本轮游戏的得分,若旋转两次则以两次得分之和为本轮游戏的得分;
③若某选手游戏得分超过100分,则称为“爆掉”,该选手本轮游戏裁定为“输”,在得分不超过100分的情况下,分数高者裁定为“赢”;
④遇到相同得分的情况,相同得分的选手重新游戏,直到分出输赢.
现有甲、乙两位选手进行游戏,请解答以下问题:
(1)甲已旋转转盘一次,得分65分,他选择再旋转一次,求他本轮游戏不被“爆掉”的概率.
(2)若甲一轮游戏最终得分为90分,乙第一次旋转转盘得分为85分,则乙还有可能赢吗?赢的概率是多少?
(3)若甲、乙两人交替进行游戏,现各旋转一次后甲得85分,乙得65分,你认为甲是否应选择旋转第二次?说明你的理由.
解:(1)甲可取5、10、15、20、25、30、35,
∴P(不爆掉)=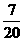
(2)乙有可能赢,
乙可取5、10、15,
P(乙赢)=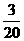
(3)甲选择不转第二次.
理由是:甲选择不转第二次,乙必须选择旋转第二次,
此时P(乙赢)=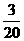 ,∴乙获胜的可能性较小.
,∴乙获胜的可能性较小.
或“甲若选择转第二次,P(甲爆掉)=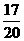 ,∴甲输而乙获胜的可能性较大.”
,∴甲输而乙获胜的可能性较大.”
(叙述的理由合理即可)
11.(2010山东新泰)小明和小刚做一个“配紫色”的游戏,用如图所示的两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色。规则如下:分别旋转两个转盘,若其中一个转盘出现了红色,另一个转盘出现了蓝色,则可配成紫色,此时小刚得1分,否则小明得1分.这个游戏对双方公平吗?请说明理由.若你认为不公平,如何修改游戏规则,才能够使游戏对双方公平?


答案:游戏对双方不公平.
游戏结果分析如下:“√”表示配成紫色,“×”表示不能够配成紫色.
|
|
红 |
蓝 |
黄 |
|
红 |
× |
√ |
× |
|
蓝 |
√ |
× |
× |
因为P(配成紫色)=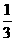 ,P(配不成紫色)=
,P(配不成紫色)=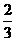 ,所以小刚得分:
,所以小刚得分: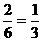 ,小明得分:
,小明得分: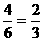 .
.
所以游戏对双方不公平.
修改规则为:若配成紫色,小刚得2分,否则小明得1分,此游戏对双方才公平 .(方法不唯一)
.(方法不唯一)
10.(江西南昌一模)小李和小王设计了A、B两种游戏:
游戏A的规则:用四张数字分别为2、3、4、5的扑克牌,将扑克牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小李获胜;若两数字之和为奇数,则小王获胜.
游戏B的规则:用四张数字分别为5、6、6、8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小李先随机抽出一张牌,抽出的牌不放回,小王从剩下的牌中随机抽出一张牌.若小李抽出的牌面上的数字比小王的大,则小李获胜;否则,小王获胜.
请你帮小王选择其中一种游戏,使他获胜的可能性较大,说明理由.
答案:A游戏:小王获胜的概率为 ,B游戏:小王获胜的概率为 ,所以小王选择B游戏。
9.(2010年武汉市中考拟)武汉某中学2009年元旦晚会上,主持人安排了抽奖活动.具体方法是:设置如下表所示的翻板,每次抽奖翻开一个数字,数字背面写有所中奖品或新年祝词.
|
1 |
2 |
3 |
|
4 |
5 |
6 |
|
7 |
8 |
9 |
|
奖MP4一个 |
万事如意 |
学业进步 |
|
身体健康 |
新年快乐 |
奖MP3一个 |
|
奖笔记本一个 |
奖钢笔一支 |
心想事成 |
(1)主持人想知道“第一个人抽奖中奖”的概率,而且觉得翻版牌太麻烦,请你设计一个简便的模拟抽奖方法,并估计“第一个人抽奖中奖”的概率.
(2)若晚会开始前给每名入场的学生发一张入场券,其中有100张后标有“新年快乐”.晚会进行中主持人任意邀请台下50名同学上台合唱“同一首歌”,并宣布这50名同学的入场券后标有“新年快乐”的参与抽奖,结果有4人中奖,中奖率为40%,请估计参加本次晚会的学生人数.
答案:(1)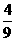 (2)500
(2)500
8.(2010年杭州月考) 在一个口袋中有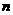 个小球,其中两个是白球,其余为红球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,从袋中随机地取出一个球,它是红球的概率是
个小球,其中两个是白球,其余为红球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,从袋中随机地取出一个球,它是红球的概率是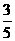 .
.
(1)求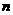 的值;
的值;
(2)把这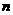 个球中的两个标号为1,其余分别标号为2,3,…,
个球中的两个标号为1,其余分别标号为2,3,…,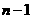 ,随机地取出一个小球后不放回,再随机地取出一个小球,求第二次取出小球标号大于第一次取出小球标号的概率。
,随机地取出一个小球后不放回,再随机地取出一个小球,求第二次取出小球标号大于第一次取出小球标号的概率。
答案:(1)依题意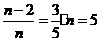 .
.
(2)当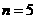 时,这5个球两个标号为1,其余标号分别为2,3,4.
时,这5个球两个标号为1,其余标号分别为2,3,4.
两次取球的小球标号出现的所有可能的结果如下表:
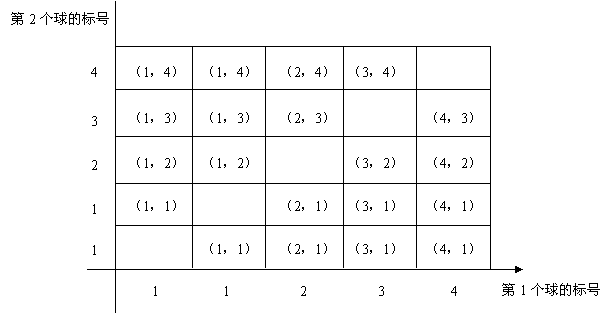
 由上表知所求概率为
由上表知所求概率为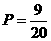 .
.
7.(2010年西湖区月考)现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数,另一个纸箱内4个小球上分别写有5、6、7、8这4个数,甲、乙两人商定了一个游戏,规则是 :从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
:从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;
(2)你认为这个游戏公平吗?为什么?若不公平,请你修改得分规则,使游戏对双方公平.
答案:(1)所有可能出现的结果如下:

(注:也可用树状图,略)
共有16种情况,且每种情况出现的可能性相同,其中,乘积是2的倍数的有12种,乘积是3的倍数的有7种.
∴P(两数乘积是2的倍数)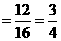
P(两数乘积是3的倍数)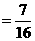
(2)游戏不公平.
∵甲每次游戏的平均得分为: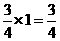 (分)
(分)
乙每次游戏的平均得分为: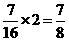 (分)
(分)
∵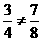
∴游戏不公平
修改得分规则为:把两个小球上的数字相乘,若得到的积是2的倍数,则甲得7分,若得到的积是3的倍数,则乙得12分.
6.(2010年西湖区月考)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2 个,黄球有1个,蓝球有1个. 现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
答案:树状图(略)
P(小明)=3/8 P(小亮)=5/8 所以不公平
5.(2010福建模拟)不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为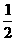 .
.
(1)求袋中蓝球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法,求两次摸到都是白球的概率.
(1)设袋中蓝球的个数是x个,根据题意有:
∴ x=1
经检验x=1是原方程的解
∴袋中蓝球的个数是1个.
(2)树状图为: 开始
 白1
白2
黄
蓝
白1
白2
黄
蓝
白2 黄 蓝 白1 黄 蓝 白1 白2 蓝 白1 白2 黄
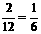 共有12种可能结果.
共有12种可能结果.
∴两次摸到都是白球的概率P(白)=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com