
题目列表(包括答案和解析)
8.如图8-54,已知在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
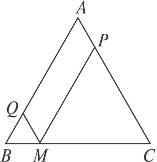
图8-54
(1)求四边形AQMP的周长;
(2)写出图中的两对相似三角形(不需证明);
(3)M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由.
(1)答案:2a.
提示:根据平行的性质可以得到平行四边形和两个等腰三角形,由对边和腰相等,四边形的周长等于△ABC的两腰之和.
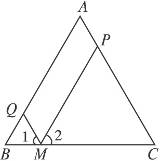
∵PM∥AB,QM∥AC,
∴四边形AQMP为平行四边形,
且∠1=∠C,∠2=∠B.
又∵AB=AC=a,
∴∠B=∠C.
∴∠1=∠B=∠C=∠2.
∴QB=QM,PM=PC.
∴四边形AQMP的周长为
AQ+QM+MP+PA=AQ+QB+PC+PA=AB+AC=2a.
(2)答案:△BQM∽△MPC∽△BAC.
(3)答案:当M为底边BC的中点时,四边形AQMP为菱形.
提示:四边形AQMP已是平行四边形,要使之为菱形,则需有一组邻边相等.
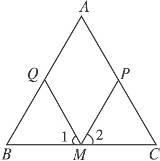
理由:∵M为底边BC的中点,
∴BM=CM.
由(1)知∠B=∠C,∠1=∠2,
∴△BQM≌△CMP.
∴PM=QM.
由(1)四边形AQMP为平行四边形,
∴四边形AQMP为菱形.
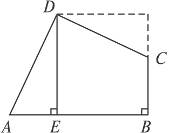
7.如图8-53,在四边形ABCD中,∠ADC=∠B=90°,DE⊥AB,垂足为E,且DE=EB=5,请用割补(旋转图形)的方法求四边形ABCD的面积.
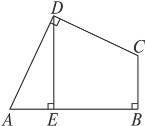
图8-53
答案:S=25.
提示:如图,把△ADE绕点D逆时针旋转90°后,得到的图形为边长是5的正方形,面积为25.
6.如图8-52,△ABC是等边三角形,P是△ABC内一点,PE∥AC交AB于点E,PF∥AB交BC于点F,PD∥BC交AC于点D.已知△ABC的周长是12 cm,则PD+PE+PF=______________ cm.
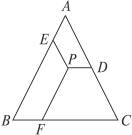
图8-52
答案:4
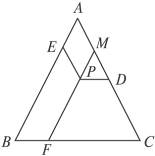
提示:延长FP,交AC于M,可得到平行四边形AMPE和等边三角形MPD,所以三条线段的和为等边三角形的边长,即PE=AM,PD=MD,PF=CD,所以PD+PE+PF=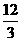 =4.
=4.
5.如图8-51,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的中位线长是________________.
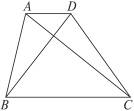
图8-51
答案:7.5
提示:如图,平移对角线形成直角三角形,且AC=12,BD=9,根据勾股定理,求BE=15,即上下底的和为15,又因为中位线长为上下底和的一半,所以为7.5.
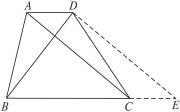
4.(2010四川遂宁中考)如图8-50,在梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形折叠,点A恰好与点D重合,BE为折痕,那么AD的长度为_______________.
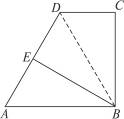
图8-50
答案:30
提示:利用折叠前后相等线段和勾股定理,AB=DB,又∵∠C=90°,可求出DC=7.
过D作DF⊥AB,垂足为F,利用勾股定理可求AD=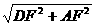 =
=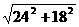 =30.
=30.
3.如图8-49,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于________________.
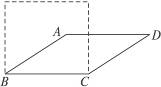
图8-49
答案:30°
提示:使其面积为矩形面积的一半,由于两个四边形的底相等,所以平行四边形的高为矩形宽的一半,即高为CD的一半,在直角三角形中一条直角边等于斜边的一半,则它所对的锐角为30°.
2.如图8-48,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是________________.
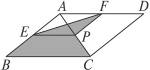
图8-48
答案:2.5
提示:易证四边形AEPF也是菱形,△PEF与△AEP同底等高,所以,S△PEF=S△AEP,S阴影=S△ABC=菱形面积的一半,菱形面积=对角线乘积的一半=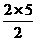 =5,所以S阴影=2.5.
=5,所以S阴影=2.5.
1.如图8-47,在△ABC中,AD⊥BC于D,E、F分别是AB、AC的中点,当△ABC满足条件__________时,AEDF是菱形.
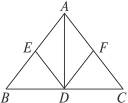
图8-47
答案:AB=AC
提示:如果是等腰三角形,AD⊥BC于D,依据等腰三角形三线合一,则D为中点,又E、F分别是AB、AC的中点,所以DE∥AC,DF∥AB.四边形是平行四边形且有一组邻边相等,所以为菱形,因此添加AB=AC.
11.图7-28是某次海战中敌我双方舰艇对峙示意图,对我方潜艇来说.
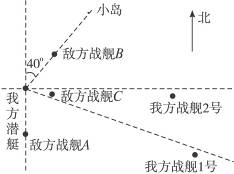
图7-28
(1)北偏东40°的方向上约有哪些目标?要确定敌舰B的位置,还需要什么数据?
(2)距我方潜艇图上距离1 cm处的敌舰有哪几艘?
(3)要确定每艘敌舰的位置,各需要几个数据?
(4)在图中北偏西30°的方向上,距我方潜艇1.5 cm处有一艘渔船,请在图中找到它的位置.
(5)如果你们分别是我方战舰1、2号上的作战参谋,请确定敌战舰的位置.
答案:(1)2a-8<0,2-a<0,a=3关于x轴对称,横坐标不变,纵坐标相反,点P到x轴的距离是其纵坐标的绝对值,P到y轴的距离是其横坐标的绝对值,北偏东40°的方向上有小岛、敌方战舰B.要确定敌舰B的位置,还需要与我方潜艇的距离;
(2)距我方潜艇图上距离1 cm处的敌舰有敌方战舰B、敌方战舰A;
(3)要确定每艘敌舰的位置,各需要两个数据;
(4)略;
(5)敌方战舰B在我方潜艇北偏东40°方向上距离1 cm,敌方战舰C在我方潜艇南偏东75°方向上距离0.6 cm,敌方战舰A在我方潜艇正南40°方向上距离1 cm.
5.(3,3).
答案:略.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com