
题目列表(包括答案和解析)
1 .(2010年广州市中考六模)、吕晓同学想利用树影的长测量校园内一棵大树的高度,他在某一时刻测得一棵小树的高
.(2010年广州市中考六模)、吕晓同学想利用树影的长测量校园内一棵大树的高度,他在某一时刻测得一棵小树的高 为1.5米,其影长为1.2米,同时,他测得这棵大树的影长为3米,则这棵大树的实际高度为 米.
为1.5米,其影长为1.2米,同时,他测得这棵大树的影长为3米,则这棵大树的实际高度为 米.
 答案:8
答案:8
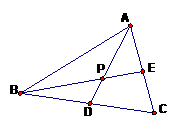
2.(2010年三亚市月考)如图,在△ABC中,∠C=90°,AD平分∠BAC
交BC于点D,BD︰DC=2︰1,BC=7 .8cm,则D到AB的距离
cm.
.8cm,则D到AB的距离
cm.
 答案 2
答案 2 .6
.6
3.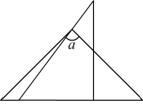 一副三角板如图叠放在一起,则图中∠α的度数为( )
一副三角板如图叠放在一起,则图中∠α的度数为( )
A.75° B.60°
C.65° D.55°
答案:A
2.(2010年浙江永嘉) 已知
已知 的三边长分别为5,13,12,则
的三边长分别为5,13,12,则 的面积
的面积 为( )
为( )
A.30
B.60 C.78 D.不 能确定
能确定
答案:A
1.(2010年广州市中考六模)已知D 、E为△ABC的边AB、AC上的两点,且AB=8,AC=6,AD=4,AE=3,则
、E为△ABC的边AB、AC上的两点,且AB=8,AC=6,AD=4,AE=3,则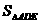 ∶
∶ =( )
=( )
A.1∶2 B.1∶4 C.1∶3 D.2∶5
答案:B
18.(2010年 中考模拟2)如图,已知线段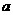 .
.
(1)只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC,以AB和BC分别为两条直角边,使AB=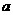 ,BC=
,BC=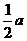 (要求保留作图痕迹,不必写出作法);
(要求保留作图痕迹,不必写出作法);
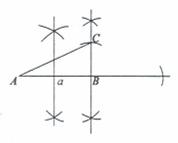
(2)若在(1)作出的RtΔABC中,AB=4cm,求AC边上的高 .

 答案:
答案:
(1)作图如 右,
右, 即为所求的直角三角形;
即为所求的直角三角形;
(2)由勾股定理得,AC=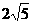 cm,
cm,
设斜边AC上的高为h, 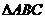 面积等于
面积等于
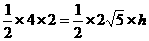 ,所以
,所以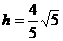
17.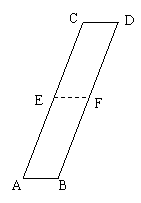 (2010年广西桂林适应训练)、如图,平行四边形纸条ABCD中,E、F分别是AD、BC的中点。将纸条的下半部分平行四边形ABFE沿EF翻折,得到一个V字形图案.
(2010年广西桂林适应训练)、如图,平行四边形纸条ABCD中,E、F分别是AD、BC的中点。将纸条的下半部分平行四边形ABFE沿EF翻折,得到一个V字形图案.
(1)请在原图中画出翻折后的平行四边形A´B´FE;(用尺规作图,不写画法,保留作图痕迹)
(2)已知∠A=65°,求∠B´FC的度数.
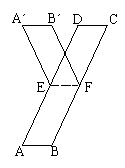 答案:(1)画出正确的图形(见右图)。
答案:(1)画出正确的图形(见右图)。
(2)∵四边ABEF是平行四边行
∴∠EFB=∠A=65°
∵四边形A´B´FE是由四边形ABFE翻折得到,
∴∠B´FE=∠EFB=65°
∴∠B´FC=180°-∠B´FE -∠EFB=50°
16.(2010年广州市中考七模)、在平面上有且只有四个点,这四个点有一个独特的性质:每两点之间的距离有且只有两种长度,例如正方形ABCD四个顶点A,B,C,D,有AB=BC=CD=DA,AC=BD,请画 出具有这种独特性质的另外四种不同的图形,并标明相等的线段。
出具有这种独特性质的另外四种不同的图形,并标明相等的线段。
答案:存在这些图形:1、一顶角为60度的菱形;2、正方形
;3、一个正三角形+ 顶角150度的等腰三角形构成的四边行(等腰三角形的底为正三角形的边)
;4、一个等腰三角形+内部一点,使得该点到3个顶点的距离均等于底边;5、一内角为72度且上底等于腰的等腰梯形 ;6、正三角形+心
顶角150度的等腰三角形构成的四边行(等腰三角形的底为正三角形的边)
;4、一个等腰三角形+内部一点,使得该点到3个顶点的距离均等于底边;5、一内角为72度且上底等于腰的等腰梯形 ;6、正三角形+心
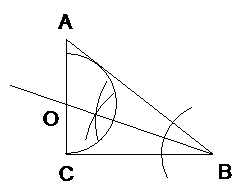
15.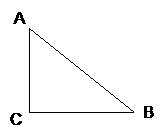 (2010年广州市中考六模)、如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.请你用直尺圆规画出来(要求用直尺和圆规作图,保留作图痕迹,不要求写作法).
(2010年广州市中考六模)、如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.请你用直尺圆规画出来(要求用直尺和圆规作图,保留作图痕迹,不要求写作法).
答案: 如图所示
如图所示
14.(济宁师专附中一模)如图,小刚家、王老师家和学校在 一条直路上,小刚与王老师家相距3.5千米,王老师家与学校相距0.5千米.近来,小刚父母出差,如果王老师骑自行车到小刚家接小刚上学,就比平时走路上班多用24分钟.已知骑自行车的速度是步行速度的3倍.
一条直路上,小刚与王老师家相距3.5千米,王老师家与学校相距0.5千米.近来,小刚父母出差,如果王老师骑自行车到小刚家接小刚上学,就比平时走路上班多用24分钟.已知骑自行车的速度是步行速度的3倍.
(1)问:王老师骑自行车的速度是多少千米/小时?
(2)为了节约时间,王老师与小刚 约定每天7:35从家里同时出发,小刚走路,王老师骑车,遇到小刚后,立即搭小刚到校.如果小刚和王老师走路的速度一样,王老师骑车的速度不变,请问他们能否在8:00钟前赶到学校?说明理由.
约定每天7:35从家里同时出发,小刚走路,王老师骑车,遇到小刚后,立即搭小刚到校.如果小刚和王老师走路的速度一样,王老师骑车的速度不变,请问他们能否在8:00钟前赶到学校?说明理由.
|

答案:解:(!)设王老师骑自行车的速度是x千米/小时,由题意得
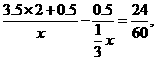 解得x=15,经检验知x=15是原方程的解且符合题意,所以王老师骑自行车的速度是15千米/小时.
解得x=15,经检验知x=15是原方程的解且符合题意,所以王老师骑自行车的速度是15千米/小时.
(2)答: 能在8:00钟前赶到学校,设王老师与小刚相遇用了y小时,相遇后小刚到校用了z小时,依题意得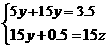 ,解得
,解得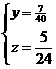 ,由
,由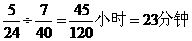 <25分钟,所以他们能在8:00钟前赶到学校.
<25分钟,所以他们能在8:00钟前赶到学校.
13.(黑龙江一模)某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
|
|
A型利润 |
B型利润 |
|
甲店 |
200 |
170 |
|
乙店 |
160 |
150 |
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到 最大?
最大?
答案:依题意,甲店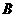 型产品有
型产品有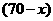 件,乙店
件,乙店 型有
型有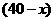 件,
件,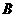 型有
型有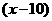 件,则
件,则
(1)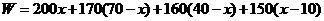
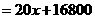 .
.
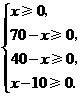 解得
解得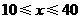 .
.
(2)由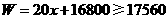 ,
,
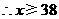 .
.
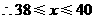 ,
,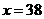 ,39,40.
,39,40.
 有三种不同的分配方案.
有三种不同的分配方案.
①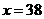 时,甲店
时,甲店 型38件,
型38件,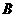 型32件,乙店
型32件,乙店 型2件,
型2件,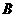 型28件.
型28件.
② 时,甲店
时,甲店 型39件,
型39件,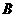 型31件,乙店
型31件,乙店 型1件,
型1件,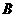 型29件.
型29件.
③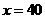 时,甲店
时,甲店 型40件,
型40件,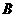 型30件,乙店
型30件,乙店 型0件,
型0件,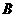 型30件.
型30件.
(3)依题意:
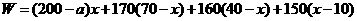
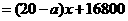 .
.
①当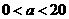 时,
时,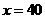 ,即甲店
,即甲店 型40件,
型40件,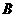 型30件,乙店
型30件,乙店 型0件,
型0件,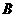 型30件,能使总利润达到最大.
型30件,能使总利润达到最大.
②当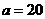 时,
时,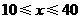 ,符合题意的各种方案,使总利润都一样.③当
,符合题意的各种方案,使总利润都一样.③当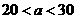 时,
时,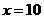 ,即甲店
,即甲店 型10件,
型10件,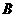 型60件,乙店
型60件,乙店 型30件,
型30件,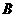 型0件,能使总利润达到最大.
型0件,能使总利润达到最大.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com