
题目列表(包括答案和解析)
10.(2010年黑龙江一模)如图,D是AB上一点,DF交AC于点E,AE=EC,CF∥AB.
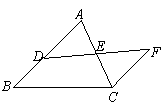 求证:AD=CF.
求证:AD=CF.
证明: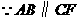 ,
,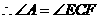 .
.
又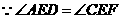 ,
,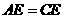 ,
,
 .
.
 .
.
9. (2010年广西桂林适应训练)已知:如图点
(2010年广西桂林适应训练)已知:如图点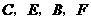 在同一直线上,
在同一直线上,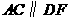 ,
, ,CE=BF.求证:AB‖DE .
,CE=BF.求证:AB‖DE .
证明:∵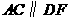
∴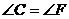
∵CE=BF
∴CE+BE=BF+BE
∴BC=EF
∵AC=DF
∴△ACB≌△DFE
∴
∴AB∥DE
8. (10年广州市中考六模)、如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离AH始终保持与AB长相等,问在E、F移动过程中:
(10年广州市中考六模)、如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离AH始终保持与AB长相等,问在E、F移动过程中:
(1)求证:∠EAF = 45o ;
(2)△ECF的周长是否有变化?请说明理由.
答案:
(1) 得到∠AHE=90o,Rt△ABE≌Rt△ABE
(2) 得到∠BAE=∠HAE
(3) 同理:∠DAF=∠HAF
(4) 得到2∠EAF=∠BAD,∠EAF=45o
(2)△ECF的周长是否有变化?请说明理由
(1) 不变

(2) 由Rt△ABE≌Rt△ABE得到BE=HE
(3) 同理:DF=HF 
(4) C△ABC = CE+CF+EF=CE+CF+BE+DF=2AB
7.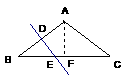 (2010年广州市中考六模)、王叔叔家有一块等腰三角形的菜地,腰长为40米,一
(2010年广州市中考六模)、王叔叔家有一块等腰三角形的菜地,腰长为40米,一 条笔直的水渠从菜地穿过,这条水渠恰好垂直平分等腰三角形的一腰,水渠穿过菜地部分的长为15米(水渠的宽不计),请你计算这块等腰三角形菜地的面积.
条笔直的水渠从菜地穿过,这条水渠恰好垂直平分等腰三角形的一腰,水渠穿过菜地部分的长为15米(水渠的宽不计),请你计算这块等腰三角形菜地的面积.
答案:情况1:锐角
(1)证明△ADE∽△AFC 得到CF=24 S△ABC=480
情况2:钝角
(2)证明△BDE∽△BFA 得 到AF=24,BC=64 S△ABC=768
到AF=24,BC=64 S△ABC=768
6.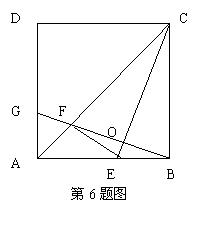 (2010年
(2010年 三亚市月考)如图,在正方形ABCD中,E是AB边上任意一点,BG⊥CE,垂足为点O,交AC于点F,交AD于点G。
三亚市月考)如图,在正方形ABCD中,E是AB边上任意一点,BG⊥CE,垂足为点O,交AC于点F,交AD于点G。
(1) 证明:BE=AG ;
(2) 点E位于什么位置时,∠AEF=∠CEB,说明 理由.
理由.
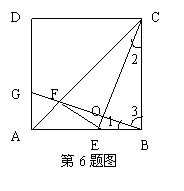
解(1)证明:∵四边形ABCD是正方形
∴∠ABC=∠BAD=90°,∴∠1+∠3=90°,
∵BG⊥CE,∴∠BOC=90°∴∠2+∠3=90°,
∴∠1=∠2 ………………………2分
在△GAB和△EBC中,
∵∠GAB=∠EBC=90°,AB=BC,∠1=∠2
∴△GAB≌△EBC (ASA) …………4分
 ∴AG=BE ………………………… 5分
∴AG=BE ………………………… 5分
(2)解:当点E位于线段AB中点时,∠AEF=∠CEB …… 6分
理由如下:若当点E位于线段AB中点时,则AE=BE,
由(1)可知,AG=BE ∴AG=AE …………………… 7分
∵四边形ABCD是正方形,∴∠GAF=∠EAF=45°… 8分
又∵AF=AF,∴△GAF≌△EAF (SAS)
∴∠AGF=∠AEF ………………………………………10分
由(1)知,△GAB≌△EBC ∴∠AGF=∠CEB,
∴∠AEF=∠CEB ………………………………… 11分
5.(2010年 湖里区 二次适应性考试)已知:如图,直径为 的
的
 与
与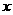 轴交于点O、A,点
轴交于点O、A,点 把弧OA分为三等分,连结
把弧OA分为三等分,连结 并延长交
并延长交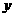 轴于D(0,3).
轴于D(0,3).
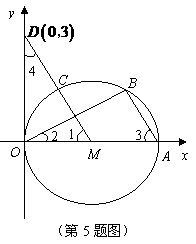
(1)求证: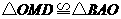 ;(2)若直线
;(2)若直线 :
: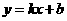 把
把 的面积分为二等分,
的面积分为二等分,
求证: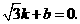
答案:证明:
(1)  连接
连接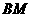 ,∵OA是直径,且
,∵OA是直径,且 把弧OA三等分,
把弧OA三等分,
∴ ,
,
又∵ ,∴
,∴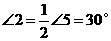 ,
,
又∵OA为 直
直 径,∴
径,∴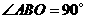 ,
,
∴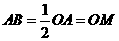 ,
,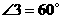 ,
,
∴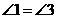 ,
,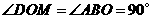 ,
,
在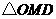 和
和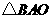 中,
中,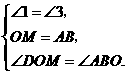
∴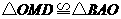 (ASA)
(ASA)

(2)若直线 把
把 的面积分为二等份,
的面积分为二等份,
则直线
 必过圆心
必过圆心 ,
,
∵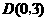 ,
,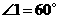 ,
,
∴在Rt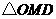 中,
中,
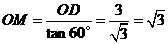 ,
,
∴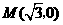 ,
,
把 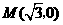 代入
代入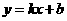 得:
得: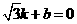
4.(2010年赤峰市中考模拟)如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,AF
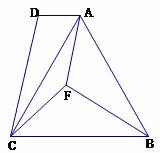 ∥DC,连接AC、CF,求证:CA是∠DCF的平分线.
∥DC,连接AC、CF,求证:CA是∠DCF的平分线.
答案:
证明∵AB=BC,BF是∠ABC的平分线, ∴∠ABF=∠CBF,又∵BF=BF, ∴△ABF≌△CBF。∴AF=CF。∴∠ACF=∠CAF.
又∵AF∥DC,∴∠ACF=∠ACD。
 ∴CA是∠DCF的平分线。
∴CA是∠DCF的平分线。
3.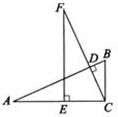 (2010年北京市中考模拟)已知:如图,在△ABC中,∠ACB=
(2010年北京市中考模拟)已知:如图,在△ABC中,∠ACB= ,
,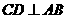 于点D,点E 在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F .
于点D,点E 在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F .
求证:AB=FC
答案:证明:∵ 于点
于点 ,
,
∴ 。∴
。∴ 。
。
又∵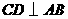 于点
于点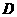 ,∴
,∴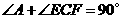 。∴
。∴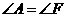 .
.
 在
在 和
和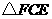 中,
中,
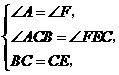
∴
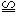
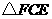 。
。
∴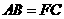 。
。
2.(2010年中考模拟2)如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F
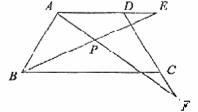 分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P .
分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P .
(1)求证:AF=BE;
(2)请你猜测∠BPF的度数,并证明你的结论 .
答案:
(1)∵BA=AD,∠BAE=∠ADF,AE=DF,
∴△BAE≌△ADF,∴BE=AF;
(2)猜想∠BPF=120° .
∵由(1)知△BAE≌△ADF,∴∠ABE=∠DAF .
∴∠BPF=∠ABE+∠BAP=∠BAE,而AD∥BC,∠C=∠ABC=60°,
∴∠BPF=120
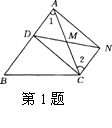
1.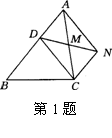 (2010年 河南模拟)已知:如图,已知:D是△ABC的边AB上一点,CN∥AB,DN交AC于,若MA=MC,
(2010年 河南模拟)已知:如图,已知:D是△ABC的边AB上一点,CN∥AB,DN交AC于,若MA=MC,
求证:CD=AN.
证明:如图,因为 AB∥CN
所以
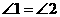 在
在 和
和 中
中
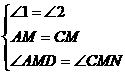
 ≌
≌
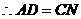
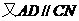
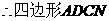 是平行四边形
是平行四边形
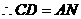
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com