
题目列表(包括答案和解析)
11.有一个角是30°的直角三角形,斜边为1 cm,则斜边上的高为
A.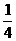 cm
B.
cm
B.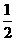 cm
cm
C.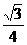 cm
D.
cm
D.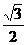 cm
cm
答案:C
提示:直角三角形中30°角所对的边等于斜边的一半,求出两直角边再利用面积或射影定理.
10.在Rt△ABC中, ∠C=90°,已知tanB=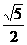 ,则cosA等于
,则cosA等于
A.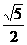 B.
B.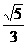 C.
C.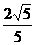 D.
D.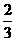
答案:B
提示:∵tanB=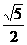 ,
,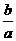 =
=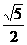 ,可令b=
,可令b=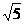 ,a=2,则c=3,cosA=
,a=2,则c=3,cosA=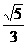 .
.
9.在Rt△ABC中, 2sin(α+20°)=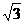 ,则锐角α的度数是
,则锐角α的度数是
A.60° B.80° C.40° D.以上结论都不对
答案:C
提示:2sin(α+20°)=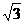 ,得sin(α+20°)=
,得sin(α+20°)=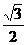 ,
,
所以α+20°=60°,α=40°.
8.在Rt△ABC中,各边都扩大四倍,则锐角A的各三角函数值
A.没有变化 B.分别扩大4倍
C.分别缩小到原来的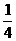 D.不能确定
D.不能确定
答案:A
提示:因为各边都扩大四倍,它们的比值不变,故三角函数值也不变.
7.在△ABC中,∠C=90°,下列式子正确的是
A.b=atanA B.b=csinA C.a=ccosB D.c=asinA
答案:C
提示:因为cosB=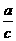 ,所以a=ccosB.
,所以a=ccosB.
6.如图9-43,AB、CD是两栋楼,且AB=CD=30 m,两楼间距AC=24 m,当太阳光与水平线的夹角为30°时,AB楼在CD楼上的影子是m.(精确到0.1 m)
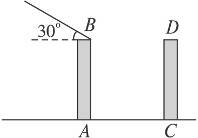
图9-43
答案:16.2
提示:画出图形,解直角三角形.
5.若∠A为锐角,且tan2A+2tanA-3=0,则∠A=__________________.
答案:45°
提示:解这个一元二次方程,可得tanA的值,但∠A为锐角,所以只能取正值.
4.等腰三角形的两条边长分别是4 cm,9 cm,则等腰三角形的底角的余弦值是________________.
答案: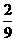
提示:三角形三边只能为4,9,9.
3.6tan230°-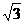 sin60°-2cos45°=__________________.
sin60°-2cos45°=__________________.
答案: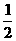 -
-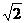
提示:tan30°=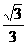 ,sin60°=
,sin60°=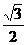 ,cos45°=
,cos45°=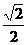 .
.
2.在△ABC中,若︱sinA-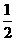 ︱+(
︱+(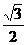 -cosB)2=0, 则∠C=___________________.
-cosB)2=0, 则∠C=___________________.
答案:120°
提示:由sinA=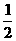 ,可得∠A=30°,
,可得∠A=30°,
由cosB=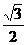 ,得∠B=30°,则∠C=120°.
,得∠B=30°,则∠C=120°.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com