
题目列表(包括答案和解析)
7.某校九年级一、二班学生参加同一次数学测验,经统计计算后得到下表:
|
班级 |
参加人数 |
中位数 |
方差 |
平均数 |
|
一班 |
55 |
78 |
135 |
75 |
|
二班 |
55 |
81 |
126 |
75 |
小亮根据上表分析得出如下结论:①一、二两班学生的平均水平相同;②二班的优秀人数多于一班的优秀人数(成绩≥80分为优秀);③一班成绩波动情况比二班成绩波动大.上述结论正确的是
A.①②③ B.①② C.①③ D.②③
答案:A
提示:平均数刻画数据的平均水平,中位数也可以说明中等水平来比较优秀人数,方差来刻画成绩的波动,从图表中相关数据来看,三个结论都对.
6.一组数据的方差为9,将这组数据中的每个数据扩大3倍,得到一组新数据的方差是
A.9 B.27 C.81 D.243
答案:C
提示:每个数据扩大3倍,则方差扩大为原来的9倍,所以9×9=81,选C.
5.为了解一批牛奶的重量,从中抽取10袋牛奶分别称出重量,此问题中,10袋牛奶的重量是
A.个体 B.总体 C.样本 D.都不对
答案:C
提示:总体、样本的定义,10袋牛奶的重量是从总体中抽出来的样本.
4.从100袋同一种糖果中随机抽出10袋称重,重量分别如下(单位:g):500,495,501,499,492,505, 500,497,501,500,请你估计这100袋糖果的总重量约为_________________g.
答案:49 900
提示:先求出每袋的平均质量,再乘以100,即用样本质量来估计总体的质量.
3.若数据1,2,3,2的平均数为a,中位数为b,众数为c,则数据a、b、c的方差是_____________.
答案:0
提示:数据1,2,3,2的平均数为2,中位数为2,众数为2,再利用方差的求法.
2.已知一组数据x,9.8,10.2,10.3的平均数是10,则这组数据的标准差是___________________.
答案:0.25
提示:根据平均数先求出x的值,再求出方差,标准差为方差的算术平方根.
1.为了调查现在中学生的身体状况,从某地市抽取100名初三学生测量了他们的体重,其中样本是指_________________.
答案:抽取的100名初三学生的体重
提示:所有的考察对象的全体叫做总体,每一个考察对象叫做个体,从总体中抽出一部分个体叫做样本.
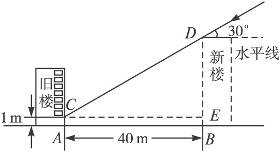
15.为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40 m,中午12时不能挡光.如图9-59,某旧楼的一楼窗台高1 m,要在此楼正南方40 m处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?(结果精确到1 m.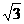 ≈1.732,
≈1.732,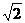 ≈1.414)
≈1.414)
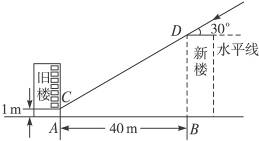
图9-59
解:过点C作CE⊥BD于E,∵AB=40 m,
∴CE=40 m.
∵阳光入射角为30°,
∴∠DCE=30°.
在Rt△DCE中,tan∠DCE=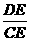 ,
,
∴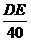 =
=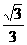 .
.
∴DE=40×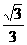 ≈23,而AC=BE=1 m,
≈23,而AC=BE=1 m,
∴DB=BE+ED=1+23=24(m).
答:新建楼房最高约24 m.
提示:将BD的长度转化成DE与BE的和,在△CED中,利用三角函数求出DE的长度,从而求解.
14.如图9-58,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
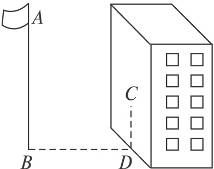
图9-58
答案:根据题意,设旗杆的高度是x米,则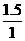 =
=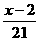 ,得x=33.5.
,得x=33.5.
提示:关键是同一时刻物高与影长成正比.2米的影长与产生该影长的物高的长度是一致的.
13.如图9-57,已知AB和DE是直立在地面上的两根立柱.AB=5 m,某一时刻AB在太阳光下的投影BC=3 m.
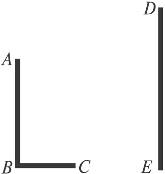
图9-57
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6 m,计算DE的长.
(1)答案:连结AC,过D作AC的平行线DF与地面交于F,则EF就是DE在阳光下的投影.
提示:太阳光线是平行的.
(2)答案:根据题意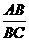 =
=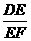 ,即
,即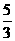 =
=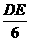 ,得DE=10.
,得DE=10.
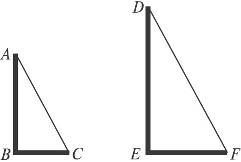
提示:同一时刻物高与影长成正比.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com