
题目列表(包括答案和解析)
23.(本题10分) 、
、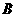 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往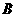 城,乙车驶往
城,乙车驶往 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距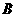 城高速公路入口处的距离
城高速公路入口处的距离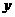 (千米)与行驶时间
(千米)与行驶时间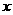 (时)之间的关系如图.
(时)之间的关系如图.
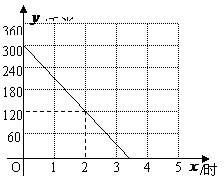 (1)求
(1)求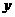 关于
关于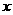 的表达式;
的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为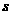 (千米).请直接写出
(千米).请直接写出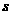 关于
关于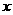 的表达式;
的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为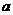 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度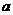 .在下图中画出乙车离开
.在下图中画出乙车离开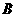 城高速公路入口处的距离
城高速公路入口处的距离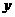 (千米)与行驶时间
(千米)与行驶时间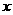 (时)之间的函数图象.
(时)之间的函数图象.
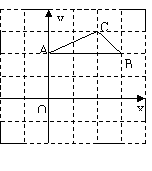
22.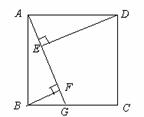 (本题10分)如图①,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(本题10分)如图①,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1) 求证:DE-BF = EF.
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系,
并说明理由.
(3) 若点G为CB延长线上一点,其余条件不变.
请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明).
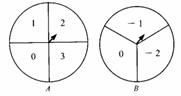
21、(本题满分8分)有两个可以自由转动的均匀转盘A、B,分别
被分成4等份、3等份,并在每份内均标有数字,如图所示.
王扬和刘菲同学用这两个转盘做游戏,游戏规则如下:
①分别转动转盘A与B;②两个转盘停止后,将两个指针所指
份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止).
③如果和为0,王扬获胜;否则刘非获胜。(1)用列表法(或树状图)求王扬获胜的概率;
(2)你认为这个游戏对双方公平吗?请说明理由.
20.(本题8分)如图,在平面直角坐标系中,点A,B,C的坐标分别
为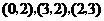 .
.
(1)请在图中画出 向下平移3个单位的像
向下平移3个单位的像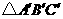 ;
;
(2)若一个二次函数的图象经过(1)中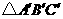 的三个顶点,
的三个顶点,
求此二次函数的关系式.
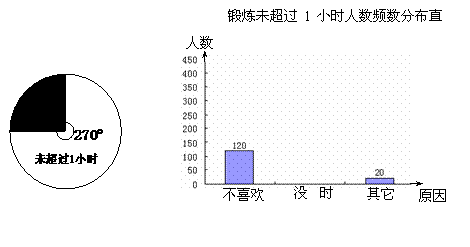
19.(本题6分)国家教委规定“中小学生每天在校体育活动时间不低于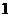 小时”.为此,.某中学为了了解学生体育活动情况,随机调查了
小时”.为此,.某中学为了了解学生体育活动情况,随机调查了 名毕业班学生,调查内容是:“每天锻炼是否超过
名毕业班学生,调查内容是:“每天锻炼是否超过 小时及未超过
小时及未超过 小时的原因”,所得的数据制成了的扇形统计图和频数分布直方图.根据图示,解答下列问题:
小时的原因”,所得的数据制成了的扇形统计图和频数分布直方图.根据图示,解答下列问题:
(1)若在被调查的学生中随机选出一名学生测试其体育成绩,选出的恰好是“每天锻炼超过 小时”的学生的概率是多少?
小时”的学生的概率是多少?
(2)“没时间”的人数是多少?并补全频数分布直方图;
 (3)
(3) 年这个地区初中毕业生约为3.2万人,按此调查,可以估计
年这个地区初中毕业生约为3.2万人,按此调查,可以估计 年这个地区初中毕业生中每天锻炼未超过
年这个地区初中毕业生中每天锻炼未超过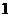 小时的学生约有多少万人?
小时的学生约有多少万人?
18.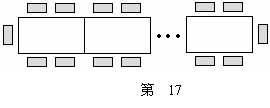 (本题6分)一种长方形餐桌的四周可以坐
(本题6分)一种长方形餐桌的四周可以坐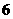 人用餐
人用餐
(带阴影的小长方形表示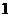 个人的位置).
个人的位置).
现把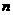 张这样的餐桌按如图方式拼接起来.
张这样的餐桌按如图方式拼接起来.
(1)问四周可以坐多少人用餐?(用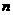 的代数式表示)
的代数式表示)
(2)若有 人用餐,至少需要多少张这样的餐桌
人用餐,至少需要多少张这样的餐桌
解答应写出文字说明、证明过程或推理步骤.如果觉得有些题有点困难,那么把自己
能写出的解答写出一部分也可以.
17.(本小题6分)
先化简,再求值: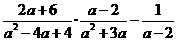 ,其中
,其中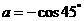 .
.
16. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.
点A1,A2,A3,…和点C1,C2,C3,…分别在直线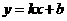 (k>0)
(k>0)
和x轴上,已知点B1(1,1),B2(3,2),
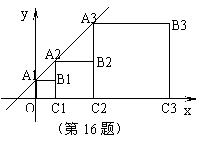 则Bn的坐标是_____▲ _________.
则Bn的坐标是_____▲ _________.
15.对于每个非零自然数n,抛物线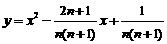 与x轴交于An、Bn两点,
与x轴交于An、Bn两点,
以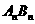 表示这两点间的距离,则
表示这两点间的距离,则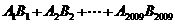 的值是 ▲
的值是 ▲
14.如图,已知圆锥的高为4,底面圆的直径为6,则此圆锥的侧面积是 ▲
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com