
题目列表(包括答案和解析)
14.(2010年山东新泰)在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0) 、C(12,16),由三个观测点确定的圆形区域是海洋生物保护区,如图所示.
、C(12,16),由三个观测点确定的圆形区域是海洋生物保护区,如图所示.
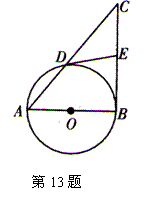
(1)求圆形区域的面积(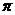 取3.14);
取3.14);
 (2)某时刻海面上出现一渔船A,在观测点O测得A位于北偏东45°方向上,同时在观测点B测得A位于北偏东30°方向上,求观测点B到渔船A的距离(结果保留三个有效
(2)某时刻海面上出现一渔船A,在观测点O测得A位于北偏东45°方向上,同时在观测点B测得A位于北偏东30°方向上,求观测点B到渔船A的距离(结果保留三个有效 数字);
数字);
(3)当渔船A由(2)中的位置向正西方向航行时,是否会进入海洋生物保护区?请通过计算解释.
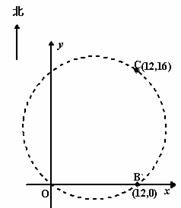
13.(2010年广西桂林适应训练)、以RtΔABC的直角边AB为直径作圆O,与斜边交于点D,E为BC边上的中点,连接DE.
 (1)求证:DE是⊙O的切线;
(1)求证:DE是⊙O的切线;
(2)连接OE、AE,当∠CAB为何值时,四边形AOED是平行四边形?并在此条件下求
sin∠CAE的值.
答案:(1)连接OD、BD
∵ΔBDC是RtΔ, 且E为BC中点。
∴∠EDB=∠EBD.
又∵OD=OB 且∠EBD+∠DBO=90°
∴∠EDB+∠ODB=90°
∴DE是⊙O的切线;
(2)∵∠EDO=∠B=90°,
若要AOED是平行四边形,则DE∥AB,D为AC中点。
又∵BD⊥AC,
∴ΔABC为等腰直角三角形。
∴∠CAB=45°.
过E作EH⊥AC于H.
设BC=2k,
则EH=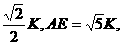
∴sin∠CAE=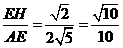
12.(2010年聊城冠县实验中学二模) 如下图所示,以Rt△ABC的直角边AB为直径作圆O,与斜边交于点D,E为BC边上的中点,连接DE。
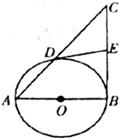
(1)求证:DE是⊙O的切线;
(2)连接OE,AE,当∠CAB为何值时,四边形AOED是平行四边形?
解(1)连接OD与BD.
∵△BDC是Rt△,且E为BC中点
∴∠EDB=∠EBD
又∵OD=OB且∠EBD+∠DBO=90°
∴∠EDB+∠ODB=90°
∴DE是⊙O的切线
(2)∵∠EDO=∠B=90°,若要AOED是平行四边形,则DE∥AB,D为AC中点
又∵BD⊥AC
∴△ABC为等腰直角三角形
∴∠CAB=45°
11. (2010年北京市朝阳区模拟)如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
(2010年北京市朝阳区模拟)如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.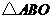 的三个顶点
的三个顶点 、
、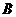 、
、 都在格点上.
都在格点上.
(1)画出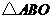 绕点
绕点 逆时针旋转
逆时针旋转 后得到的三角形;
后得到的三角形;
(2)求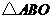 在上述旋转过程中所扫过的面积.
在上述旋转过程中所扫过的面积.

解:(1)画图正确(如图).
(2) 所扫过的面积是:
所扫过的面积是:
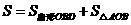
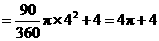 .
.
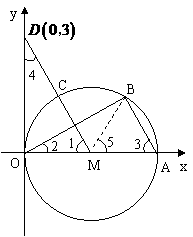
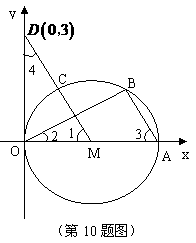
10.(2010年 湖里区 二次适应性考试)已知:如图,
直径为 的
的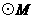 与
与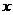 轴交于点O、A,
轴交于点O、A, 点
点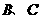 把弧
把弧
OA分为三等分,连结 并延长交
并延长交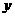 轴
轴 于D(0
于D(0 ,3).
,3).
(1)求证: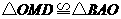 ;
;
(2)若直线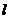 :
: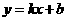 把
把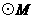 的
的
面积分为二等分,求证: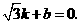
答案:证明:
(1)连接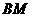 ,∵OA是直径,且
,∵OA是直径,且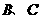 把弧OA三等分,∴
把弧OA三等分,∴ ,
,
又∵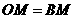 ,∴
,∴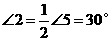 ,
,
又∵OA为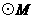 直径,∴
直径,∴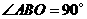 ,∴
,∴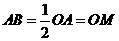 ,
,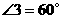 ,
,
∴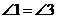 ,
,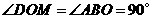 ,
,
在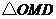 和
和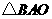 中,
中,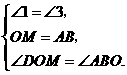
∴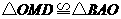 (ASA)
(ASA)
 (2)若直线
(2)若直线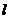 把
把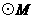 的面积分为二等份,
的面积分为二等份,
则直线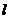 必过圆心
必过圆心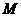 ,
,
∵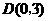 ,
,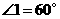 ,
,
∴在Rt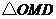 中,
中,
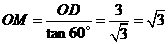 ,
,
∴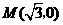 ,
,
把 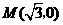 代入
代入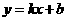 得:
得:
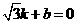 .
.
9.(2010年 湖里区 二次适应性考试)如图,四边形ABCD内接于⊙O,BD是⊙O的直径,
AE⊥CD于点E,DA平分∠BDE。
(1)求证:AE是⊙O的切线。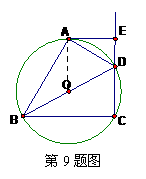 (2)若∠DBC=30°,DE=1 cm,求BD的长。
(2)若∠DBC=30°,DE=1 cm,求BD的长。
答案:
(1)证明:连结OA
∵AD平分∠BDE
∴∠ADE=∠ADO
∵OA=OD
∴∠OAD=∠ADO
∴∠ADE=∠OAD
∴OA∥CE
∵AE⊥CD
∴AE⊥OA
∴AE是⊙O的切线
(2)∵BD是⊙O的直径
∴∠BCD=90°
∵∠DBC=30°
∴∠BDE=120°
∵AD平分∠BDE
∴∠AD E=∠ADO=60°
E=∠ADO=60°
∵OA=OD
∴△OAD是等边三角形
∴AD=OD=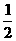 BD
BD
在Rt△AED中,DE=1,∠ADE=60°
∴AD=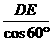 = 2
= 2
 ∴BD=4
∴BD=4
8.(2010年 湖里区 二次适应性考试)如图,线段AB与⊙O相切于点C,连结OA,OB,
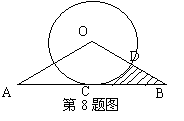 OB交⊙O于点D,已知
OB交⊙O于点D,已知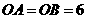 ,
,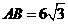 .
.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
答案:(1)连结OC,∵AB与⊙O相切于点C
∴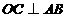 .
.
∵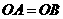 ,∴
,∴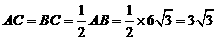 .
.
在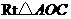 中,
中,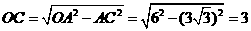 .
.
∴ ⊙O的半径为3.
(2)在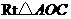 中∵ OC=
中∵ OC=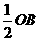 ,
∴ ∠B=30o, ∠COD=60o.
,
∴ ∠B=30o, ∠COD=60o.
∴扇形OCD的面积为
 =
=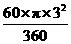 =
=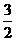 π.
π.
阴影部分的面积为
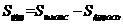
=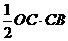 -
-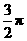 =
=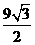 -
-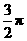 .
.
7.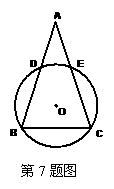 (2010年 湖里区 二次适应性考试)已知:如图,△ABC的中,AB=AC,点B、C都在⊙O上,AB、AC交⊙O于D、E两点,求证:
(2010年 湖里区 二次适应性考试)已知:如图,△ABC的中,AB=AC,点B、C都在⊙O上,AB、AC交⊙O于D、E两点,求证: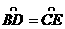
答案:证明:∵AB=AC
∴∠B=∠C
∴
∵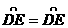
∴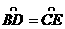
6.(2010年长沙市中考模拟)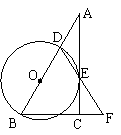 在
在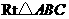 中,
中,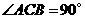 ,
, 是
是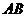 边上一点,以
边上一点,以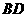 为直径的
为直径的 与边
与边 相切于点
相切于点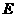 ,连结
,连结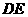 并延长,与
并延长,与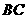 的延长线交于点
的延长线交于点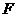 .
.
(1)求证: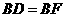 ;
;
(2)若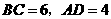 ,求
,求 的面积.
的面积.
答案:1)证明:连结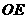 。
。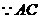 切
切 于
于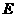 ,
,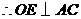 ,
,
又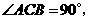 即
即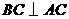 ,
,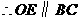 ,
,
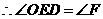 。又
。又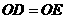 ,
,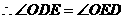 ,
,
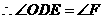 ,
, 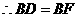 。
。
(2)设 半径为
半径为 ,由
,由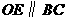 得
得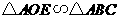 .
.
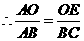 ,即
,即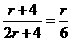 ,
,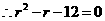 ,
,
解之得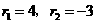 (舍)。
(舍)。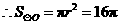 。
。
5. (2010年
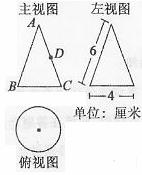
中考模拟2)如图是一个几何体的三视图 .
(2010年
中考模拟2)如图是一个几何体的三视图 .
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程 .
答案:
圆锥;
 表面积
表面积
S=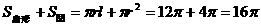 (平方厘米)
(平方厘米)
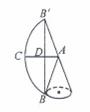
如图将圆锥侧面展开,线段BD为所求的最短路程 .
由条件得,∠BAB′=120°,C为弧BB′中点,所以BD=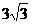 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com