
题目列表(包括答案和解析)
3.如图7-16,如果AB∥EF,BC∥DE,那么∠E和∠B满足___________________的关系.
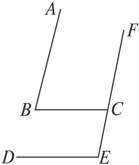
图7-16
答案:互补
提示:平行线的性质.
2.命题“平行于同一条直线的两直线平行”的条件是_____________,结论是______________,该命题是_______________命题(填“真”或“假”).
答案:两条直线平行于同一条直线 这两条直线平行 真
提示:命题的定义.
1.小明用图7-15的方法作了两条平行线,他的根据是____________________.
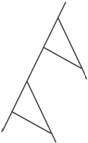
图7-15
答案:同位角相等,两直线平行
提示:平行线的判定.
20.(2010年广州中考数学模拟试题一)如图①②,图①是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为5个单位(每个单位为5cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=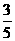 .
.
(1)求点M离地面AC的高度BM(单位:厘米);
(2)设人站立点C与点A的水平距离AC 等于11个单位,求铁环钩MF的长度(单位:厘米).

答案:过M作AC平行的直线,与OA,FC分别相交于H,N.
(1)在Rt△OHM中,∠OHM=90°,OM=5,HM=OM×sinα=3,所以OH=4,MB=HA=5-4=1(单位),1×5=5(cm),所以铁环钩离地面的高度为5cm.
(2)因为∠MOH+∠OMH= ∠OMH+∠FMN=90°,∠FMN=∠MOH=α,所以
∠OMH+∠FMN=90°,∠FMN=∠MOH=α,所以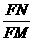 =sinα=
=sinα=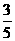 ,即得FN=
,即得FN=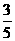 FM,在Rt△FMN中,∠FNM=90°,MN=BC=AC-AB=11-3=8(单位),由勾股定理FM2=FN2+MN2,即FM2=(
FM,在Rt△FMN中,∠FNM=90°,MN=BC=AC-AB=11-3=8(单位),由勾股定理FM2=FN2+MN2,即FM2=(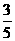 FM)2+82,解得FM=10(单位),10×5=50(cm),所以铁环钩的长度FM为50cm.
FM)2+82,解得FM=10(单位),10×5=50(cm),所以铁环钩的长度FM为50cm.
19.(2010年天水模拟)如图,AB是⊙O是直径,过A作⊙O的切线,在切线上截取AC=AB,连结OC交⊙O于D,连结BD并延长交AC于E,⊙F是△ADE的外接圆,⊙F在AE上.
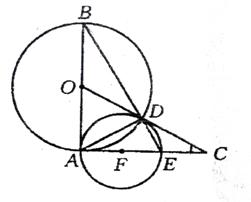 求证:(1)CD是⊙F的切线;
求证:(1)CD是⊙F的切线;
(2)CD=AE.
证明:(1)连接DF
∵CA 切⊙O于A,∴∠CAB=90°
又∵∠OAD=∠ODA ∠FAD=∠FDA
∴∠OAC=∠ODF=90°
∴∠FDC=90
∴CD是⊙F的切线
(2)FDC=DAC=90
∠C=∠C
∴△CDF∽△CAO
又∵AC=AB
∴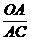 =
=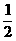 =
=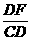
又∵DF=FE AE=2DF
∴AE=CD
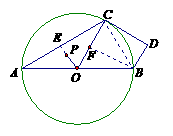
18.(2010年厦门湖里模拟)如图,已知AB是⊙O的直径,点C在⊙O上,P是△OAC的重心,且OP=,∠A=30º.
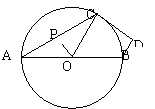 (1)求劣弧的长;
(1)求劣弧的长;
(2)若∠ABD=120º,BD=1,求证:CD是⊙O的切线.
答案:.(1)解:延长OP交AC于E,
∵ P是△OAC的重心,OP=,
∴ OE=1,
且 E是AC的中点.
 ∵ OA=OC,∴ OE⊥AC.
∵ OA=OC,∴ OE⊥AC.
在Rt△OAE中,∵ ∠A=30°,OE=1,
∴ OA=2.
∴ ∠AOE=60°.
∴ ∠AOC=120°.
∴ ︵AC=π.
(2)证明:连结BC.
∵ E、O分别是线段AC、AB的中点,
∴ BC∥OE,且BC=2OE=2=OB=OC.
∴ △OBC是等边三角形.
法1:∴ ∠OBC=60°.
∵ ∠OBD=120°,∴ ∠CBD=60°=∠AOE.
∵ BD=1=OE,BC=OA,
∴ △OAE ≌△BCD.
∴ ∠BCD=30°.
∵ ∠OCB=60°,
∴ ∠OCD=90°.
∴ CD是⊙O的切线.
法2:过B作BF∥DC交CO于F.
∵ ∠BOC=60°,∠ABD=120°,
∴ OC∥BD.
∴ 四边形BDCF是平行四边形.
∴ CF=BD=1.
∵ OC=2,
∴ F是OC的中点.
∴ BF⊥OC.
∴ CD⊥OC.
∴ CD是⊙O的切线.
17.(2010年厦门湖里模拟) 如图,已知在⊙O中,AB=4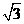 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
(1)求图中阴影部分的面积;
 (2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
答案:(1)∵∠A=30° AC⊥BD
∴BF=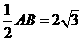 ∠BOC=∠COD=60° OB=2OF
∠BOC=∠COD=60° OB=2OF
∴OF=2,OB=4
S阴=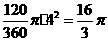
(2)根据题意得: 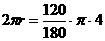 ∴
∴ =
=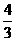
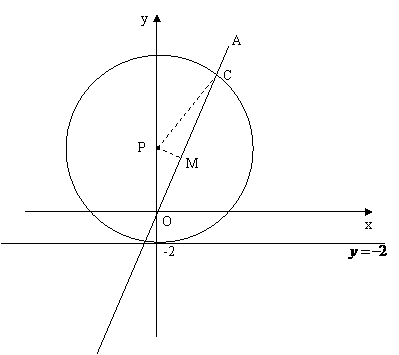
16.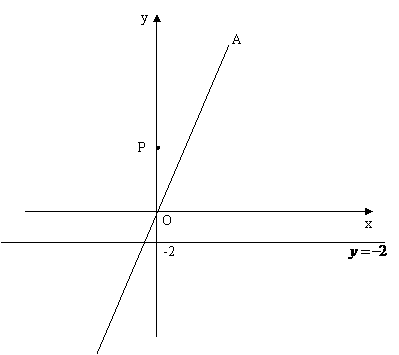 (2010年江西南昌一模)如图,在平面直角坐标系中,
(2010年江西南昌一模)如图,在平面直角坐标系中,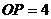 ,直线OA与
,直线OA与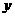 轴的夹角为
轴的夹角为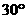 ,以P为圆心,
,以P为圆心, 为半径作⊙P,与
为半径作⊙P,与 交于点
交于点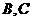 .
.
当r为何值时,△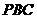 为等边三角形?
为等边三角形?
当⊙P与直线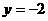 相切时,求
相切时,求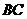 的值.
的值.
答案:(1)作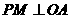 于M.
于M.
∵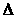
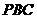 是等边三角形,
是等边三角形,
∴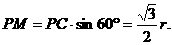
∵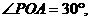
∴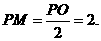
 ∴
∴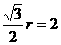
∴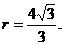
(2)连结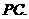
∵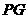 与直线
与直线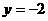 相切,
相切,
∴⊙P的半径为4+2=6.
∴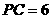
则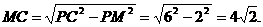
∵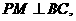
∴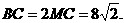
15.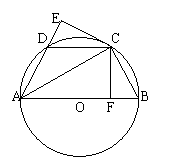 (2010年浙江杭州)已知:如图,AB是⊙O的直径,点C、D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
(2010年浙江杭州)已知:如图,AB是⊙O的直径,点C、D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积.
(1)∵ 弧CB=弧CD
∴ CB=CD,∠CAE=∠CAB
又∵ CF⊥AB,CE⊥AD
∴ CE=CF
∴ △CED≌△CFB
∴ DE=BF
(2)易得:△CAE≌△CAF
易求: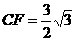
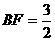
∴ 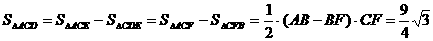
16.(1)314;(2)4;
(3)28.4>18,所以渔船A不会进入海洋生物保护区.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com