
题目列表(包括答案和解析)
9.(2010年江苏省泰州市济川实验初中中考模拟题) 如图1,把一个边长为2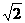 的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).
的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).
(1)求抛物线c1的解析式及点M、N的坐标;
(2)如图2,另一个边长为2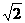 的正方形
的正方形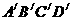 的中心G在点M上,
的中心G在点M上,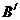 、
、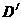 在x轴的负半轴上(
在x轴的负半轴上(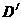 在
在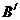 的左边),点
的左边),点 在第三象限,当点G沿着抛物线c1从点M移到点N,正方形随之移动,移动中
在第三象限,当点G沿着抛物线c1从点M移到点N,正方形随之移动,移动中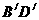 始终与x轴平行.
始终与x轴平行.
①直接写出点 、
、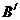 移动路线形成的抛物线
移动路线形成的抛物线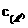 、
、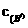 的函数关系式;
的函数关系式;
 ②如图3,当正方形
②如图3,当正方形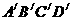 第一次移动到与正方形ABCD有一边在同一直线上时,
第一次移动到与正方形ABCD有一边在同一直线上时,

 求点G的坐标.
求点G的坐标.
答案:(1)y=-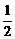 x2+4, M(
x2+4, M(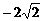 ,0),N(
,0),N(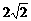 ,0)
,0)
①yA'=-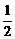 x2+2 ,
yB'=-
x2+2 ,
yB'=-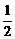 (x-2)2+4 ②G(1-
(x-2)2+4 ②G(1-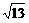 ,-3+
,-3+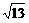
 )
)
8. (2010年江苏省泰州市济川实验初中中考模拟题)已知抛物线
(2010年江苏省泰州市济川实验初中中考模拟题)已知抛物线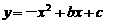 的部分图象如图所示.
的部分图象如图所示.
(1)求b、c的值;
(2)求y的最大值;
(3)写出当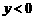 时,x的取值范围.
时,x的取值范围.
答案:(1)b=-2,c=3
(2) 4
(3) x<-3或x>1
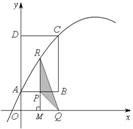
7.(2010年吉林中考模拟题)如图,在直角坐标系中,矩形ABCD的边AD在y轴正半轴上,点A、C的坐标分别为(0,1)、(2,4).点P从点A出发,沿A→B→C以每秒1个单位的速度运动,到点C停止;点Q在x轴上,横坐标为点P的横、纵坐标之和.抛物线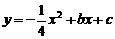 经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).
经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).
(1)求抛物线对应的函数关系式.
(2)分别求t=1和t=4时,点Q的坐标.
(3)当0<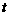 ≤5时,求S与t之间的函数关系式,并直接写出S的最大值.
≤5时,求S与t之间的函数关系式,并直接写出S的最大值.
[参考公式:抛物线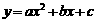 的顶点坐标为
的顶点坐标为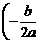 ,
,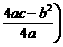 .]
.]
答案:(1)由抛物线经过点A(0,1),C(2,4),
得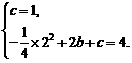 解得
解得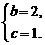
∴抛物线对应的函数关系式为: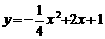 .
.
(2)当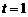 时,P点坐标为(1,1),∴Q点坐标为(2,0).
时,P点坐标为(1,1),∴Q点坐标为(2,0).
当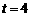 时,P点坐标为(2,3),∴Q点坐标为(5,0).
时,P点坐标为(2,3),∴Q点坐标为(5,0).
(3)当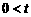 ≤2时,
≤2时,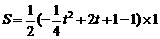 .
.
S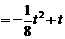 .
.
当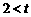 ≤5时,
≤5时,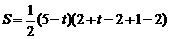 .
.
S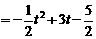 .
.
当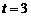 时,S的最大值为2.
时,S的最大值为2.
6.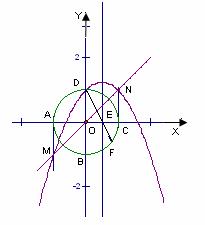 (2010年河南中考模拟题6)如图,在平面
(2010年河南中考模拟题6)如图,在平面 直角坐标系x0y中,半径为1的圆的圆心O在坐标原点,且与两坐标轴分别交于A、B、C、D四点。抛物线
直角坐标系x0y中,半径为1的圆的圆心O在坐标原点,且与两坐标轴分别交于A、B、C、D四点。抛物线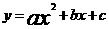 与y轴交于点D,与直线y=x交于点M、N,且MA、NC分别与圆O相切与点A和点C。
与y轴交于点D,与直线y=x交于点M、N,且MA、NC分别与圆O相切与点A和点C。
(1)求抛物线的解析式;
(2)抛物线的对称轴交x轴于点E,连接DE,并延长DE交圆O于F,求EF的长;
(3)过点B作圆O的切线交DC的延长线于点P,判断点P是否在抛物线上,说明理由。
答案:(1)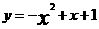 ,
,
(2)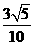 ,
,
(3)点P在抛物线上,
设yDC=kx+b,将(0,1),(1,0),带入得k=-1,b=1,
∴直线CD为y=-x+1,
∵过点B作⊙O的切线BP与x轴平行,
∴P点的纵坐标为-1,
把y=-1带入y=-x+1得x=2,
∴P(2,-1),
将x=2带入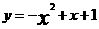 ,得 y=-1,
,得 y=-1,
∴点P在抛物线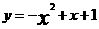 上。
上。
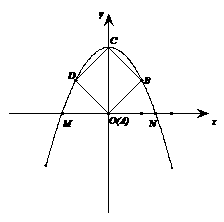
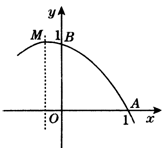
5.(2010年河南中考模拟题5)二次函数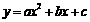 的图象的一部分如图所示.已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,l).
的图象的一部分如图所示.已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,l).
(1)试求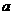 ,
,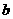 所满足的关系式;
所满足的关系式;
(2)设此二次函数的图象与x轴的另一个交点为C,当△AMC的面积为△ABC面积
的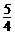 倍时,求a的值;
倍时,求a的值;
 (3)是否存在实数a,使得△ABC为直角三角形.若存在,请求出a的值;若不存在,请说明理由.
(3)是否存在实数a,使得△ABC为直角三角形.若存在,请求出a的值;若不存在,请说明理由.
答案:解 :(1)将A(1,0),B(0,l)代入
:(1)将A(1,0),B(0,l)代入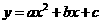 得
得
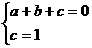 ,可得:
,可得: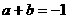
(2)由(1)可知: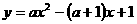 ,顶点M的纵坐标为
,顶点M的纵坐标为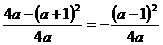 ,
,
因为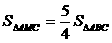 ,由同底可知:
,由同底可知: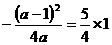 ,
,
整理得: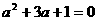 ,得:
,得: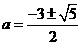
由图象可知: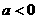 ,因为抛物线过点(0,1),顶点M在第二象限,其对称轴x=
,因为抛物线过点(0,1),顶点M在第二象限,其对称轴x=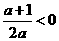 ,
,
∴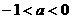 , ∴
, ∴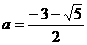 舍去,从而
舍去,从而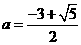
(3)① 由图可知,A为直角顶点不可能;
② 若C为直角顶点,此时与原点O重合,不合题意;
③ 若设B为直角顶点,则可知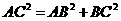 ,得:
,得:
令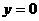 ,可得:
,可得: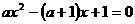 ,
,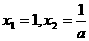
得: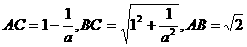
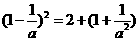 .
.
解得: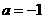 ,由-1<a<0,不合题意.所以不存在.
,由-1<a<0,不合题意.所以不存在.
综上所述: 不存在.
不存在.
4.(2010年河南中考模拟题4)如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
(1)点A的坐标是__________,点C的坐标是__________;
(2)设△OMN的面积为S,求S与t的函数关系式;
(3)探求(2)中得到的函数S有没有最大值?若有,求出最大值;若没有,说明理由.
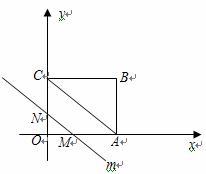
答案:(1)(4,0) (0,3)
(2)当0<t≤4时,OM=t.
由△OMN∽△OAC,得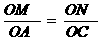 ,
,
∴ ON=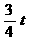 ,S=
,S=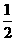 ×OM×ON=
×OM×ON=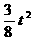 . (6分)
. (6分)
当4<t<8时,
如图,∵ OD=t,∴ AD= t-4.
由△DAM∽△AOC,可得AM=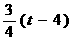 .(7分)
.(7分)
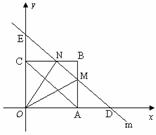 而△OND的高是3.
而△OND的高是3.
S=△OND的面积-△OMD的面积
=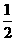 ×t×3-
×t×3-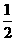 ×t×
×t×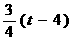
=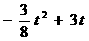 . ( 10分)
. ( 10分)
(3) 有最大值.
方法一:
当0<t≤4时,
∵ 抛物线S=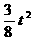 的开口向上,在对称轴t=0的右边, S随t的增大而增大,
的开口向上,在对称轴t=0的右边, S随t的增大而增大,
∴ 当t=4时,S可取到最大值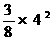 =6; (11分)
=6; (11分)
当4<t<8时,
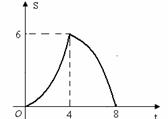 ∵ 抛物线S=
∵ 抛物线S=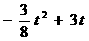 的开口向下,它的顶点是(4,6),
的开口向下,它的顶点是(4,6),
∴ S<6.
综上,当t=4时,S有最大值6.
方法二:
∵ S=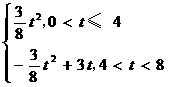
∴ 当0<t<8时,画出S与t的函数关系图像,如图所示.
显然,当t=4时,S有最大值6.
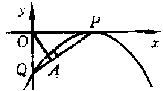
2.(2010年河南中考模拟题1)如图,已知,抛物线 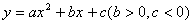
的顶点P在x轴上,与y轴交于点Q,过坐标原点O作 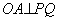 ,垂足为A,且
,垂足为A,且
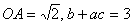
(1)求b的值;
(2)求抛物线的解析式。
答案:(1) 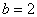
(2) 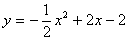
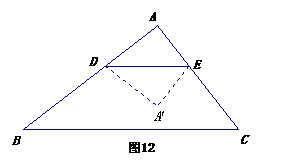 3.(2010年河南中考模拟题3)如图,在
3.(2010年河南中考模拟题3)如图,在 中,∠
中,∠
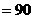 °,
°,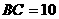 ,
, 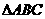 的面积为
的面积为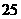 ,点
,点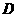 为
为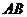 边上的任意一点(
边上的任意一点(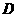 不与
不与 、
、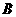 重合),过点
重合),过点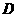 作
作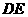 ∥
∥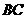 ,交
,交 于点
于点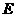 .设
.设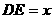 以
以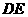 为折线将△
为折线将△ 翻折,所得的
翻折,所得的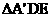 与梯形
与梯形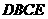 重叠部分的面积记为y.
重叠部分的面积记为y.
(1).用x表示∆ADE的面积;
(2).求出 ﹤
﹤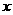 ≤
≤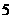 时y与x的函数关系式;
时y与x的函数关系式;
(3).求出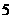 ﹤
﹤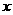 ﹤
﹤ 时y与x的函数关系式;
时y与x的函数关系式;
(4).当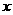 取何值时,
取何值时,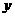 的值最大?最大值是多少?
的值最大?最大值是多少?
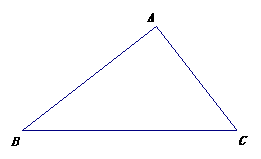
答案:(1)如图,设直线BC与⊙O相切于点D,连接OA、OD,则OA=OD=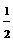 MN
MN
在Rt⊿ABC中,BC=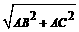 =5
=5
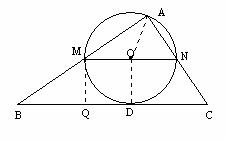 ∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C
∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C
⊿AMN∽⊿ABC,∴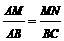 ,
,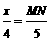 ,
,
∴MN=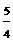 x, ∴OD=
x, ∴OD=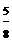 x
x
过点M作MQ⊥BC于Q,则MQ=OD=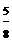 x,
x,
在Rt⊿BMQ和Rt⊿BCA中,∠B是公共角
∴Rt⊿BMQ∽Rt⊿BCA,
∴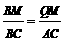 ,∴BM=
,∴BM=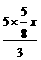 =
=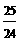 x,AB=BM+MA=
x,AB=BM+MA=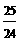 x +x=4,∴x=
x +x=4,∴x=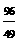
∴当x= 时,⊙O与直线BC相切,
时,⊙O与直线BC相切,
(3)随着点M的运动,当点P 落在BC上时,连接AP,则点O为AP的中点。
∵MN∥BC,∴∠AMN=∠B,∠AOM=∠APC
∴⊿AMO∽⊿ABP,∴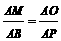 =
=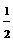 ,AM=BM=2
,AM=BM=2
故以下分两种情况讨论:
当0<x≤2时,y=S⊿PMN=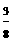 x2.
x2.
∴当x=2时,y最大=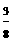 ×22=
×22=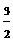
当2<x<4时,设PM、PN分别交BC于E、F
∵四边形AMPN是矩形,
∴PN∥AM,PN=AM=x
又∵MN∥BC,∴四边形MBFN是平行四边形
∴FN=BM=4-x,∴PF=x-(4-x)=2x-4,
又⊿PEF∽⊿ACB,∴(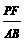 )2=
)2=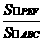
∴S⊿PEF=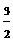 (x-2)2,y= S⊿PMN- S⊿PEF=
(x-2)2,y= S⊿PMN- S⊿PEF=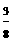 x-
x-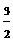 (x-2)2=-
(x-2)2=-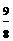 x2+6x-6
x2+6x-6
当2<x<4时,y=-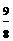 x2+6x-6=-
x2+6x-6=-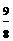 (x-
(x-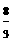 )2+2
)2+2
∴当x=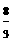 时,满足2<x<4,y最大=2。
时,满足2<x<4,y最大=2。
综合上述,当x=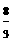 时,y值最大,y最大=2。
时,y值最大,y最大=2。
1.(2010年山东宁阳一模)某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不超过45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数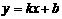 ,且
,且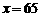 时,
时,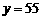 ;
;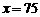 时,
时,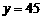 .
.
(1)若该商场获利为w元,试写出利润w与销售单价x之间的关系式,售价定为多少元时,商场可以获利最大,最大利润为多少元?
(2)若该商场获利不低于500元,试确定销售单价x的范围.
答案:(1)将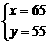
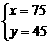 代入
代入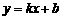 中
中
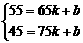
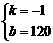 ∴
∴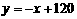
∴W =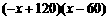
W =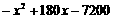
W =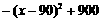
又∵60≤x≤60×(1+45%) 即60≤x≤87 则x=87时获利最多
将x=87代入,得W=-(87-90)2+900=891元
(2)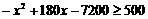
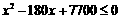
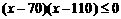
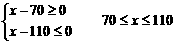
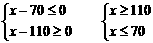 (舍去)
(舍去)
则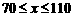 ,但
,但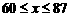 ∴
∴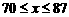
答:(1)x为87元有最大利润为891元;(2)范围为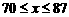
16.(2010年 湖里区
二次适应性考试)抛物线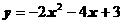 的顶点坐标是 .
的顶点坐标是 .
答案:(-1,5)
15.(2010重庆市綦江中学模拟1)抛物线y=(x-1)2+3的顶点坐标为 .
答案 (1,3) ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com