
题目列表(包括答案和解析)
7. 在九张大小质地都相同的卡片上分别写有数字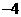 、
、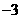 、
、 、
、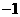 、
、 、
、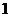 、
、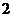 、
、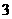 、
、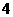 ,任意抽取一张卡片,则所抽卡片上数字的绝对值小于2的概率是
,任意抽取一张卡片,则所抽卡片上数字的绝对值小于2的概率是
A.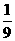 B.
B.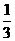 C.
C.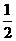 D.
D.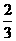
6. 已知关于x 的一元二次方程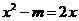 有两个不相等的实数根,则m的取值范围是
有两个不相等的实数根,则m的取值范围是
A. m> -1
B. m<-2 C.m ≥-1
D.m<1
-1
B. m<-2 C.m ≥-1
D.m<1
5. 某射击队要从四名运动员中选拔一名参加比赛,选拔赛中,每名队员的平均成绩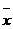
 与方差
与方差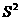 如下表所示.如
如下表所示.如
果要选择一个平均成绩高且发挥稳定的人参赛,那么这个人应是
|
|
甲 |
乙 |
丙 |
丁 |
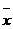 |
8 |
9 |
9 |
8 |
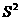 |
1 |
1 |
1.2 |
1.3 |

A.甲 B.乙 C.丙 D.丁
4.若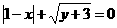 ,则
,则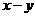 的值是
的值是
A.1 B.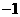 C.4 D.
C.4 D. 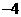
3.下列立体图形中,侧面展开图是扇形的是( )

2.2010年某市启动了历史上规模最大的轨道交通投资建设项目,预计某市轨道交通投资将达到51 800 000 000元人民币. 将51 800 000 000用科学记数法表示正确的是
 A.
5.18×1010 B.
51.8×109 C. 0.518×1011
D. 518×108
A.
5.18×1010 B.
51.8×109 C. 0.518×1011
D. 518×108
下列各题均有四个选项,其中只有一个是符合题意的.
1.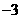 的倒数是
的倒数是
A.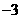 B.3 C.
B.3 C. 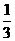 D.
D.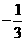
25.如图,在平面直角坐标系中,点A的坐标为(1,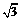 ) ,点B
) ,点B 在x轴的负半轴上,
在x轴的负半轴上,
∠ABO=30°.
(1)求过点A、O、B的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使AC+OC的值最小?若存在,求出点C的坐标;若不存在,请说明理由;
 (3)在(1)中
(3)在(1)中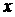 轴下方的抛物线上是否存在一点P,过点P作
轴下方的抛物线上是否存在一点P,过点P作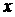 轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
24.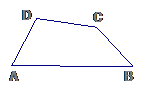 已知:如图,在四边形ABCD中,
AD=BC,∠A、∠B均为锐角.
已知:如图,在四边形ABCD中,
AD=BC,∠A、∠B均为锐角.
(1) 当∠A=∠B时,则CD与A B的位置关系是CD AB,大小关系是CD AB;
(2) 当∠A>∠B时,(1)中C D与A B的大小关系是否还成立,
证明你的结 论.
论.
23.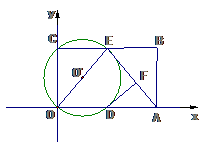 在平面直角坐标系
在平面直角坐标系 中,矩形
中,矩形 ABCO的面
ABCO的面 积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F.
积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F.
(1) 求OA,OC的长;
(2) 求证:DF为⊙O′的切线;
(3)由已知可得,△AOE是等腰三角形.那么在直线BC上是否存在除点E以外的点P,使△AOP也是等腰三角形?如果存在,请你证明点P与⊙O′的位置关系,如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com