
题目列表(包括答案和解析)
5.如图8-9,已知△ABC的六个元素,则图8-10中甲、乙、丙三个三角形中和△ABC全等的图形个数是
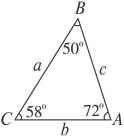
图8-9
A.1 B.2
C.3 D.0
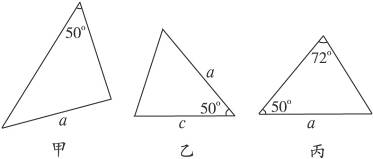
图8-10
答案:B
提示:乙和△ABC满足两角夹边,丙和△ABC满足两角和其中一角的对边,以上两个都可判定三角形全等.
4.△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后仍不一定能保证△ABC≌△DEF,则补充的这个条件为
A.BC=EF B.∠A=∠D
C.AC=DF D.∠C=∠F
答案:C
提示:补充AC=DF后,条件为两角对边对应相等,两个三角形不一定全等.
3.如图8-8,在△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的角平分线,则∠BOC=_______________.
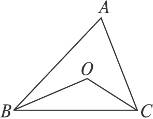
图8-8
答案:115°
提示:∠A=50°,依据三角形内角和定理,∠ABC+∠ACB=180°-50°=130°,BO、CO分别是∠ABC、∠ACB的角平分线,所以∠OBC+∠OCB= (∠ABC+∠ACB)=65°,∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°.
(∠ABC+∠ACB)=65°,∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°.
2.如图8-7,已知△ABC中,D是BC上一点,DE⊥AB,DF⊥AC,垂足分别为E、F.如果DE=DF,∠BAC=60°,AD=20 cm,那么DE的长是___________________ cm.
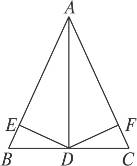
图8-7
答案:10
提示:DE⊥AB,DF⊥AC,可得∠AED=∠AFD=90°,又DE=DF,AD=AD,所以Rt△ADE≌Rt△ADF,∠EAD=30°,根据含有30°直角三角形的性质,DE= AD=10 cm.
AD=10 cm.
1.如图8-6,AD⊥AC,BC⊥BD,要想使△ADC≌△BCD,小王添加了一个条件AC=BD,其依据为______________,你还可以加一个条件______________,依据为______________.
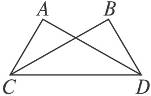
图8-6
答案:HL ∠ADC=∠BCD AAS
提示:由AC=BD以及公共边CD=DC,依据“HL”可判定两个直角三角形全等.∠ADC=∠BCD,∠A=∠B=90°,CD=DC,由“AAS”判定三角形全等.
16.如图9-48,在一次暖气管道的铺设工作中,工程是由A点出发沿正西方向进行的,在A点的南偏西60°的方向上有一所学校,学校占地是以B点为中心方圆100米的圆形,当工程进行了200米时到达C处,此时B在C的南偏西30°的方向上,请根据题中所提供的信息计算、分析一下,工程继续进行下去,是否会穿过学校?
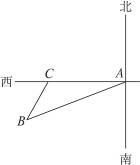
图9-48
解:过B作BD⊥AC于D,在Rt△BCD中,∠BCD=60°,
∵tan60°=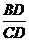 ,∴CD=
,∴CD=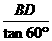 .
.
同理,在Rt△BAD中,AD=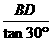 ,
,
又∵AD-CD=200,∴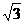 BD-
BD-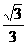 BD=200.
BD=200.
∴BD=100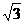 >100.∴不会穿过学校.
>100.∴不会穿过学校.
15.如图9-47,水面上有一浮标,在高于水面1米的地方观察,测得浮标顶的仰角30°,同时测得浮标在水中的倒影顶端俯角45°,观察时水面处于平静状态,求水面到浮标顶端的高度.(精确到0.1米)
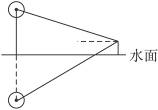
图9-47
答案:3.7米.
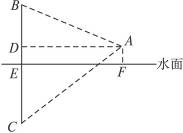
提示:过A作AD⊥BC于D,则∠BAD=30°,∠DAC=45°.
设BD=x,则AD=xcot30°.
又AD=DC且BE=DC,即x+1=xcot30°.
求得x≈2.73.
∴BE=2.73+1≈3.7(米).
14.如图9-46,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14米到达D,在D处测得A的仰角为45°,求铁塔AB的高.
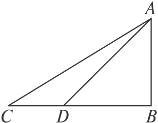
图9-46
解:在Rt△ABD中,
∵tan∠ADB=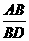 =1,∴BD=AB.
=1,∴BD=AB.
又在Rt△ABC中,∵tanC=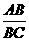 =
=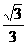 ,
,
∴BC=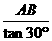 =
=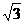 AB.
AB.
又∵BC-BD=14,∴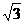 AB-AB=14.
AB-AB=14.
∴AB=7(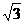 +1)(米).
+1)(米).
13.如图9-45,用测角仪测得铁塔顶点A的仰角为30°,测角仪离铁塔中心线AB 的距离为40米,测角仪CD高1.5米,求铁塔的高度.(精确到0.1米)
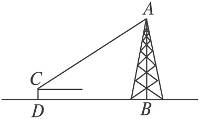
图9-45
答案:24.6米.
提示:铁塔的高度AB=40tan30°+1.5≈24.6(米).
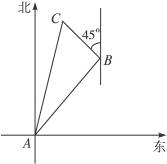
12.(2010四川泸洲中考)如图9-44,在一次实践活动中,小兵从A地出发,沿北偏东45°方向行进了5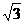 千米到达B地,然后再沿北偏西45°方向行进了5千米到达目的地点C.
千米到达B地,然后再沿北偏西45°方向行进了5千米到达目的地点C.
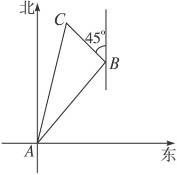
图9-44
(1)求A、C两地之间的距离;
(2)试确定目的地C在点A的什么方向?
解:根据题意,可知∠ABC=90°,
∵AB=5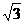 ,BC=5,
,BC=5,
AC2=AB2+BC2
=75+25
=100.
∴AC=10千米.
(2)在Rt△ABC中,tan∠BAC=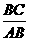 =
=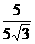 =
=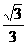 ,
,
∴∠BAC=30°.
∴C在点A的北偏东15°.
提示:根据方向角,先确定出△ABC是直角三角形,可用勾股定理求AC,再利用三角函数求出CA.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com