
题目列表(包括答案和解析)
4.点A(a,-3)与点B(-2,b)关于x轴对称,则a=_________________,b=__________________.
答案:-2 -3
提示:对称点的坐标.
3.已知点A(2a-8,2-a)是第三象限内的点,且横、纵坐标都是整数,则点P的坐标是___________.
答案:(-2,-1)
提示:象限点的坐标.
2.如果将“4排2号”简记作(4,2),那么“2排4号”表示为___________________.
答案:(2,4)
提示:坐标表示.
1.观察下列图象,如图7-25,与图(1)中的鱼相比,图(2)中的鱼发生了一些变化,若图(1)中鱼上点P的坐标为(4,3.2),则这个点在图(2)中的对应点P1的坐标应为___________________.
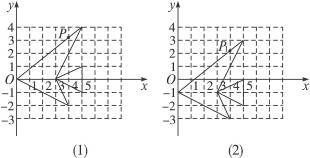
图7-25
答案:(4,2.2)
提示:平移.
11.如图8-16,线段BE上有一点C,以BC、CE为边分别在BE的同侧作等边三角形ABC、DCE,连结AE、BD,分别交CD、CA于Q、P.
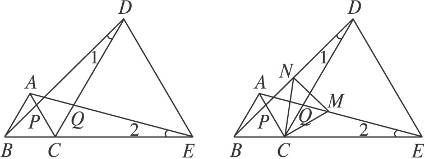
图8-16
(1)找出图中的一组相等的线段(等边三角形的边长相等除外),并说明你的理由.
(2)取AE的中点M、BD的中点N,连结MN,试判断△CMN的形状.
(1)答案:BD=AE.
证明:等边三角形ABC、DCE中,∠ACB=∠ACD=∠DCE=60°,∠BCD=∠ACE,BC=AC,DC=EC,所以△BCD≌△ACE(SAS).
(2)答案:等边三角形.
证明:由△BCD≌△ACE,可得∠1=∠2,BD=AE,M是AE的中点、N是BD的中点,所以DN=EM,又DC=CE,因此△DCN≌△ECM,∴CN=CM,∠NCD=∠MCE,∠MCE+∠DCM=60°,所以∠NCD+∠DCM=60°,即∠NCM=60°,△CMN为等边三角形.
10.如图8-15,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC中点.
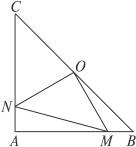
图8-15
(1)写出O点到△ABC三个顶点A、B、C的距离关系(不要求证明);
(2)如果M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,并证明你的结论.
(1)答案:OA=OB=OC.
提示:连结OA,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC中点,易证得△OAC≌△OAB,
又∠C=45°,所以∠OAC=45°,OC=OA,同理,OA=OB.
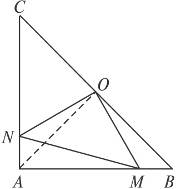
(2)答案:△OMN为等腰直角三角形.
证明:AN=BM,OA=OB,∠OAC=∠B=45°,△OAN≌△OBM,
得ON=OM,∠AON=∠BOM,又∠AOM+∠BOM=90°,
所以∠AON+∠AOM=90°,即∠MON=90°.
9.(2010辽宁大连中考)如图8-14,E、F分别是平行四边形ABCD对角线BD所在直线上两点,DE=BF,请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只需研究一组线段相等即可).
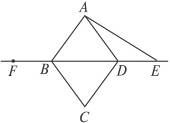
图8-14
(1)连结_______________;
(2)猜想:_______________;
(3)证明:
(说明:写出证明过程的重要依据)
如图.
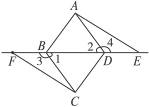
答案:(1)CF (2)CF=AE (3)∵四边形ABCD是平行四边形,∴AD BC,∴∠1=∠2(两直线平行,内错角相等).∵∠2+∠4=180°,∠1+∠3=180°,∴∠3=∠4.又∵DE=BF,
BC,∴∠1=∠2(两直线平行,内错角相等).∵∠2+∠4=180°,∠1+∠3=180°,∴∠3=∠4.又∵DE=BF,
∴△ADE≌△CBF(SAS).∴CF=AE.
提示:由平行四边形ABCD,可得对边相等,且∠FBC=∠ADE,又DE=BF,所以连结CF,即可创设全等三角形.
8.如图8-12,已知AE=CF,∠DAF=∠BCE,AD=CB.
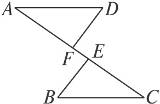
图8-12
(1)问:△ADF与△CBE全等吗?请说明理由.
(2)如果将△BEC沿CA边方向平行移动,可有图8-13中3幅图,如上面的条件不变,结论仍成立吗?请选择一幅图说明理由.
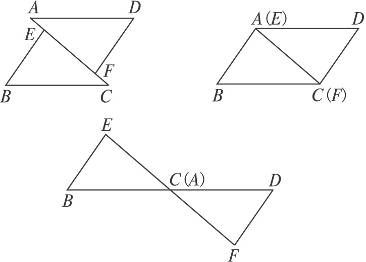
图8-13
答案:(1)全等.
提示:证明:∵AE=CF,∴AF=CE.
又∵∠DAF=∠BCE,AD=CB,∴△ADF≌△CBE.
答案:(2)成立.
提示:如第一幅图证明:
∵AE=CF,∴AF=CE.
又∵∠DAF=∠BCE,AD=CB,∴△ADF≌△CBE.
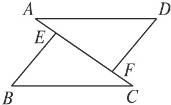
7.图8-11是将矩形纸片沿对角线折叠得到的,图中(包括实线、虚线在内)共有全等三角形_____________对.
图8-11
A.2 B.3
C.4 D.5
答案:D
提示:△ABD≌△EDB,△ABD≌△DCB,△EDB≌△DCB,△OBD和它下面重叠部分的三角形全等△AOB≌△DOE.
6.使两个直角三角形全等的条件是
A.两条边对应相等 B.一条边对应相等
C.两锐角对应相等 D.一锐角对应相等
答案:A
提示:两条边对应相等,有两种情况,其一两边若是两直角边,再加上夹角为直角,依据“SAS”判定全等;其二两边若是一直角边和斜边,可依据“HL”判定两直角三角形全等.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com