
题目列表(包括答案和解析)
14.(本小题满分5分)
解: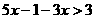 …………1分
…………1分
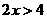 …………2分
…………2分
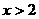 …………3分
…………3分
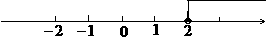
…………5分
13.(本小题满分5分)
解:原式﹦1+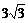 -
-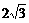 …………3分
…………3分
﹦1+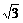 .
………5分
.
………5分
9.-1 10.55 11.(-1,2) 12.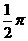
1B 2D 3A 4B 5D 6A 7D 8B
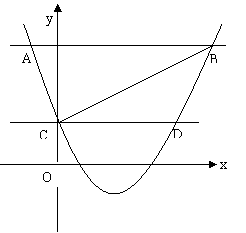
25.如图,抛物线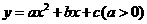 与
与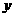 轴相交于点C,直线
轴相交于点C,直线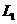 经过点C且平行于
经过点C且平行于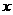 轴,将
轴,将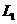 向上平移t个单位得到直线
向上平移t个单位得到直线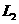 ,设
,设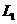 与抛物线的交点为C、D,
与抛物线的交点为C、D,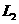 与抛物线的交点为A、B,连接 AC、BC.
与抛物线的交点为A、B,连接 AC、BC.
(1)当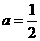 ,
,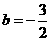 ,
,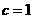 ,
,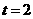 时,探究△ABC的形状,并说明理由;
时,探究△ABC的形状,并说明理由;
(2)若△AB C为直角三角形,求t的值(用含a的式子表示);
C为直角三角形,求t的值(用含a的式子表示);
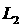 (3)在(2)的条件下,若点A关于
(3)在(2)的条件下,若点A关于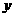 轴的对称点A’恰好在抛物线F的对称轴上,连接A’C,BD,求四边形A’CDB的面积(用含a的式子表示)
轴的对称点A’恰好在抛物线F的对称轴上,连接A’C,BD,求四边形A’CDB的面积(用含a的式子表示)
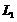
2011年密云县初中毕业考试数学试卷及评分标准
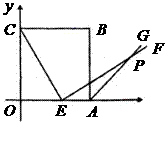
24.如图,边长为5的正方形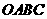 的顶点
的顶点 在坐标原点处,点
在坐标原点处,点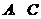 分别在
分别在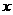 轴、
轴、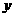 轴
轴
的正半轴上,点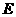 是
是 边上的点(不与点
边上的点(不与点 重合),
重合),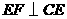 ,且与正方形外角平分
,且与正方形外角平分
线 交于点
交于点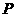 .
.
(1)当点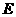 坐标为
坐标为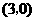 时,试证明
时,试证明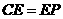 ;
;
(2)如果将上述条件“点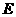 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点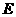 坐标为(
坐标为(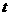 ,0)(
,0)(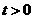 )”,结论
)”,结论
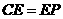 是否仍然成立,请
是否仍然成立,请 说明理由;
说明理由;
 (3)在
(3)在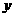 轴上是否存在点
轴上是否存在点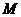 ,使得四边形
,使得四边形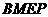 是平行四边形?若存在,请证明;若不存在,请说明理由.
是平行四边形?若存在,请证明;若不存在,请说明理由.
23.光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区,两地区与该农机租赁公司商定每天的租赁价格见下表:
|
|
每台甲型收割机的租金 |
每台甲型收割机的租金 |
|
A地区 |
1800 |
1600 |
|
B地区 |
1600 |
1200 |
(1)派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元)
求x与y间的函数关系时,并写出x的取值范围;
(2)若使农机租菱公司这50台联合收割机一天的租金总额比低于79600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提出一条合理建议。
22.类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+(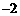 )=1.
)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移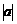 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移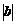 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为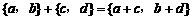 .
.
解决问题:
(1)计算:{3,1}+{1,-2};
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头
 Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
2121.刘明对本班同学的业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.
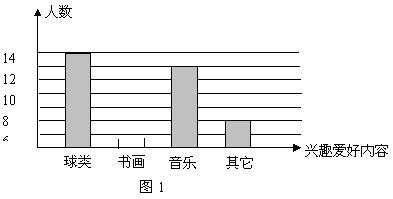
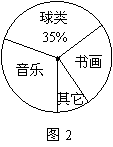
请你根据图中提供的信息,解答下列问题:
(1)在图1中,将“书画”部分 的图形补充完整;
的图形补充完整;
(2)在图2中,求出“球类”部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数.
20.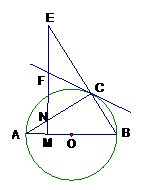 如图,AB是
如图,AB是 的直径,
的直径,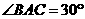 ,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且
,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且
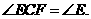
(1)证明CF是 的切线
的切线
(2) 设⊙O的半径为1.且AC=CE,求MO的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com