
题目列表(包括答案和解析)
7.函数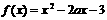 在区间[1,2]上存在反函数的充分必要条件是 ( )
在区间[1,2]上存在反函数的充分必要条件是 ( )
A.
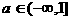 B.
B.
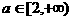
C.
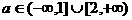 D.
D.
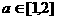
6.如图,在正方体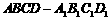 中,P是侧面
中,P是侧面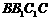 内一动点,若P到直线BC与
内一动点,若P到直线BC与
直线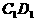 的距离相等,则动点P的轨迹所在的曲线是 ( )
的距离相等,则动点P的轨迹所在的曲线是 ( )
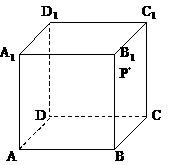
A. 直线 B. 圆 C. 双曲线 D. 抛物线
5.从长度分别为1,2,3,4的四条线段中,任取三条的不同取法共有n种,在这些取法中,
以取出的三条线段为边可组成的三角形的个数为m,则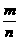 等于 ( )
等于 ( )
A.
0 B.
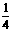 C.
C.
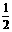 D.
D.
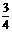
4.已知a、b、c满足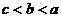 ,且
,且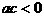 ,那么下列选项中一定成立的是 ( )
,那么下列选项中一定成立的是 ( )
A.
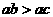 B.
B. 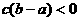 C.
C.
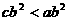 D.
D.
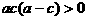
3.设m、n是两条不同的直线,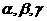 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若 ,
,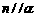 ,则
,则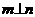 ②若
②若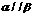 ,
,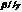 ,
, ,则
,则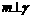
③若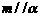 ,
,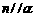 ,则
,则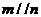 ④若
④若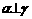 ,
,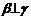 ,则
,则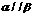
其中正确命题的序号是 ( )
A. ①和② B. ②和③ C. ③和④ D. ①和④
2.满足条件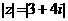 的复数
的复数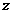 在复平面上对应点的轨迹是 ( )
在复平面上对应点的轨迹是 ( )
A. 一条直线 B. 两条直线 C. 圆 D. 椭圆
1.设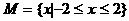 ,
,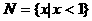 ,则
,则 等于 ( )
等于 ( )
A.
 B.
B.
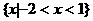 C.
C. 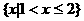 D.
D.
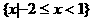
(17)(本题满分12分)
在ΔABC中,角A、B、C所对的边分别为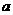 、b、c,且
、b、c,且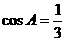 .
.
(Ⅰ)求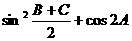 的值;
的值;
(Ⅱ)若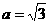 ,求bc的最大值.
,求bc的最大值.
(18)(本题满分12分)
盒子中有大小相同的球10个,其中标号为1的球3个,标号为2的球4个,标号为5的球3个,第一次从盒子中任取1个球,放回后第二次再任取1个球(假设取到每个球的可能性都相同).记第一次与第二次取到球的标号之和为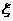 .
.
(Ⅰ)求随机变量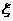 的分布列;
的分布列;
(Ⅱ)求随机变量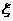 的期望
的期望 .
.
(19)(本题满分12分)
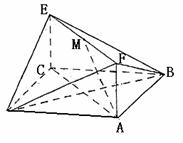 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, AB=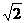 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求二面角A-DF-B的大小;
(Ⅲ)求点B到平面CMN的距离.
(20)(本题满分12分)
设曲线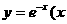 ≥0)在点M(t,e--t)处的切线
≥0)在点M(t,e--t)处的切线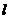 与x轴y轴所围成的三角形面积为S(t).
与x轴y轴所围成的三角形面积为S(t).
(Ⅰ)求切线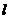 的方程;
的方程;
(Ⅱ)求S(t)的最大值.
(21)(本题满分12分)
已知双曲线的中心在原点,右顶点为A(1,0)点P、Q在双曲线的右支上,支M(m,0)到直线AP的距离为1.
(Ⅰ)若直线AP的斜率为k,且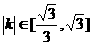 ,求实数m的取值范围;
,求实数m的取值范围;
(Ⅱ)当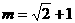 时,ΔAPQ的内心恰好是点M,求此双曲线的方程.
时,ΔAPQ的内心恰好是点M,求此双曲线的方程.
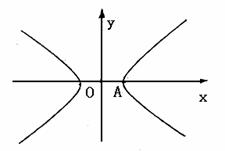
(22)(本题满分14分)
如图,ΔOBC的在个顶点坐标分别为(0,0)、(1,0)、(0,2),设P为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n,Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn),
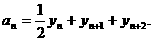
(Ⅰ)求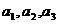 及
及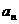 ;
;
(Ⅱ)证明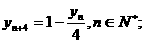
(Ⅲ)若记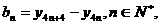 证明
证明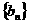 是等比数列.
是等比数列.
2004年普通高等学校招生全国统一考试
(13)已知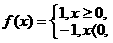 则不等式
则不等式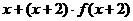 ≤5的解集是
.
≤5的解集是
.


 (14)已知平面上三点A、B、C满足
(14)已知平面上三点A、B、C满足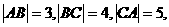 则AB· BC+BC·CA+CA·AB的值等于 .
则AB· BC+BC·CA+CA·AB的值等于 .
(15)设坐标平面内有一个质点从原点出发,沿x轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动质点落在点(3,0)(允许重复过此点)处,则质点不同的运动方法共有 种(用数字作答).
(16)已知平面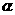 和平面
和平面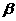 交于直线
交于直线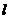 ,P是空间一点,PA⊥
,P是空间一点,PA⊥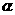 ,垂足为A,PB⊥
,垂足为A,PB⊥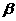 ,垂足为B,且PA=1,PB=2,若点A在
,垂足为B,且PA=1,PB=2,若点A在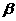 内的射影与点B在
内的射影与点B在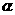 内的射影重合,则点P到
内的射影重合,则点P到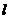 的距离为
.
的距离为
.
22.(本小题满分14分)
椭圆的中心是原点O,它的短轴长为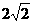 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(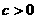 )的准线
)的准线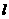 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
(1)求椭圆的方程及离心率;
(2)若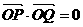 ,求直线PQ的方程;
,求直线PQ的方程;
(3)设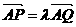 (
(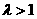 ),过点P且平行于准线
),过点P且平行于准线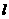 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明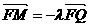 .
.
2004年普通高等学校招生全国统一考试(天津卷)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com