
题目列表(包括答案和解析)
1. (2011山东泰安,11 ,3分)某班为奖励在校运会上取得较好成绩的运动员,花了400元钱购买甲、乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元,求甲乙两种奖品各买多少件?该问题中,若设购买甲种奖品x件,乙种奖品y件,则方程组正确的是( )
A. B. C. D.
[答案]B
19. (2011湖南湘潭市,21,6分)(本题满分6分)
某小区前坪有一块空地,现想建成一块面积大于48平方米,周长小于34米的矩形绿化草地,已知一边长为8米,设其邻边长为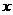 米,求
米,求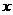 的整数解.
的整数解.
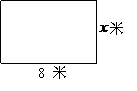

[答案]解:依题意得: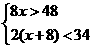 ,解得:6<x<9,当
,解得:6<x<9,当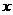 为整数时,则取值为:7、8.
为整数时,则取值为:7、8.
18. (2011山东枣庄,22,8分)某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
解:(1)设组建中型图书角x个,则组建小型图书角为(30-x)个.由题意,得
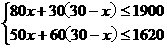 ……………………………………2分
……………………………………2分
解这个不等式组,得18≤x≤20.
由于x只能取整数,∴x的取值是18,19,20.
当x=18时,30-x=12;当x=19时,30-x=11;当x=20时,30-x=10.
故有三种组建方案:方案一,中型图书角18个,小型图书角12个;方案二,中型图书
角19个,小型图书角11个;方案三,中型图书角20个,小型图书角10个. …5分
(2)方案一的费用是:860×18+570×12=22320(元);
方案二的费用是:860×19+570×11=22610(元);
方案三的费用是:860×20+570×10=22900(元).
故方案一费用最低,最低费用是22320元. ……………………………………8分
17. (2011贵州安顺,24,10分)某班到毕业时共结余班费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件T恤或一本影集作为纪念品.已知每件T恤比每本影集贵9元,用200元恰好可以买到2件T恤和5本影集.
⑴求每件T恤和每本影集的价格分别为多少元?
⑵有几种购买T恤和影集的方案?
[答案](1)设T恤和影集的价格分别为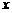 元和
元和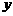 元.则
元.则
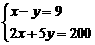
解得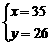
答:T恤和影集的价格分别为35元和26元.
(2)设购买T恤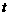 件,则购买影集 (50-
件,则购买影集 (50-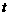 )
本,则
)
本,则
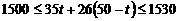
解得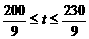 ,∵
,∵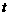 为正整数,∴
为正整数,∴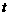 = 23,24,25,
= 23,24,25,
即有三种方案.第一种方案:购T恤23件,影集27本;
第二种方案:购T恤24件,影集26本;
第三种方案:购T恤25件,影集25本.
0.1(x-10)=20-16,解这个方程得x=50;
答:一次至少买50只,才能以最低价购买.
(2) 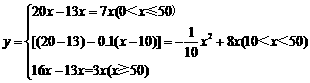 .
.
(说明:因三段图象首尾相连,所以端点10、50包括在哪个区间均可)
(3)将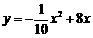 配方得
配方得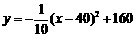 ,所以店主一次卖40只时可获得最高利润,最高利润为160元.(也可用公式法求得)
,所以店主一次卖40只时可获得最高利润,最高利润为160元.(也可用公式法求得)
16. (2011山东菏泽,20,9分)我市一家电子计算器专卖店每只进价13元,售价20元,多买优惠 ;凡是一次买10只以上的,每多买1只,所买的全部计算器每只就降低0.10元,例如,某人买20只计算器,于是每只降价0.10×(20-10)=1(元),因此,所买的全部20只计算器都按照每只19元计算,但是最低价为每只16元.
(1) 求一次至少买多少只,才能以最低价购买?
(2) 写出该专卖店当一次销售x(时,所获利润y(元)与x(只)之间的函数关系式,并写出自变量x的取值范围;
(3)若店主一次卖的只数在10至50只之间,问一次卖多少只获得的利润最大?其最大利润为多少?
解:(1)设一次购买x只,才能以最低价购买,则有:
15. (2011湖北鄂州,20,8分)今年我省干旱灾情严重,甲地急需要抗旱用水15万吨,乙地13万吨.现有A、B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.
⑴设从A水库调往甲地的水量为x万吨,完成下表


|
甲 |
乙 |
总计 |
||||||
|
A |
x |
|
14 |
||||||
|
B |
|
|
14 |
||||||
|
总计 |
15 |
13 |
28 |
⑵请设计一个调运方案,使水的调运量尽可能小.(调运量=调运水的重量×调运的距离,单位:万吨•千米)
[答案]⑴(从左至右,从上至下)14-x 15-x x-1
⑵y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275
解不等式1≤x≤14
所以x=1时y取得最小值
ymin=1280
14. (2011重庆市潼南,25,10分)潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两
种植户种植的两类蔬菜的种植面积与总收入如下表:
|
种植户 |
种植A类蔬菜面积 (单位:亩) |
种植B类蔬菜面积 (单位:亩) |
总收入 (单位:元) |
|
甲 |
3 |
1 |
12500 |
|
乙 |
2 |
3 |
16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
⑴ 求A、B两类蔬菜每亩平均收入各是多少元?
⑵ 某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
[答案]解:(1)设A、B两类蔬菜每亩平均收入分别是x元,y元.
由题意得: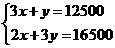 ----------------3分
----------------3分
解得: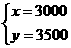
答:A、B两类蔬菜每亩平均收入分别是3000元,3500元.----5分
(2)设用来种植A类蔬菜的面积a亩,则用来种植B类蔬菜的面积为(20-a)亩.
由题意得: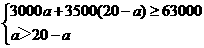 ----------7分
----------7分
解得:10<a≤14.
∵a取整数为:11、12、13、14. ----------------------------8分
∴租地方案为:
|
类别 |
种植面积 单位:(亩) |
|||
|
A |
11 |
12 |
13 |
14 |
|
B |
9 |
8 |
7 |
6 |
---------------------------10分
13. (2011内蒙古乌兰察布,23,10分),某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个,摆放在迎宾大道两侧.已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆.
(l)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
[答案]⑴设搭建A种园艺造型x个,则搭建B种园艺造型(50-x)个.
根据题意得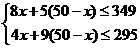 解得
解得 ,
,
所以共有三种方案①A :31 B:19
②A :32 B:18
③A :33 B:17
⑵由于搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,所以搭配同样多的园艺造型A种比B种成本低,则应该搭配A种33个,B种17个.
成本:33×200+17×360=12720(元)
说明:也可列出成本和搭配A种造型数量x之间的函数关系,用函数的性质求解;或直接算出三种方案的成本进行比较也可.
12. (2011广东茂名,23,8分)某养鸡场计划购买甲、乙两种小鸡苗共2 000只进行饲养,已知甲种小鸡苗每只2元,乙种小鸡苗每只3元.
(1)若购买这批小鸡苗共用了4 500元,求甲、乙两种小鸡苗各购买了多少只? (2分)
(2)若购买这批小鸡苗的钱不超过4 700元,问应选购甲种小鸡苗至少多少只? (3分)
(3)相关资料表明:甲、乙两种小鸡苗的成活率分别为94%和99%,若要使这批小鸡苗的成活率不低于96%且买小鸡的总费用最小,问应选购甲、乙两种小鸡苗各多少只?总费用最小是多少元? (3分)
[答案]解: 设购买甲种小鸡苗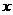 只,那么乙种小鸡苗为(200-
只,那么乙种小鸡苗为(200-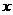 )只.
)只.
(1)根据题意列方程,得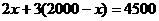 ,
,
解这个方程得: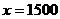 (只),
(只),
 (只),·即:购买甲种小鸡苗1500只,乙种小鸡苗500只.
(只),·即:购买甲种小鸡苗1500只,乙种小鸡苗500只.
(2)根据题意得: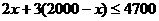 ,
,
解得: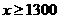 ,
,
即:选购甲种小鸡苗至少为1300只.
(3)设购买这批小鸡苗总费用为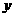 元,
元,
根据题意得: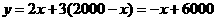 ,
,
又由题意得: ,
,
解得: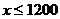 ,
,
因为购买这批小鸡苗的总费用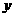 随
随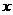 增大而减小,所以当
增大而减小,所以当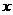 =1200时,总费用
=1200时,总费用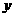 最小,乙种小鸡为:2000-1200=800(只),即:购买甲种小鸡苗为1200只,乙种小鸡苗为800只时,总费用
最小,乙种小鸡为:2000-1200=800(只),即:购买甲种小鸡苗为1200只,乙种小鸡苗为800只时,总费用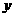 最小,最小为4800元.
最小,最小为4800元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com