
题目列表(包括答案和解析)
2.难点:加强数学应用意识,提高分析问题,解决问题的能力
1.重点:会用向量方法解决简单的力学问题与其他一些实际问题,如确定力或速度的大小以及方向.
3.
重要不等式: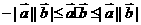
特别提醒: 常用于求参数的范围
★ 重 难 点 突 破 ★
2.平面向量在物理中的应用
如图5-4-3所示,一物体在力F的作用下产生位移S,
(6) 那么力F所做的功: W= |F| |S| cosα.
1. 利用向量处理几何问题的步骤为:
(1) 建立平面直角坐标系;
(2) 设点的坐标;
(3) 求出有关向量的坐标;
(4) 利用向量的运算计算结果;
(5)
 得到结论.
得到结论.
21.(本题满分12分)已知向量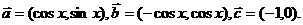
(1)若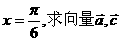 的夹角;
的夹角;
(2)当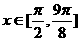 时,求函数
时,求函数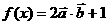 的最大值。
的最大值。
解:(1)当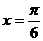 时,
时,
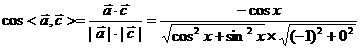 ………………2分
………………2分
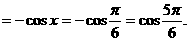 ………………3分
………………3分
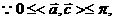
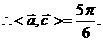 ……………………5分
……………………5分
(2)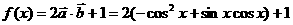 …………7分
…………7分
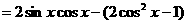
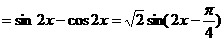 ……………………9分
……………………9分
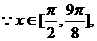
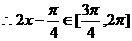 ……………………10分
……………………10分
故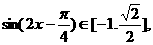
∴当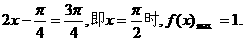 ……………………12分
……………………12分
20.(本题满分14分)在平面直角坐标系中,O为坐标原点,已知向量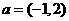 ,又点
,又点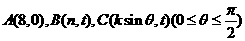
(1)若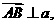 且
且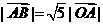 ,求向量
,求向量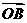 ;
;
(2)若向量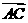 与向量
与向量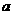 共线,当
共线,当 时,且
时,且 取最大值为4时,求
取最大值为4时,求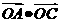
解: 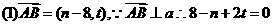 ……2分
……2分
又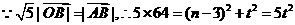 ,得
,得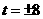 ……4分
……4分
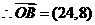 或
或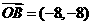 ……6分
……6分
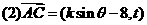
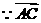 与
与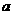 向量共线,
向量共线, 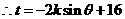 ……8分
……8分
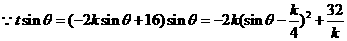
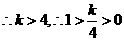 ,
, 当
当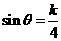 时,
时, 取最大值为
取最大值为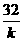 (10分)
(10分)
由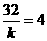 ,得
,得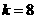 ,此时
,此时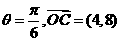 ……12分
……12分
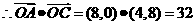 (14分)
(14分)
19.(本题满分14分)已知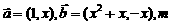 为实数,
为实数,
求使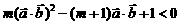 成立的x的范围.
成立的x的范围.
解: 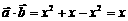
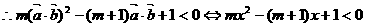 ………4分
………4分
10当m=0时,x>1…………………6分
20当m≠0时,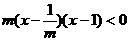
①m<0时,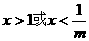 …………………8分
…………………8分
②0<m<1时,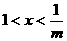 ……………10分
……………10分
③m=1时, x 不存在………………………12分
④m>1时,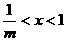 ……………………………14分
……………………………14分
18.(本题满分14分)已知向量a是以点A(3,-1)为起点,且与向量b=(-3,4)垂直的单位向量,求a的终点坐标
解:设a的终点坐标为(m,n)……1分
则a=(m-3,n+1)……3分
|
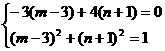 ……6分
……6分
由①得:n=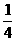 (3m-13)代入②得……7分
(3m-13)代入②得……7分
25m2-15Om+2O9=O ……9分
解得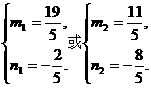 ……13分
……13分
∴a的终点坐标是(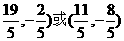 ……14分
……14分
17.(本题满分13分)已知开口向上的二次函数f(x),对任意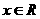 ,恒有
,恒有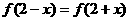 成立,设向量
成立,设向量
a=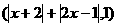 ,b=(1,2)。求不等式f(a·b)<f(5)的解集。
,b=(1,2)。求不等式f(a·b)<f(5)的解集。
由题意知f(x)在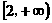 上是增函数,…(1分)
上是增函数,…(1分)
 a·b=
a·b=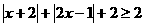 …(2分)
…(2分)
 f(a·b)<f(5)
f(a·b)<f(5) a·b<5
a·b<5
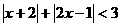 (*) …(3分)
(*) …(3分)
①
当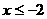 时,不等式(*)可化为
时,不等式(*)可化为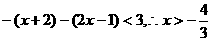 ,…(5分)
,…(5分)
此时x无解;…(6分)
②
当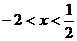 时,不等式(*)可化为
时,不等式(*)可化为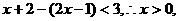 …(8分)
…(8分)
此时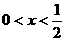 ;…(9分)
;…(9分)
③
当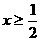 时,不等式(*)可化为
时,不等式(*)可化为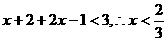 ,…(11分)
,…(11分)
此时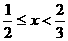 。…(12分)
。…(12分)
综上可知:不等式f(a·b)<f(5)的解集为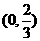 。…(13分)
。…(13分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com