
题目列表(包括答案和解析)
19、(2011•临沂)如图,上面各图都是用全等的等边三角形拼成的一组图形.则在第10个这样的图形中共有 100 个等腰梯形.
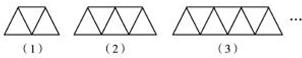
考点:规律型:图形的变化类。
专题:规律型。
分析:由图形可知,第10个图形中有21个等边三角形,再按照一定的顺序找到等腰梯形相加即可.
解答:解:观察图形可知第10个图形中有21个等边三角形,
按照从左往右的顺序可得等腰梯形的个数为:10+9+9+8+8+7+7+6+6+5+5+4+4+3+3+2+2+1+1=100.
故答案为:100.
点评:本题考查了规律型:图形的变化,解题的关键是按照一定的顺序依次找到符合条件的等腰梯形,做到不重复不遗漏.
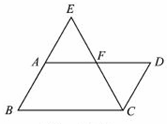
18、(2011•临沂)如图,▱ABCD,E是BA延长线上一点,AB=AE,连接CE交AD于点F,若CF平分∠BCD,AB=3,则BC的长为 6 .
考点:平行四边形的性质;等腰三角形的判定与性质。
分析:平行四边形的对边平行,AD∥BC,AB=AE,所以BC=2AF,若CF平分∠BCD,可证明AE=AF,从而可求出结果.
解答:解:∵若CF平分∠BCD,
∴∠BCE=∠DCF,
∵AD∥BC,
∴∠BCE=∠DFC,
∴∠BCE=∠EFA,
∵BE∥CD,
∴∠E=∠DCF,
∴∠E=∠EFA,
∴AE=AF=AB=3,
∵AB=AE,AF∥BC,
∴BC=2AF=6.
故答案为:6.
点评:本题考查平行四边形的性质,平行四边形的对边平行,以等腰三角形的判定和性质.
17、(2011•临沂)有3人携带会议材料乘坐电梯,这3人的体重共210kg.毎梱材料重20kg.电梯最大负荷为1050kg,则该电梯在此3人乘坐的情况下最多还能搭载 42 捆材枓.
考点:一元一次不等式的应用。
专题:应用题。
分析:可设最多还能搭载x捆材枓,根据电梯最大负荷为1050kg,列出不等式求解即可.
解答:解:设最多还能搭载x捆材枓,依题意得:
20x+210≤1050,
解得:x≤42.
故该电梯在此3人乘坐的情况下最多还能搭载 42捆材枓.
故答案为:42.
点评:本题考查了一元一次不等式的应用,解题的关键是理解电梯最大负荷的含义.
16、(2011•临沂)方程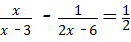 的解是 x=﹣2 .
的解是 x=﹣2 .
考点:解分式方程。
专题:方程思想。
分析:观察可得最简公分母是2(x﹣3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答:解:方程的两边同乘2(x﹣3),得
2x﹣1=x﹣3,
解得x=﹣2.
检验:当x=﹣2时,2(x﹣3)=﹣10≠0.
∴原方程的解为:x=﹣2.
故答案为:x=﹣2.
点评:考查了解分式方程,注意:
(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
15、(2011•临沂)分解因式:9a﹣ab2= a(3+b)(3﹣b) .
考点:提公因式法与公式法的综合运用。
专题:因式分解。
分析:先提取公因式a,再根据平方差公式进行二次分解.
解答:解:9a﹣ab2=a(9﹣b2)=a(3+b)(3﹣b).
故答案为:a(3+b)(3﹣b).
点评:本题考查了提公因式法,公式法分解因式.注意分解要彻底.
14、(2011•临沂)甲、乙两同学同时从400m环形跑道上的同一点出犮,同向而行.甲的速度为6m/s,乙的速度为4m/s.设经过x(单位:s)后,跑道上此两人间的较短部分的长度为y(单位:m).则y与x(0≤x≤300)之间的函数关系可用图象表示为( )
A、 B、
B、
C、 D、
D、
考点:函数的图象。
专题:计算题。
分析:由于相向而行,且二人速度差为6﹣4=2m/s,二人间最长距离为200米,最短距离为0,据此即可进行推理.
解答:解:二人速度差为6﹣4=2m/s,
100秒时,二人相距2×100=200米,
200秒时,二人相距2×200=400米,较短部分的长度为0,
300秒时,二人相距2×300=600米,即甲超过乙600﹣400=200米.
由于y=2x或y=400﹣2x,函数图象为直线(线段).
故选C.
点评:本题考查利用函数的图象解决实际问题,正确理解函数图象表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.
13、(2011•临沂)如图,△ABC中,cosB=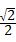 ,sinC=
,sinC=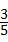 ,AC=5,则△ABC的面积是( )
,AC=5,则△ABC的面积是( )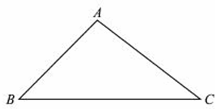
A、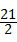 B、12
B、12
C、14 D、21
考点:解直角三角形。
分析:根据已知做出三角形的高线AD,进而得出AD,BD,CD,的长,即可得出三角形的面积.
解答:解:过点A做AD⊥BC,
∵△ABC中,cosB=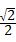 ,sinC=
,sinC=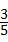 ,AC=5,
,AC=5,
∴cosB=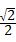 =
=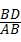 ,
,
∴∠B=45°,
∵sinC=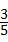 =
=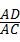 =
=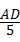 ,
,
∴AD=3,
∴CD=4,
∴BD=3,
则△ABC的面积是: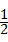 ×AD×BC=
×AD×BC=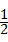 ×3×(3+4)=
×3×(3+4)=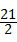 .
.
故选A.
点评:此题主要考查了解直角三角形的知识,做出AD⊥BC,进而得出相关线段的长度是解决问题的关键.
12、(2011•临沂)如图,梯形ABCD中,AD∥BC,AB=CD.AD=2,BC=6,∠B=60°,则梯形ABCD的周长是( )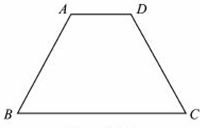
A、12 B、14
C、16 D、18
考点:等腰梯形的性质;含30度角的直角三角形。
分析:从上底的两个端点向下底作垂线,构造直角三角形和矩形,求得直角三角形的直角边的长利用告诉的锐角的度数求得等腰梯形的腰长,然后求得等腰梯形的周长.
解答:解:作AE⊥BC于E点,DF⊥BC于F点,
∵AD∥BC,
∴四边形AEFD为矩形,
∵AD=2,BC=6,
∴EF=AD=2,BE=CF=(6﹣2)÷2=2,
∵∠B=60°,
∴AB=DC=2BE=2×2=4,
∴等腰梯形的周长为:AB+BC+CD+DA=4+6+4+2=16.
故选C.

点评:本题考查了等腰梯形的性质及含30°的直角三角形的性质,解题的关键是正确的作辅助线构造直角三角形和矩形,从而求得等腰梯形的高.
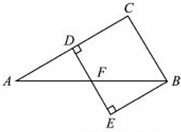
11、(2011•临沂)如图.△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
A、2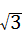 B、3
B、3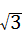
C、4 D、4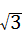
考点:矩形的判定与性质;线段垂直平分线的性质;勾股定理。
分析:因为DE是AC的垂直的平分线,所以D是AC的中点,F是AB的中点,所以DF∥BC,所以∠C=90°,所以四边形BCDE是矩形,因为∠A=30°,∠C=90°,BC=2,能求出AB的长,根据勾股定理求出AC的长,从而求出DC的长,从而求出面积.
解答:解:∵DE是AC的垂直的平分线,F是AB的中点,
∴DF∥BC,
∴∠C=90°,
∴四边形BCDE是矩形.
∵∠A=30°,∠C=90°,BC=2,,
∴AB=4,
∴AC=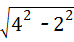 =2
=2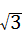 .
.
∴DE=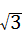 .
.
∴四边形BCDE的面积为:2×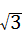 =2
=2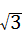 .
.
故选A.
点评:本题考查了矩形的判定定理,矩形的面积的求法,以及中位线定理,勾股定理,线段垂直平分线的性质等.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com