
题目列表(包括答案和解析)
3.解:(1)当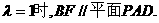 (1分)
(1分)
证明:取PD中点E,则EF//CD,且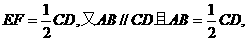
∴四边形ABFE为平行四边形. (3分)
∴BF//AE. 又AE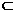 平面PAD ∴BF//平面PAD (4分)
平面PAD ∴BF//平面PAD (4分)
(2)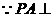 平面ABCD,
平面ABCD,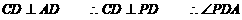 即是二面角的平
即是二面角的平
面角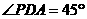 (5分)
(5分)
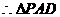 为等腰直角三角形,
为等腰直角三角形,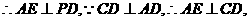
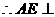 平面PCD 又BF//AE,
平面PCD 又BF//AE,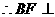 平面PCD.
平面PCD. 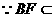 平面PBC,
平面PBC,
∴平面PCD⊥平面PBC,即二面角B-PC-D的大小为90°. (8分)
(3)在平面PCD内作EH⊥PC于点H,由平面PCD⊥平面PBC且平面PCD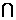
平面PBC=PC知:EH⊥平面PBC. (9分)
在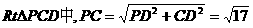 ,
,
在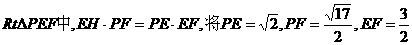 代入得:
代入得:
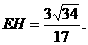 即点E到平面PBC的距离为
即点E到平面PBC的距离为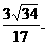 (11分)
(11分)
又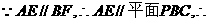 点A到平面PBC的距离为
点A到平面PBC的距离为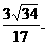 (12分)
(12分)
3.[哈尔滨三中东北育才大连育明 天津耀华2005年四校高考模拟联考]
如图已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,AB=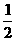 CD.
CD.
(I)点F在线段PC上运动,且设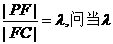 为何值时,BF//平面PAD?并证明你的结论;
为何值时,BF//平面PAD?并证明你的结论;
(Ⅱ)二面角F-CD-B为45°,求二面角B-PC-D的大小;
(Ⅲ)在(Ⅱ)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.
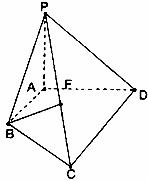
2. 解:(1)取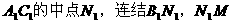
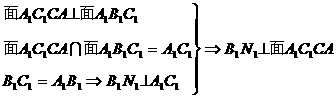
 …………3分
…………3分
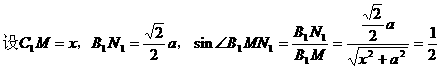
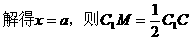
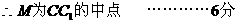
(2)取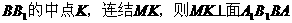
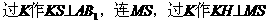
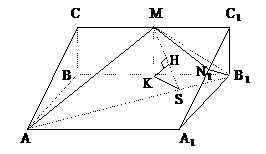
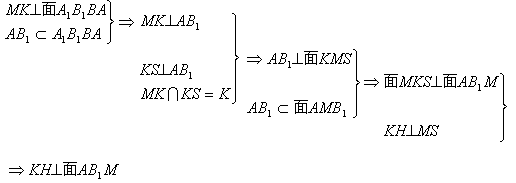
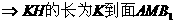 的距离,由
的距离,由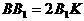 ,则B到面
,则B到面 的距离为K到面
的距离为K到面 的距离的2倍 …………9分
的距离的2倍 …………9分
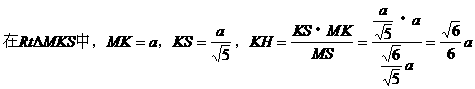

另法一:利用体积相等,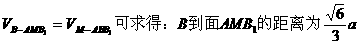
另法二:可利用面
2.[哈师大附中、东北师大附中、辽宁省实验中学2005年高三第二次联合考试数学试卷(理科)]
已知直三棱柱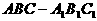 中,
中,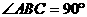 ,AB=BC=a,
,AB=BC=a,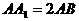 ,M为
,M为 上的点。
上的点。
(1)当M在 上的什么位置时,
上的什么位置时,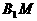 与平面
与平面 所成的角为
所成的角为 ;
;
(2)在(1)的条件下求B到平面 的距离。
的距离。
1.解:(I)
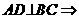 异面直线AD、BC所成角为
异面直线AD、BC所成角为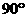 。 4分
。 4分
(II)过点P作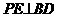 于E,过点E作
于E,过点E作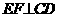 于F,连结PF。
于F,连结PF。

8分
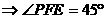 。
。
设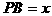 ,则在
,则在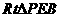 中,
中,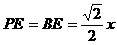 ,
,
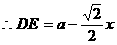
在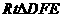 中,
中,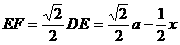
在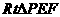 中,
中,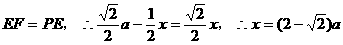
11分
即P、B两点间距离为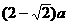 时,
时, 与
与 所在平面成
所在平面成 角。 12分
角。 12分
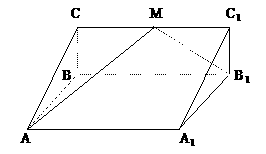
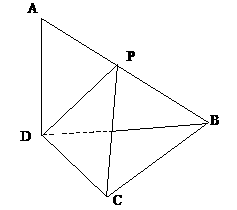
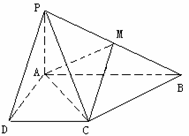
1.[2005年山东省临沂市数学模拟试题(文史类)]
如图所示,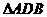 和
和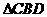 都是等腰直角三角形,且它们所在的平面互相垂直,
都是等腰直角三角形,且它们所在的平面互相垂直,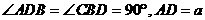
(I)求异面直线AD、BC所成的角。
(II)设P是线段AB上的动点,问P、B两点间的距离多少时? 与
与 所在平面成
所在平面成 角;
角;
24.(本小题满分12分) (2005年高考·全国卷Ⅲ·理18文19)
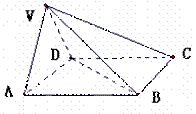 如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(Ⅰ)证明AB⊥平面VAD;
(Ⅱ)求面VAD与面VDB所成的二面角的大小.
证明:方法一:(Ⅰ)证明:
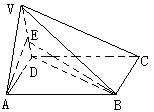
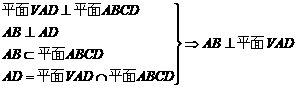
(Ⅱ)解:取VD的中点E,连结AF,BE,
∵△VAD是正三形,
∴AE⊥VD,AE=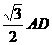
∵AB⊥平面VAD, ∴AB⊥AE.
又由三垂线定理知BE⊥VD. 因此,tan∠AEB=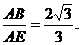
即得所求二面角的大小为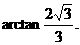
方法二:以D为坐标原点,建立如图所示的坐标图系.
(Ⅰ)证明:不防设作A(1,0,0),
则B(1,1,0), 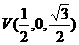 ,
,
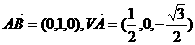
由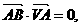 得AB⊥VA. 又AB⊥AD,因而AB与平面VAD内两条相交直线VA,AD都垂直. ∴AB⊥平面VAD.
得AB⊥VA. 又AB⊥AD,因而AB与平面VAD内两条相交直线VA,AD都垂直. ∴AB⊥平面VAD.
(Ⅱ)解:设E为DV中点,则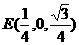 ,
,
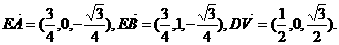
由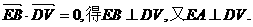
因此,∠AEB是所求二面角的平面角,
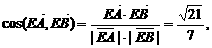
解得所求二面角的大小为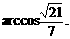
23.(本小题满分12分)(2005年高考·全国卷II·理20文20))
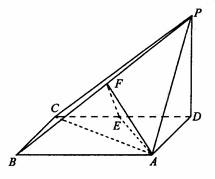 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点.
(Ⅰ)求证:EF⊥平面PAB;
(Ⅱ)设AB=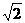 BC,求AC与平面AEF所成的角的大小.
BC,求AC与平面AEF所成的角的大小.
本小题主要考查直线与平面垂直、直线与平面所成角的有关知识、及思维能力和空间想象能力。满分12分。
证明:(Ⅰ)证明:连结EP, 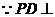 底面ABCD,DE在平面ABCD内,
底面ABCD,DE在平面ABCD内,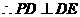 。
。
又CE=ED,PD=AD=BC,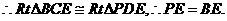
 F为PB中点,∴
F为PB中点,∴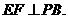 由三垂线定理得
由三垂线定理得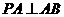 ,∴在
,∴在 中,PF=AF。
中,PF=AF。
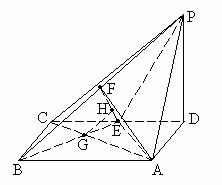 又PE=BE=EA,
又PE=BE=EA,

 PB、FA为平面PAB内的相交直线,∴EF
PB、FA为平面PAB内的相交直线,∴EF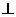 平面PAB。
平面PAB。
(Ⅱ)解:不妨设BC=1,则AD=PD=1,AB=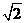 ,PA=
,PA=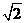 ,AC=
,AC=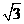
∴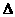 PAB为等腰直角三角形,且PB=2,F为其斜边中点,BF=1,且AF
PAB为等腰直角三角形,且PB=2,F为其斜边中点,BF=1,且AF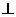 PB。
PB。
 PB与平面AEF内两条相交直线EF、AF都垂直,∴PB
PB与平面AEF内两条相交直线EF、AF都垂直,∴PB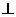 平面AEF。
平面AEF。
连结BE交AC于G,作GH∥BP交EF于H,则GH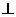 平面AEF,
平面AEF,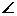 GAH为AC与平面AEF所成的角。
GAH为AC与平面AEF所成的角。
由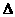 EGC∽
EGC∽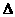 BGA可知EG=
BGA可知EG=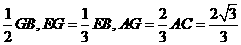 ,
,
由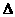 ECH∽
ECH∽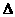 EBF可知
EBF可知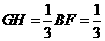 ,
,
∴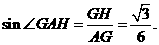
∴ 与平面
与平面 所成的角为
所成的角为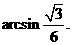
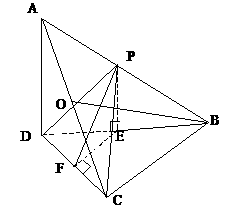
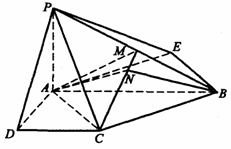
22.(本小题满分12分)(2005年高考·全国卷Ⅰ·理18文18)
 已知四棱锥P-ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DE=
已知四棱锥P-ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DE=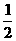 AB=1,M是PB的中点.
AB=1,M是PB的中点.
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角的大小.
本小题主要考查直线与平面垂直、直线与平面所成角的有关知识及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力.满分12分.
方案一:
(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
 ∴由三垂线定理得:CD⊥PD.
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD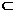 面PCD,∴面PAD⊥面PCD.
面PCD,∴面PAD⊥面PCD.
(Ⅱ)解:过点B作BE//CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连结AE,可知AC=CB=BE=AE=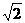 ,又AB=2,
,又AB=2,
所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=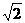 ,PB=
,PB=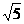 ,
, 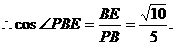

(Ⅲ)解:作AN⊥CM,垂足为N,连结BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角.
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN·MC=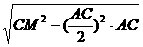 ,
,
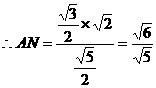 . ∴AB=2,
. ∴AB=2,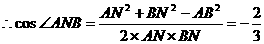
故所求的二面角为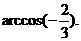
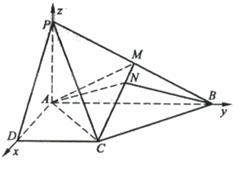
方法二:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为
A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,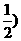 .
.
(Ⅰ)证明:因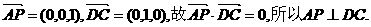
由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.
 又DC在面PCD上,故面PAD⊥面PCD.
又DC在面PCD上,故面PAD⊥面PCD.
(Ⅱ)解:因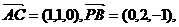

(Ⅲ)解:在MC上取一点N(x,y,z),则存在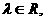 使
使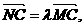
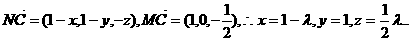
要使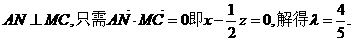
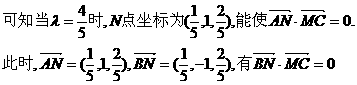
 为所求二面角的平面角.
为所求二面角的平面角.

21.(本小题满分12分)(2005年高考·天津卷·理19文19)
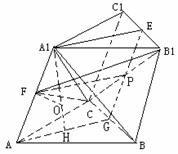
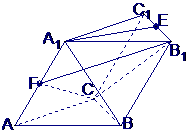 如图,在斜三棱柱
如图,在斜三棱柱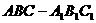 中,
中, ,侧面
,侧面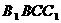 与底面ABC所成的二面角为
与底面ABC所成的二面角为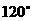 ,E、F分别是棱
,E、F分别是棱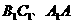 的中点.
的中点.
(Ⅰ)求 与底面ABC所成的角;
与底面ABC所成的角;
(Ⅱ)证明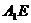 //平面
//平面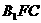 ;
;
(Ⅲ)求经过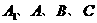 四点的球的体积.
四点的球的体积.
本小题主要考查棱柱、球、二面角、线面关系等基础知识,考查空间想象能力和推理论证能力.满分12分.
 (Ⅰ)解:过A1作A1H⊥平面ABC,垂足为H.
(Ⅰ)解:过A1作A1H⊥平面ABC,垂足为H.
连结AH,并延长交BC于G,连结EG,于是
∠A1AH为A1A与底面ABC所成的角.
∵∠A1AB=∠A1AC, ∴AG为∠BAC的平分线.
又∵AB=AC, ∴AG⊥BC,且G为BC的中点
因此,由三垂线定理,A1A⊥BC.
∵A1A//B1B,且EG//B1B, EG⊥BC 于是
∠AGE为二面角A-BC-E的平面角,即
∠AGE=120°
由于四边形A1AGE为平行四边形,得∠A1AG=60°,
所以,A1A与底面ABC所成的角为60°,
(Ⅱ)证明:设EG与B1C的交点为P,则点P为EG的中点,连结PF.
在平行四边形AGEA1中,因F为A1A的中点,故A1E//FP.
而FP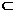 平面B1FC,A1E//平面B1FC,所以A1E//平面B1FC.
平面B1FC,A1E//平面B1FC,所以A1E//平面B1FC.
(Ⅲ)解:连结A1C,在△A1AC和△A1AB中,由于AC=AB,∠A1AC=∠A1AB,
A1A=A1A,则△A1AC≌△A1AB,故A1C=A1B,由已知得 A1A=A1B=A1C=a.
又∵A1H⊥平面ABC, ∴H为△ABC的外心.
设所求球的球心为O,则O∈A1H,且球心O与A1A中点的连线OF⊥A1A.
在Rt△A1FO中, 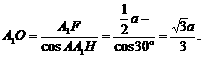
故所求球的半径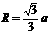 ,球的体积
,球的体积 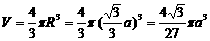
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com