
题目列表(包括答案和解析)
3. (2011福建福州,7,4分)一元二次方程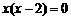 根的情况是( )
根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
[答案]A
2. (2011湖北荆州,9,3分)关于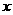 的方程
的方程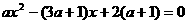 有两个不相等的实根
有两个不相等的实根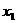 、
、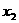 ,且有
,且有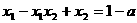 ,则
,则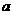 的值是
的值是
A.1 B.-1 C.1或-1 D. 2
[答案]B
1. (2011湖北鄂州,11,3分)下列说法中
①一个角的两边分别垂直于另一个角的两边,则这两个角相等
②数据5,2,7,1,2,4的中位数是3,众数是2
③等腰梯形既是中心对称图形,又是轴对称图形
④Rt△ABC中,∠C=90°,两直角边a,b分别是方程x2-7x+7=0的两个根,则AB边上的中线长为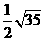
正确命题有( )
A.0个 B.1个 C.2个 D.3个
[答案]C
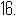 (本小题6分)解方程组
(本小题6分)解方程组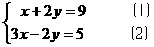
[答案] 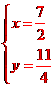
[解析] 由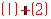 ,得:
,得: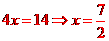 ,把
,把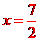 代入
代入 ,得
,得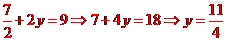
 (本小题8分)先化简
(本小题8分)先化简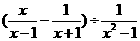 ,再从
,再从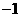 、
、 、
、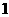 三个数中,选择一个你认为合适的数作为
三个数中,选择一个你认为合适的数作为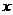 的值代入求值.
的值代入求值.
[答案] 化简得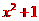 ;取
;取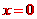 求得值为
求得值为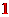 .
.
[解析] 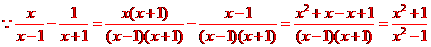
∴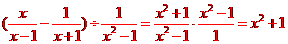
取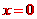 代入,得原式的值为
代入,得原式的值为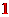 .
.
 (本小题8分)如图,在平行四边形
(本小题8分)如图,在平行四边形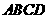 中,点
中,点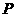 是对角线
是对角线 上的一点,
上的一点,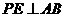 ,
,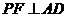 ,垂足分别为
,垂足分别为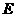 、
、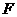 ,且
,且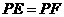 ,平行四边形
,平行四边形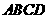 是菱形吗?这什么?
是菱形吗?这什么?
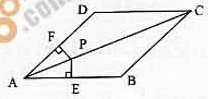 [答案] 平行四边形
[答案] 平行四边形 是菱形.
是菱形.
[解析] 如图,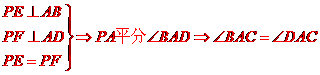
在
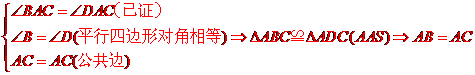
 所以平行四边形
所以平行四边形 的邻边相等,故平行四边形
的邻边相等,故平行四边形 是菱形.
是菱形.
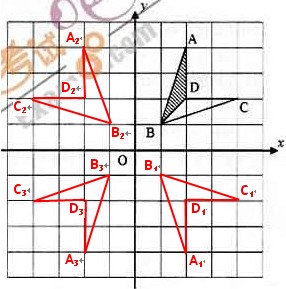
 (本小题8分)如图,下列网格中,每个小方格的边长都是1.
(本小题8分)如图,下列网格中,每个小方格的边长都是1.
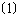 分别作出四边形
分别作出四边形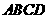 关于
关于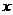 轴、
轴、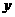 轴、原点的对称图形;
轴、原点的对称图形;
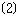 求出四边形
求出四边形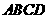 的面积.
的面积.
[答案] 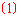 略;
略; .
.
[解析]  如图,四边形
如图,四边形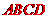 关于
关于 轴、
轴、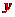 轴、原点的对称图形分别是四边形
轴、原点的对称图形分别是四边形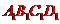 、四边形
、四边形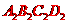 、四边形
、四边形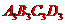 ;
;
 四边形
四边形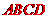 的面积
的面积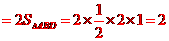
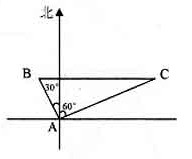
 (本小题8分)如图,甲、乙两船同时从港口
(本小题8分)如图,甲、乙两船同时从港口 出发,甲船以
出发,甲船以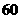 海里/时的速度沿北偏东
海里/时的速度沿北偏东 方向航行,乙船沿北偏西
方向航行,乙船沿北偏西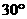 方向航行,半小时后甲船到达
方向航行,半小时后甲船到达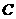 点,乙船正好到达甲船正西方向的
点,乙船正好到达甲船正西方向的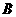 点,求乙船的速度
点,求乙船的速度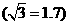 .
.
[答案].  海里/时
海里/时
[解析] 因为甲船航行半小时后到达 点,
点,
所以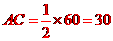 (海里)
(海里)
又,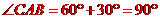 ,
,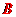 点是
点是 点的正西方向,
点的正西方向,
所以,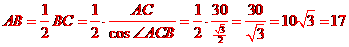 (海里)
(海里)
故,乙船的速度是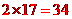 海里/时
海里/时
 (本小题8分)为贯彻落实云南省教育厅提出的“三生教育”,在母亲节来临之际,某校团委组织了以“珍爱生命,学会生存,感恩父母”为主题的教育活动,在学校随机调查了
(本小题8分)为贯彻落实云南省教育厅提出的“三生教育”,在母亲节来临之际,某校团委组织了以“珍爱生命,学会生存,感恩父母”为主题的教育活动,在学校随机调查了 名同学平均每周在家做家务的时间,统计并制作了如下的频数分布和扇形统计图:
名同学平均每周在家做家务的时间,统计并制作了如下的频数分布和扇形统计图:
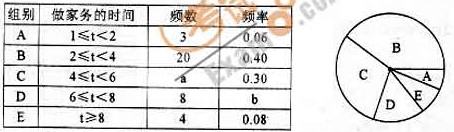
根据上述信息回答下列问题:
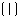
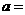 ,
,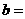 ;
;
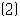 在扇形统计图中,
在扇形统计图中,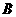 组所占圆心角的度数为 ;
组所占圆心角的度数为 ;
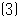 全校共有
全校共有 名学生,估计该校平均每周做家务时间不少于
名学生,估计该校平均每周做家务时间不少于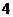 小时的学生约有多少人?
小时的学生约有多少人?
[答案]. 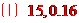 ;
;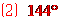 ;
; 约
约 人
人
[解析] 
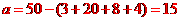 ,
,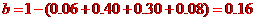 ;
;
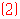 在扇形统计图中,
在扇形统计图中,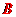 组所占圆心角的度数为
组所占圆心角的度数为 ;
;

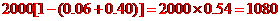 (人)
(人)
该校平均每周做家务时间不少于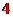 小时的学生约有
小时的学生约有 人
人
 (本小题8分)小华和小丽两人玩数字游戏,先由小丽心中任意想一个数字记为
(本小题8分)小华和小丽两人玩数字游戏,先由小丽心中任意想一个数字记为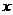 ,再由小华猜小丽刚才想的数字,把小华猜的数字记为
,再由小华猜小丽刚才想的数字,把小华猜的数字记为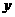 ,且他们想和猜的数字只能在
,且他们想和猜的数字只能在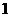 ,
,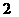 ,
,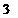 ,
,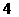 这四个数中.
这四个数中.
 请用树状图或列表法表示了他们想和猜的所有情况;
请用树状图或列表法表示了他们想和猜的所有情况;
 如果他们想和猜的数相同,则称他们“心灵相通”。求他们“心灵相通”的概率;
如果他们想和猜的数相同,则称他们“心灵相通”。求他们“心灵相通”的概率;
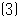 如果他们想和猜的数字满足
如果他们想和猜的数字满足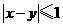 ,则称他们“心有灵犀”。求他们“心有灵犀”的概率;
,则称他们“心有灵犀”。求他们“心有灵犀”的概率;
[答案].  略;
略;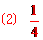 ;
;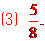
[解析] 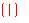 树状图
树状图

列表法
|
想数 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
|
猜数 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
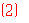 由
由 知道,想和猜的数共有16组,他们“心灵相通”的组有4组,所以,他们“心灵相通”的概率为
知道,想和猜的数共有16组,他们“心灵相通”的组有4组,所以,他们“心灵相通”的概率为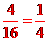
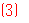 由
由 满足
满足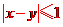 ,即他们“心有灵犀”的数有10组,所以他们“心有灵犀”的概率
,即他们“心有灵犀”的数有10组,所以他们“心有灵犀”的概率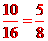
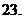 (本小题8分)随着人们节能环保意识的增强,绿色交通工具越来越受到人们的青睐,电动摩托成为人们首选的交通工具,某商场计划用不超过
(本小题8分)随着人们节能环保意识的增强,绿色交通工具越来越受到人们的青睐,电动摩托成为人们首选的交通工具,某商场计划用不超过 元购进
元购进 、
、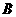 两种不同品牌的电动摩托
两种不同品牌的电动摩托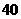 辆,预计这批电动摩托全部销售后可获得不少于
辆,预计这批电动摩托全部销售后可获得不少于 元的利润,
元的利润, 、
、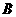 两种品牌电动摩托的进价和售价如下表所示:
两种品牌电动摩托的进价和售价如下表所示:

设该商场计划进 品牌电动摩托
品牌电动摩托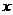 辆,两种品牌电动摩托全部销售后可获利润
辆,两种品牌电动摩托全部销售后可获利润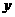 元.
元.
 写出
写出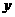 与
与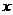 之间的函数关系式;
之间的函数关系式;
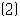 该商场购进
该商场购进 品牌电动摩托多少辆时?获利最大,最大利润是多少?
品牌电动摩托多少辆时?获利最大,最大利润是多少?
[答案]. 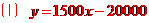 ;
;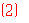
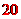 辆,
辆,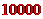 元.
元.
[解析]  该商场计划进
该商场计划进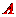 品牌电动摩托
品牌电动摩托 辆,则;进
辆,则;进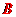 品牌电动摩托
品牌电动摩托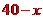 辆,所以
辆,所以

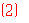
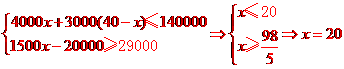 (辆)
(辆)
 (元)
(元)
故,该商场购进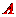 品牌电动摩托
品牌电动摩托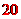 辆时获利最大,最大利润是
辆时获利最大,最大利润是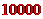 元.
元.
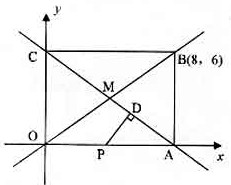
 (本小题13分)如图,四边形
(本小题13分)如图,四边形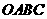 是矩形,点
是矩形,点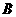 的坐标为
的坐标为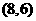 ,直线
,直线 和直线
和直线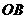 相交于点
相交于点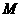 ,点
,点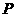 是
是 的中点,
的中点,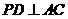 ,垂足为
,垂足为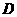 .
.
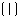 求直线
求直线 的解析式;
的解析式;
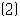 求经过点
求经过点 、
、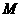 、
、 的抛物线的解析式;
的抛物线的解析式;
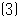 在抛物线上是否存在
在抛物线上是否存在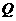 ,使得
,使得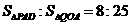 ,若存在,求出点
,若存在,求出点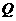 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
[答案]. 
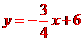 ;
;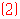
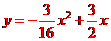 ;
;
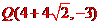 、
、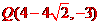 、
、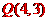
[解析]  如图,易知
如图,易知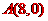 、
、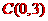 ,设直线
,设直线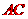 的解析式为:
的解析式为: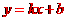 ,则
,则
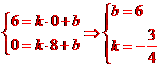 所以,直线
所以,直线 的解析式为
的解析式为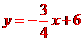
 设经过点
设经过点 、
、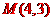 、
、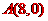 的抛物线的解析式为:
的抛物线的解析式为: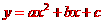 ,则
,则
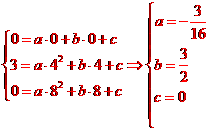 ,所以经过点
,所以经过点 、
、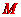 、
、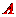 的抛物线的解析式为:
的抛物线的解析式为: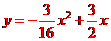
 设存在点
设存在点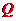 ,坐标为
,坐标为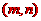 ,则
,则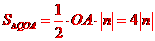
又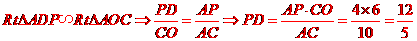 ,
,
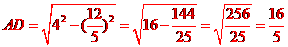 ,所以,
,所以,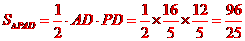
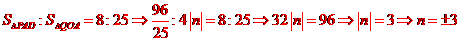
把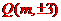 分别代入
分别代入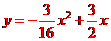 ,得
,得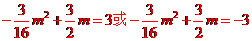
由: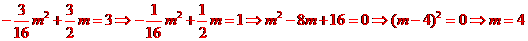
由: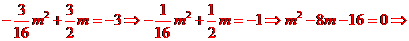
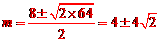
所以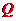 的坐标为:
的坐标为: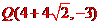 、
、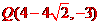 、
、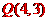
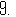 第六次全国人口普查结果公布:云南省常住人口约为
第六次全国人口普查结果公布:云南省常住人口约为 人,这个数据用科学记数法可表示
人,这个数据用科学记数法可表示
为 人.
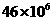
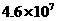
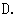
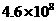
[答案] 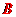
[解析] 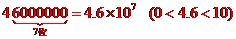 ,故选
,故选
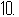 下列运算,结果正确的是
下列运算,结果正确的是
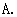
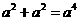
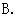
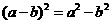
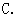
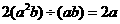
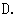
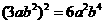
[答案] 
[解析] 因为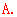
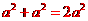 ,
,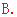
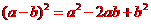 ,
,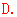
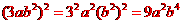

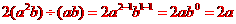 ,故选
,故选
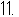 下面几何体的俯视图是
下面几何体的俯视图是
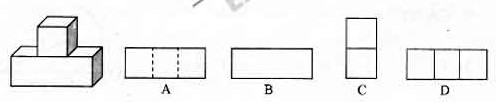
[答案] 
[解析] 俯视能见的图形是三个排成一排的三个正方形,故选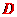
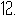 为了庆祝建党
为了庆祝建党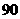 周年,某单位举行了“颂党”歌咏比赛,进入决赛的
周年,某单位举行了“颂党”歌咏比赛,进入决赛的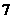 名选手的成绩分别是:
名选手的成绩分别是: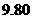 ,
,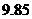 ,
,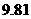 ,
,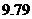 ,
,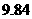 ,
, ,
,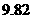 (单位:分),这组数据的中位数和平均数是
(单位:分),这组数据的中位数和平均数是
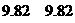
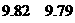
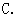
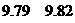
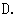
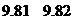
[答案] 
[解析] 计算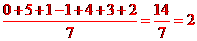 ,平均数是
,平均数是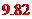 ,故排除
,故排除 、
、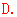 ,又
,又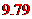 是七个数中最小的数不可以是中位数,故排除
是七个数中最小的数不可以是中位数,故排除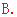 ,所以选
,所以选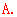
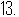 据调查,某市2011年的房价为
据调查,某市2011年的房价为 元/
元/ ,预计2013年将达到
,预计2013年将达到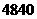 元/
元/ ,求这两年的年平均增长率,设年平均增长率为
,求这两年的年平均增长率,设年平均增长率为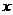 ,根据题意,所列方程为
,根据题意,所列方程为
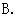
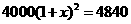
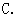
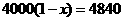
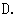
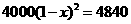
[答案] 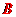
[解析] 一年后,即2012年该市的房价是
两年后,即2013年该市的房价是
所以,根据题意,所列方程为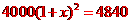 ,故选
,故选
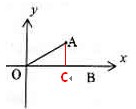
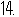 如图,已知
如图,已知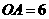 ,
,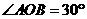 ,则经过点
,则经过点 的反比例函数的解析式为
的反比例函数的解析式为
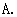
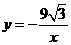
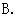
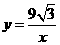
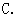
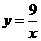
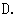
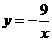
[答案] 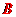
 [解析] 如图,过
[解析] 如图,过 作
作 ,垂足是
,垂足是 ,
,
在 ,
,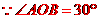 ,
,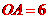
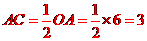 ,
,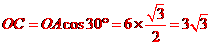
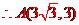 ,由
,由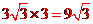 ,得经过点
,得经过点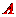 的反比例函数的解析式为
的反比例函数的解析式为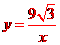 ,故选
,故选
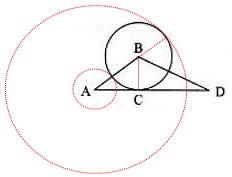
 如图,已知
如图,已知 与
与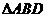 的边
的边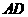 相切于点
相切于点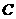 ,
,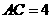 ,
,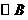 的半径为
的半径为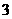 ,当
,当 与
与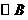 相切时,
相切时, 的半径是
的半径是
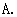
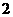
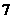
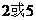
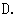

[答案] 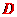
[解析] 如图,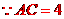 ,
,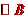 的半径为
的半径为 ,
,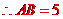
 与
与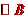 相切有内切和外切两种情况,内切时,半径为
相切有内切和外切两种情况,内切时,半径为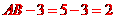 ,外切时,半径为
,外切时,半径为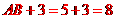 ,故选
,故选
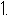
 的相反数是
.
的相反数是
.
[答案] 
[解析]负数的相反数是正数,所以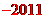 的相反数是是
的相反数是是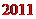
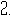 如图,
如图,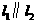 ,
,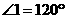 ,则
,则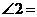 .
.
[答案] 
[解析] 如图,平角定义

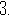 在函数
在函数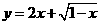 中,自变量
中,自变量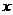 的取值范围是
.
的取值范围是
.
[答案] 
[解析] 由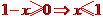
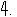 计算
计算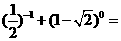 .
.
[答案] 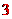
[解析] 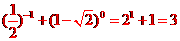
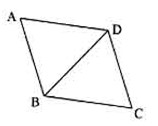
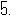 如图,在菱形
如图,在菱形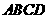 中,
中,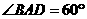 ,
,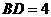 ,则菱形
,则菱形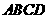 的周长是
.
的周长是
.
[答案] 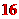
[解析] 菱形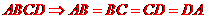 ,又
,又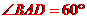 ,
,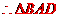 是正三角形,故菱形
是正三角形,故菱形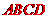 的周长是:
的周长是: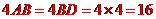
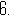 如图,
如图, 的半径是
的半径是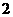 ,
,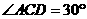 ,则
,则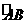 的长是
(结果保留
的长是
(结果保留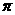 ).
).
[答案] 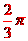
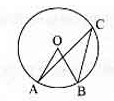 [解析] 如图,因为
[解析] 如图,因为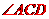 、
、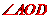 同是
同是 对的圆周角和圆心角,所以
对的圆周角和圆心角,所以
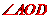
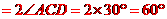
故,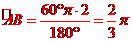
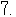 已知
已知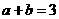 ,
,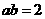 ,则
,则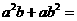 .
.
[答案] 
[解析] 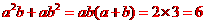
 下面是按一定规律排列的一列数:
下面是按一定规律排列的一列数:
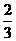 ,
,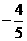 ,
,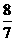 ,
,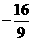 ,
,
那么第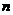 个数是
.
个数是
.
[答案] 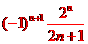
[解析] 由于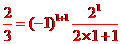 ,
,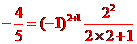 ,
,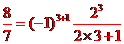
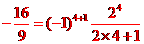 ,
, 那么第
那么第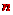 个数是
个数是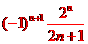
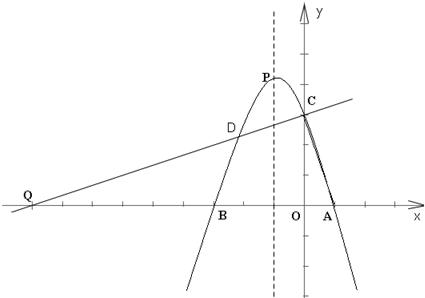
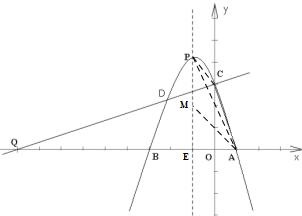
23、(2011•达州)如图,已知抛物线与x轴交于A(1,0),B(﹣3,0)两点,与y轴交于点C(0,3),抛物线的顶点为P,连接AC.
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,且直线DC与x轴交于点Q,求点D的坐标;
(3)抛物线对称轴上是否存在一点M,使得S△MAP=2S△ACP,若存在,求出M点坐标;若不存在,请说明理由.
考点:二次函数综合题。
分析:(1)利用交点式将抛物线与x轴交于A(1,0)、B(﹣3,0)两点,代入y=a(x﹣x1)(x﹣x2),求出二次函数解析式即可;
(2)利用△QOC∽△COA,得出QO的长度,得出Q点的坐标,再求出直线DC的解析式,将两函数联立求出交点坐标即可;
(3)首先求出二次函数顶点坐标,S四边形AEPC=S四边形OEPC+S△AOC,以及S四边形AEPC=S△AEP+S△ACP=得出使得S△MAP=2S△ACP点M的坐标.
解答:解:(1)设此抛物线的解析式为:y=a(x﹣x1)(x﹣x2),
∵抛物线与x轴交于A(1,0)、B(﹣3,0)两点,
∴y=a(x﹣1)(x+3),
又∵抛物线与y轴交于点C(0,3),
∴a(0﹣1)(0+3)=3,
∴a=﹣3
∴y=﹣(x﹣1)(x+3),
即y=﹣x2﹣2x+3,
用其他解法参照给分;
(2)∵点A(1,0),点C(0,3),
∴OA=1,OC=3,
∵DC⊥AC,OC⊥x轴,
∴△QOC∽△COA,
∴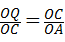 ,即
,即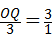 ,
,
∴OQ=9,,
又∵点Q在x轴的负半轴上,
∴Q(﹣9,0),
设直线DC的解析式为:y=mx+n,则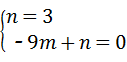 ,
,
解之得: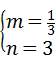 ,
,
∴直线DC的解析式为: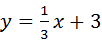 ,
,
∵点D是抛物线与直线DC的交点,
∴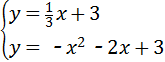 ,
,
解之得: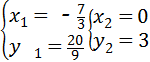 (不合题意,应舍去),
(不合题意,应舍去),
∴点D(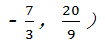 ,
,
用其他解法参照给分;
(3)如图,点M为直线x=﹣1上一点,连接AM,PC,PA,
设点M(﹣1,y),直线x=﹣1与x轴交于点E,
∴AE=2,
∵抛物线y=﹣x2﹣2x+3的顶点为P,对称轴为x=﹣1,
∴P(﹣1,4),
∴PE=4,
则PM=|4﹣y|,
∵S四边形AEPC=S四边形OEPC+S△AOC,
=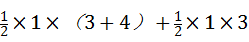 ,
,
=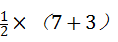 ,
,
=5,
又∵S四边形AEPC=S△AEP+S△ACP,
S△AEP=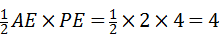 ,
,
∴+S△ACP=5﹣4=1,
∵S△MAP=2S△ACP,
∴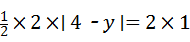 ,
,
∴|4﹣y|=2,
∴y1=2,y2=6,
故抛物线的对称轴上存在点M使S△MAP=2S△ACP,
点M(﹣1,2)或(﹣1,6).
点评:此题主要考查了二次函数的综合应用,二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.
22、(2011•达州)我市化工园区一化工厂,组织20辆汽车装运A、B、C三种化学物资共200吨到某地.按计划20辆汽车都要装运,每辆汽车只能装运同一种物资且必须装满.请结合表中提供的信息,解答下列问题:
(1)设装运A种物资的车辆数为x,装运B种物资的车辆数为y.求y与x的函数关系式;
(2)如果装运A种物资的车辆数不少于5辆,装运B种物资的车辆数不少于4辆,那么车辆的安排有几种方案?并写出每种安排方案;
(3)在(2)的条件下,若要求总运费最少,应采用哪种安排方案?请求出最少总运费.
|
物资种类 |
A |
B |
C |
|
每辆汽车运载量(吨) |
12 |
10 |
8 |
|
每吨所需运费(元/吨) |
240 |
320 |
200 |
考点:一次函数的应用;一元一次不等式组的应用。
专题:函数思想。
分析:(1)根据题意列式:12x+10y+8(20﹣x﹣y)=200,变形后即可得到y=20﹣2x;
(2)根据装运每种物资的车辆数都不少于5辆,x≥5,20﹣2x≥4,解不等式组即可;
(3)根据题意列出利润与x之间的函数关系可发现是二次函数,利用二次函数的顶点公式即可求得最大值,根据实际意义可知整数x=8时,利润最大.
解答:(7分)解:(1)根据题意,得:12x+10y+8(20﹣x﹣y)=200,12x+10y+160﹣8x﹣8y=2002x+y=20,
∴y=20﹣2x,
(2)根据题意,得: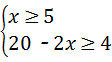 解之得:5≤x≤8
解之得:5≤x≤8
∵x取正整数,∴x=5,6,7,8,
∴共有4种方案,即
|
|
A |
B |
C |
|
方案一 |
5 |
10 |
5 |
|
方案二 |
6 |
8 |
6 |
|
方案三 |
7 |
6 |
7 |
|
方案四 |
8 |
4 |
8 |
(3)设总运费为M元,
则M=12×240x+10×320(20﹣2x)+8×200(20﹣x+2x﹣20)
即:M=﹣1920x+64000
∵M是x的一次函数,且M随x增大而减小,
∴当x=8时,M最小,最少为48640元.
点评:此题考查的是一次函数的应用,主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义求解.注意要根据自变量的实际范围确定函数的最值.
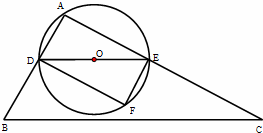
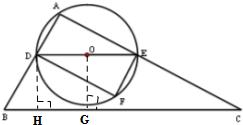
21、(2011•达州)如图,在△ABC中,∠A=90°,∠B=60°,AB=3,点D从点A以每秒1个单位长度的速度向点B运动(点D不与B重合),过点D作DE∥BC交AC于点E.以DE为直径作⊙O,并在⊙O内作内接矩形ADFE,设点D的运动时间为t秒.
(1)用含t的代数式表示△DEF的面积S;
(2)当t为何值时,⊙O与直线BC相切?
考点:切线的性质;矩形的性质;解直角三角形。
专题:综合题。
分析:(1)用t将AD和AE表示出来,利用三角形的面积计算方法列出关于t的函数关系式即可;
(2)过点O作OG⊥BC于G,过点D作DH⊥BC于H,在△DBH中利用解直角三角形的知识表示出DH和OG,利用相切的定义求得t的值即可.
解答:解:(1)∵DE∥BC,
∴∠ADE=∠B=60°,
在△ADE中,
∵∠A=90°,
∴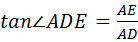 ,
,
∵AD=1×t=t,
∴AE=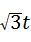 ,
,
又∵四边形ADFE是矩形,
∴S△DEF=S△ADE=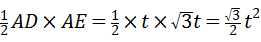 (0≤t<3),
(0≤t<3),
∴S=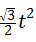 (0≤t<3);
(0≤t<3);
(2)过点O作OG⊥BC于G,过点D作DH⊥BC于H,
∵DE∥BC,
∴OG=DH,
∠DHB=90°,
在△DBH中,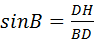 ,
,
∵∠B=60°,BD=AB﹣AD,AD=t,AB=3,
∴DH=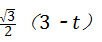 ,
,
∴OG=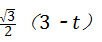 ,
,
当OG=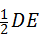 时,⊙O与BC相切,
时,⊙O与BC相切,
在△ADE中,
∵∠A=90°,∠ADE=60°,
∴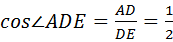 ,
,
∵AD=t,
∴DE=2AD=2t,
∴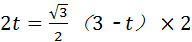 ,
,
∴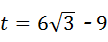 ,
,
∴当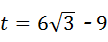 时,⊙O与直线BC相切.
时,⊙O与直线BC相切.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
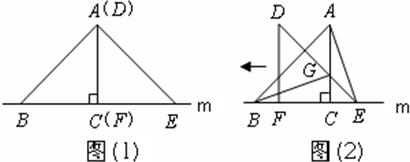
20、(2011•达州)如图,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△DEF的边FE也在直线m上,边DF与边AC重合,且DF=EF.
(1)在图(1)中,请你通过观察、思考,猜想并写出AB与AE所满足的数量关系和位置关系;(不要求证明)
(2)将△DEF沿直线m向左平移到图(2)的位置时,DE交AC于点G,连接AE,BG.猜想△BCG与△ACE能否通过旋转重合?请证明你的猜想.
考点:旋转的性质;全等三角形的判定与性质;等腰直角三角形。
专题:作图题。
分析:(1)根据题意,BC=AC=DF=EF,且AC⊥BC,可知△ABC,△DEF为等腰直角三角形,得出结论;
(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合.已知BC=AC,由(1)可知∠DEF=45°,可知△CEG为等腰直角三角形,则CG=CE,利用“SAS”证明△BCG≌△ACE,得出结论.
解答:解:(1)AB=AE,AB⊥AE;
(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合(或将△ACE绕点C逆时针旋转90°后能与△BCG重合),
理由如下:
∵AC⊥BC,DF⊥EF,B、F、C、E共线,
∴∠ACB=∠ACE=∠DFE=90°,
又∵AC=BC,DF=EF,
∴∠DFE=∠D=45°,
在△CEG中,∵∠ACE=90°,
∴∠CGE=∠DEF=90°,
∴CG=CE,
在△BCG和△ACE中,
∵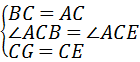 ,
,
∴△BCG≌△ACE(SAS),
∴将△BCG绕点C顺时针旋转90°后能与△ACE重合(或将△ACE绕点C逆时针旋转90°后能与△BCG重合).
点评:本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定与性质.关键是熟练运用等腰直角三角形的性质解题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com