
题目列表(包括答案和解析)
190. P是△ABC所在平面外一点,PA、PB、PC两两垂直,G为△PAB的重心,E、F分别是BC、PB 上的点,且BE∶EC=PF∶FB=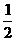 ,求证:平面GEF⊥平面PBC
,求证:平面GEF⊥平面PBC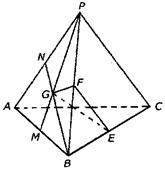
解析:∵G为△PAB的重心,∴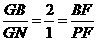 ∴GF∥PA.
∴GF∥PA.
∵PA⊥PB PA⊥PC,∴PA⊥面PBC.∴GF⊥面PBC,∴面GFE⊥面PBC.
189. 在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC和SC于D和E,又 SA=AB,SB=BC.求以BD为棱,以BDE与BDC为面的二面角度数.
∵E为SC的中点 ∴BE⊥SC ∴SC⊥面BDE SC⊥BD 面SA⊥BD ∴BD⊥面SAC 即BD⊥AC BD⊥DE ∴∠EDC为所求.
设SA=a则AB=a SB=BC=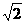 a SC=2a
∠ASC=60° ∠SCA=30° ∠EDC=60°
a SC=2a
∠ASC=60° ∠SCA=30° ∠EDC=60°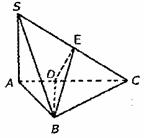
2.过点O作平行于DG的直线,则为所求。
1.作DG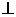 直线PF,则可得AC
直线PF,则可得AC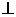 平面PDB,所以EF
平面PDB,所以EF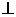 平面PDB
平面PDB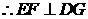
 DG
DG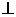 平面PEF。DG为D点到平面PEF的距离
平面PEF。DG为D点到平面PEF的距离
188. (如图)已知正方形ABCD的边长为1,过D作PD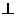 平面ABCD,且PD=1,E、F分别是AB和CD的中点。(1)求D点到平面PEF的距离;(2)求直线AC到平面PEF的距离。
平面ABCD,且PD=1,E、F分别是AB和CD的中点。(1)求D点到平面PEF的距离;(2)求直线AC到平面PEF的距离。
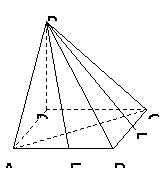
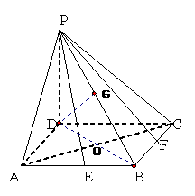
解析: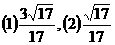
187.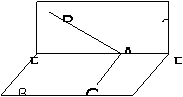 如图,A是直二面角
如图,A是直二面角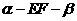 的棱EF上的点,AB、CD分别是
的棱EF上的点,AB、CD分别是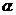 、
、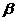 内的射线,
内的射线,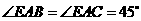 ,求
,求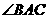 的大小.
的大小.
解析:
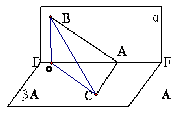 作BO
作BO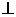 DF,可得BO
DF,可得BO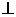 平面
平面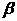 ,解三角形ABC,根据余弦定理可得。
,解三角形ABC,根据余弦定理可得。
186.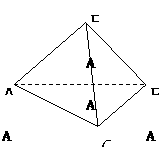 如图,
如图,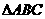 是等腰直角三角形,AC=BC=a,P是
是等腰直角三角形,AC=BC=a,P是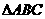 所在平面外一点,PA=PB=PC=
所在平面外一点,PA=PB=PC=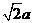 。(1)求证:平面
。(1)求证:平面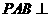 平面ABC;(2)求PC与
平面ABC;(2)求PC与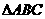 所在平面所成的角。
所在平面所成的角。
解析:
(1)取AB的中点O,连PO,证明PO⊥面ABC,(2)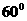
185. P是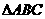 所在平面外一点,若
所在平面外一点,若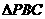 和
和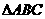 都是边长为2的正三角形,PA=
都是边长为2的正三角形,PA=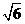 ,求二面角P-BC-A的大小。
,求二面角P-BC-A的大小。
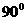 解析:取BC的中点D,连结PD、AD,易证∠PDA为二面角的平面角
解析:取BC的中点D,连结PD、AD,易证∠PDA为二面角的平面角
184. 在正方体ABCD-A1B1C1D1中,E为CC1中点,F为AC和BD的交点.
求证:A1F⊥平面BED.
解析:∵AA1⊥面ABCD,AF是A1F在ABCD上的射影,由AC⊥BD
得A1F⊥BD,取BC的中点G,连FG,B1G,由AB⊥BC1,∴FG⊥面BC1,
∴B1G是A1F在面BC1上的射影,又B1G⊥BE,∴BE⊥A1F,∴A1F⊥面BED;
183. 已知直线a∥直线b,a⊥平面α,求证b⊥α.
解析:过a与α的交点作两相交直线m、n,由a⊥α,则a⊥m,a⊥n,又b∥a,∴b⊥m,b⊥n,
∴b⊥α
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com