
题目列表(包括答案和解析)
202. 正四面体棱长为a,求其内切球与外接球的表面积。
解析:设正四面体的面BCD和面ACD的中心分别为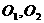 ,连结
,连结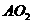 与
与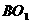 并延长,必交于CD的中点E,又
并延长,必交于CD的中点E,又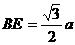 ,
,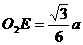 ,连接
,连接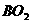 ,在Rt△
,在Rt△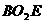 中,
中,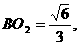 连结
连结 与
与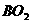 交于
交于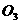 ,由Rt△
,由Rt△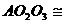 Rt△
Rt△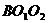 ,∴
,∴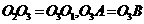 ,同理可证
,同理可证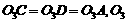 到另二面的距离也等
到另二面的距离也等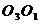 ,
,
∴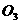 为四面体外接球与内接球的球心,由△
为四面体外接球与内接球的球心,由△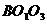 ∽△
∽△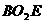 ,∴
,∴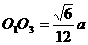 ,
,
∴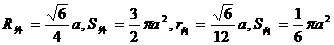
201. .已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半,且AB=BC=AC=2,求球的体积。
解析:过A、B、C三点截面的小圆的半径就是正△ABC的外接圆的半径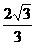 ,
,
它是Rt△中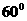 所对的边,其斜边为
所对的边,其斜边为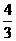 ,即球的半径为
,即球的半径为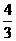 ,∴
,∴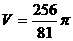 ;
;
220.
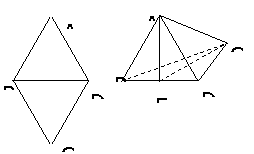
如图,将锐角A为60°,边长为a的菱形ABCD沿BD折成60°的二面角,则A与C之间的距离为___________。
解析: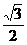 a
a
219. 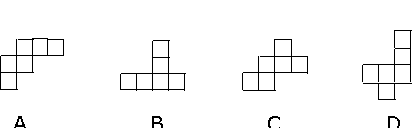 下列四个平面图形中,每个小四边形皆为正方形,其中可以沿两个正方形的相邻边折叠围成一个立方体的图形是
( )
解析:C
下列四个平面图形中,每个小四边形皆为正方形,其中可以沿两个正方形的相邻边折叠围成一个立方体的图形是
( )
解析:C
218.已知平面α⊥平面β,平面α⊥平面γ,且β∩γ=a,求证:a⊥α。
解析: 此题需要作出辅助线,可有多种证明方法。
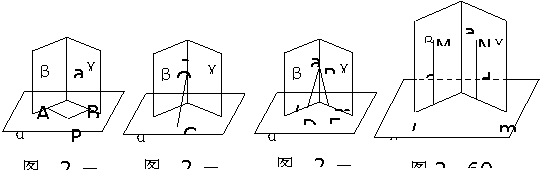
证法1:如图2-57:在α内取一点P,作PA⊥β于A,PB⊥γ于B,
则PA⊥a,PB⊥a,又PA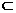 α,PB
α,PB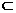 α,PA∩PB=P,∴ a⊥α。
证法2:如图2-58,在a上任取一点Q,作QC ⊥α于C,∵β∩γ=a,∴Q∈β,
又β⊥α,∴QC
α,PA∩PB=P,∴ a⊥α。
证法2:如图2-58,在a上任取一点Q,作QC ⊥α于C,∵β∩γ=a,∴Q∈β,
又β⊥α,∴QC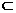 β,同理可证QC
β,同理可证QC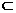 γ,∴QC为β与γ的交线a,∴ a⊥α。
证法3:如图2-59,在a上取点R,在β内作RD垂直于α、β的交线l于D,
γ,∴QC为β与γ的交线a,∴ a⊥α。
证法3:如图2-59,在a上取点R,在β内作RD垂直于α、β的交线l于D,
∴RD⊥α,同法在γ内,作RE垂直于α,交α与γ的交线m于E,则RE⊥α,过平面外一点,作这个平面的垂线是惟一的,∴RD、RE重合,则它既包含于β,又包含于γ,
∴ a⊥α。 证法4:如图2-60,在β、γ内分别取M、N分别作α、β的交线l和α、γ的交线m的垂线c,d,则c⊥α,d⊥α,c//d,c//a,∴ a⊥α。
点评: 此题是线线,线面,面面垂直转化典型题,多解题,对沟通知识和方法,开拓解题思路是有益的。
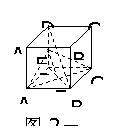
217. 判定下列命题的真假 (1)两个平面垂直,过其中一个平面内一点作与它们的交线垂直的直线,必垂直于另一个平面;
(2)两个平面垂直,分别在这两个平面内且互相垂直的两直线,一定分别与另一平面垂直; (3)两平面垂直,分别在这两个平面内的两直线互相垂直。
解析:(1)若该点在两个平面的交线上,则命题是错误的,
如图2-55,正方体AC1中,平面AC⊥平面AD1,平面AC∩平面AD1=AD,
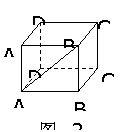 在AD上取点A,连结AB1,则AB1⊥AD,即过棱上一点A的直线AB1
与棱垂直,但AB1与平面ABCD不垂直,其错误的原因是AB1没有保证在平面ADD1A1内,可以看出:线在面内这一条件的重要性;
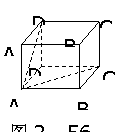
(2)该命题注意了直线在平面内,但不能保证这两条直线都与棱垂直,如图2-56,在正方体AC1中,平面AD1⊥平面AC,AD1
在AD上取点A,连结AB1,则AB1⊥AD,即过棱上一点A的直线AB1
与棱垂直,但AB1与平面ABCD不垂直,其错误的原因是AB1没有保证在平面ADD1A1内,可以看出:线在面内这一条件的重要性;
(2)该命题注意了直线在平面内,但不能保证这两条直线都与棱垂直,如图2-56,在正方体AC1中,平面AD1⊥平面AC,AD1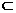 平面ADD1A1,AB
平面ADD1A1,AB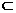 平面ABCD,且AB⊥AD1,即AB与AD1相互垂直,但AD1与平面ABCD不垂直;
(3)如图2-56:正方体AC1中,平面ADD1A1⊥平面ABCD,AD1
平面ABCD,且AB⊥AD1,即AB与AD1相互垂直,但AD1与平面ABCD不垂直;
(3)如图2-56:正方体AC1中,平面ADD1A1⊥平面ABCD,AD1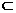 平面ADD1A1,AC
平面ADD1A1,AC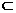 平面ABCD,AD1与AC所成的角为60,即AD1与AC不垂直
平面ABCD,AD1与AC所成的角为60,即AD1与AC不垂直
 解:由上面的分析知,命题⑴、⑵、⑶都是假命题。
解:由上面的分析知,命题⑴、⑵、⑶都是假命题。
点评:在利用两个平面垂直的性质定理时,要注意下列的三个条件缺一不可:①两个平面垂直;②直线必须在其中一个面内;③直线必须垂直它们的交线。
216.在正方体木块ABCD-A1B1C1D1的表面上有一动点P由顶点A出发按下列规则向点C1移动; ⑴点P只能沿着正方体木块的棱或表面对角线移动; ⑵点P每一变化位置,都使P点到C1点的距离缩短。 动点P共有_________种不同的运行路线。 解析:通过画图逐一计数,共得12种不同路线(从B到C1,就有3种不同路线)
经过一条边,一条对角线的情况有6种,
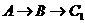 ,
,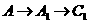 ,
,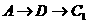
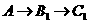 ,
,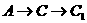 ,
,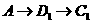
经过三条边的情况有6种:
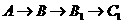 ,
,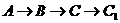 ,
,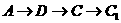
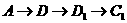 ,
,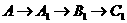 ,
,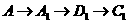
215. 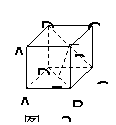 如图2-22:在长方体AC1中,
(1)求证:BC1//平行平面AB1D1
(2)若E、F分别是D1C,BD的中点,则EF//ADD1A1
解析:(1)∵D1C1
如图2-22:在长方体AC1中,
(1)求证:BC1//平行平面AB1D1
(2)若E、F分别是D1C,BD的中点,则EF//ADD1A1
解析:(1)∵D1C1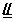 DC
DC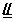 AB
∴ABC1D1是平行四边形
BC1//AD1
又BC1
AB
∴ABC1D1是平行四边形
BC1//AD1
又BC1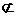 平面AB1D1,又AD1
平面AB1D1,又AD1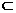 平面AB1D1
平面AB1D1
BC1//平面AB1D1
(2)证明:连结AF、CF、AD1,
∵ABCD是正方形,且F是BD的中点,知A、F、C三点共线,
且F是AC的中点,又E是CD1的中点
∴EF//AD,又EF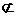 平面ADD1A1,AD
平面ADD1A1,AD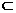 平面ADD1A1,
∴EF//平面ADD1A1
平面ADD1A1,
∴EF//平面ADD1A1
214. 直线a//直线b,直线a与平面α相交,判定直线b与平面α的位置关系,并证明你的结论
证明:假设直线b与α不相交,则b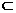 α或b//α
(1)若b
α或b//α
(1)若b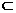 α,由a//b,b
α,由a//b,b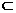 α,a
α,a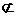 α
α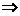 a//α,与a与平面α相交矛盾,故b
a//α,与a与平面α相交矛盾,故b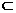 α不可能。
(2)若b//α,又a// b,a,b可以确定平面β,设α∩β=c,由c
α不可能。
(2)若b//α,又a// b,a,b可以确定平面β,设α∩β=c,由c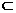 α,知b与c没有公共点,又b、c同在平面β内,故b//c,又a//b,故a//c,c
α,知b与c没有公共点,又b、c同在平面β内,故b//c,又a//b,故a//c,c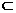 α,a
α,a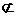 α
α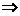 a//α,这与a与平面α相交矛盾。故b不平行α。
综上所述,b与α必相交。
a//α,这与a与平面α相交矛盾。故b不平行α。
综上所述,b与α必相交。
212.如图2-20,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN//平面BCE。
解析: 要证MN//平面BCE,就是要在平面BCE上找一条直线,证明它与MN平行即可。
证明: 连结AN并延长,交BE延长张于G,连结CG。
由AF//BG,知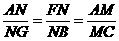 ,故MN//CG,MN
,故MN//CG,MN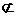 平面BCE,CG
平面BCE,CG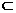 平面BCE,于是MN//平面BCE。
平面BCE,于是MN//平面BCE。
 点评:证线面平行,通常转化为证线线平行,关键是在平面内找到所需的线。
213. 如图2-21,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,
(1)判断BD1和过A、C、E三点的平面的位置关系,
并证明你的结论。
(2)求
点评:证线面平行,通常转化为证线线平行,关键是在平面内找到所需的线。
213. 如图2-21,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,
(1)判断BD1和过A、C、E三点的平面的位置关系,
并证明你的结论。
(2)求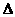 ACE的面积。
证明(1):连结BD,令BD∩AC=F。
∵BD1和过A、C、E三点的平面平行,
则F是DB的中点,又E是DD1的中点,
∴EF∥BD1
又EF
ACE的面积。
证明(1):连结BD,令BD∩AC=F。
∵BD1和过A、C、E三点的平面平行,
则F是DB的中点,又E是DD1的中点,
∴EF∥BD1
又EF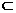 平面ACE,BD1
平面ACE,BD1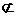 平面ACE,
∴BD1∥平面ACE
(2)在正方形ABCD中,AB=2,AC=2
平面ACE,
∴BD1∥平面ACE
(2)在正方形ABCD中,AB=2,AC=2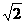 ,∴AF=
,∴AF=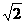 在直角△ADE中,AD=2,DE=1,∴AE=
在直角△ADE中,AD=2,DE=1,∴AE=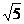
在Rt△EAF中,EF=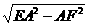 =
=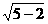 =
=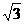 ∴
∴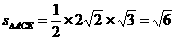
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com