
题目列表(包括答案和解析)
248. 已知:A1、B1、C1和A2、B2、C2分别是两条异面直线l1和l2上的任意三点,M、N、R、T分别是A1A2、B1A2、B1B2、C1C2的中点.求证:M、N、R、T四点共面.
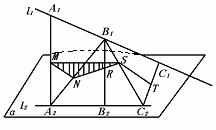
证明 如图,连结MN、NR,则MN∥l1,NR∥l2,且M、N、R不在同一直线上(否则,根据三线平行公理,知l1∥l2与条件矛盾).∴
MN、NR可确定平面β,连结B1C2,取其中点S.连RS、ST,则RS∥l2,又RN∥l2,∴ N、R、S三点共线.即有S∈β,又ST∥l1,MN∥l1,∴MN∥ST,又S∈β,∴
ST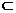 β.
β.
∴ M、N、R、T四点共面.  =2:1
=2:1
又 是正三角形
是正三角形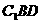 的BD边上的高和中线,∴点G是正三角形
的BD边上的高和中线,∴点G是正三角形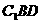 的中心.故
的中心.故 ,即
,即 。
。
证明二:由(I)知,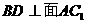 ,
,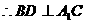 ,
,
当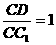 时,平行六面体的六个面是全等的菱形.同
时,平行六面体的六个面是全等的菱形.同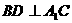 的证法可得
的证法可得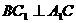 , 又
, 又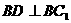 ,所以
,所以 。
。
247.设 相交于G.,
相交于G., ,且
,且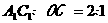 ,所以
,所以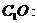 如图,已知正方体ABCD-A1B1C1D1的棱长为a,求异面直线A1C1与BD1的距离.
如图,已知正方体ABCD-A1B1C1D1的棱长为a,求异面直线A1C1与BD1的距离.

解析:本题的关键是画出A1C1与BD1的公垂线,连B1D1交A1C1于O,在平面BB1D1内作OM⊥BD1,则OM就是A1C1与BD1的公垂线,问题得到解决.
解 连B1D1交A1C1于O,作OM⊥BD1于M.
∴ A1C1⊥B1D1,BB1⊥A1C1,BB1∩B1D1=B1.
∴ A1C1⊥平面BB1D1. ∴ A1C1⊥OM,又OM⊥BD1.
∴ OM是异面直线A1C1与BD1的公垂线.
在直角ΔBB1D1中作B1N⊥BD1于N.
∵
BB1·B1D1=B1N·BD1,a· a=B1N·
a=B1N· a,
a,
∴
B1N=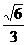 a,OM=
a,OM=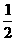 B1N=
B1N=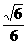 a.
a.
故异面直线A1C1与BD1的距离为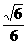 a.
a.
评析:作异面直线的公垂线一般是比较困难的,只有熟练地掌握线、线垂直,线、面垂直的关系后才能根据题目所给条件灵活作出.本题在求OM的长度时,主要运用中位线和面积的等量关系.
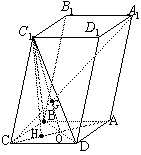
246.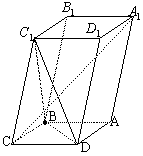 如图,已知平行六面体
如图,已知平行六面体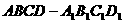 的底面ABCD是菱形,且
的底面ABCD是菱形,且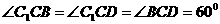 ,(1)证明:
,(1)证明: 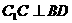 ;
;
(II)假定CD=2,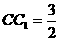 ,记面
,记面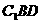 为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
(III)当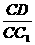 的值为多少时,能使
的值为多少时,能使 ?请给出证明. 解析:(I)证明:连结
?请给出证明. 解析:(I)证明:连结 、AC,AC和BD交于.,连结
、AC,AC和BD交于.,连结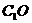 , ∵四边形ABCD是菱形,∴AC⊥BD,BC=CD,
, ∵四边形ABCD是菱形,∴AC⊥BD,BC=CD, 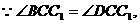 可证
可证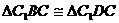 ,
,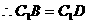 ,
,
故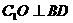 ,但AC⊥BD,所以
,但AC⊥BD,所以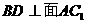 ,从而
,从而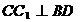 ;
;
(II)解:由(I)知AC⊥BD,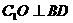 ,
,
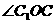 是二面角α-BD-β的平面角,在
是二面角α-BD-β的平面角,在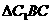 中,BC=2,
中,BC=2,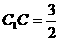 ,
,
 ,
,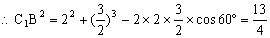 ∵∠OCB=60°,
∵∠OCB=60°,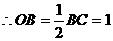 ,
,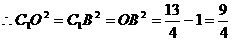 ,故C1O=
,故C1O=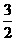 ,即C1O=C1C,作
,即C1O=C1C,作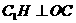 ,垂足为H,∴点H是.C的中点,且
,垂足为H,∴点H是.C的中点,且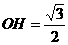 ,所以
,所以 ;
;
(III)当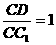 时,能使
时,能使
证明一:∵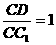 ,所以
,所以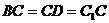 ,又
,又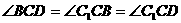 ,由此可得
,由此可得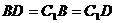 ,∴三棱锥
,∴三棱锥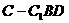 是正三棱锥.,
是正三棱锥.,
245.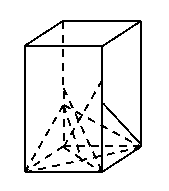 已知正四棱柱ABCD-A1B1C1D1中,点P是DD1的中点,且截面EAC与底面ABCD成450角,AA1=2a,AB=a,(1)设Q是BB1上一点,且BQ
已知正四棱柱ABCD-A1B1C1D1中,点P是DD1的中点,且截面EAC与底面ABCD成450角,AA1=2a,AB=a,(1)设Q是BB1上一点,且BQ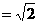 a,求证:DQ
a,求证:DQ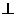 面EAC;(2)判断BP与面EAC是否平行,并说明理由?(3)若点M在侧面BB1C1C及其边界上运动,并且总保持AM
面EAC;(2)判断BP与面EAC是否平行,并说明理由?(3)若点M在侧面BB1C1C及其边界上运动,并且总保持AM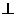 BP,试确定动点M所在的位置。
BP,试确定动点M所在的位置。
解析:(1)证:首先易证AC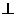 DQ,再证EO
DQ,再证EO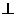 DQ(O为AC与BD的交点)在矩形BDD1B1中,可证
DQ(O为AC与BD的交点)在矩形BDD1B1中,可证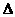 EDO与
EDO与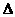 BDQ都是直角三角形,由此易证EO
BDQ都是直角三角形,由此易证EO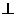 DQ,故DQ
DQ,故DQ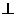 面EAC得证;
面EAC得证;
(2)若BP与面EAC平行,则可得BP//EO,在三角形BPD中,O是BD中点,则E也应是PD中点,但PD=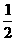 DD1=a,而ED=DO=
DD1=a,而ED=DO=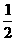 BD=
BD=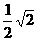 a,故E不是PD中点,因此BP与面EAC不平行;
a,故E不是PD中点,因此BP与面EAC不平行;
(3)易知,BP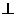 AC,要使AM
AC,要使AM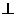 BP,则M一定在与BP垂直的平面上,取BB1中点N,易证BP
BP,则M一定在与BP垂直的平面上,取BB1中点N,易证BP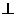 面NAC,故M应在线段NC上。
面NAC,故M应在线段NC上。
244.如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直。点M在AC上移动,点N在BF上移动,若CM=x ,BN=y, 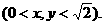 (1)求MN的长(用x,y表示);(2)求MN长的最小值,该最小值是否是异面直线AC,BF之间的距离。
(1)求MN的长(用x,y表示);(2)求MN长的最小值,该最小值是否是异面直线AC,BF之间的距离。
解析:在面ABCD中作MP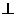 AB于P,连PN,则MP
AB于P,连PN,则MP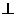 面ABEF,所以MP
面ABEF,所以MP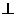 PN,PB=1-AP=
PN,PB=1-AP=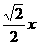 在
在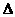 PBN中,由余弦定理得:PN2=
PBN中,由余弦定理得:PN2=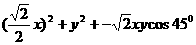
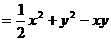 ,在
,在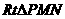 中,MN=
中,MN=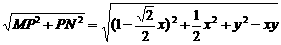
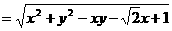
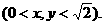 ;
;
(2)MN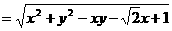
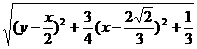 ,故当
,故当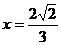 ,
,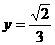 时,MN有最小值
时,MN有最小值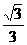 。且该最小值是异面直线AC,BF之间的距离。
。且该最小值是异面直线AC,BF之间的距离。
243. 如图,边长均为a的正方形ABCD、ABEF所在的平面所成的角为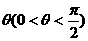 。点M在AC上,点N在BF上,若AM=FN ,(1)求证:MN//面BCE ; (2)求证:MN
。点M在AC上,点N在BF上,若AM=FN ,(1)求证:MN//面BCE ; (2)求证:MN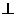 AB;
AB;
(3)求MN的最小值.
解析:(1)如图,作MG//AB交BC于G, NH//AB交BE于H, MP//BC交AB于P, 连PN, GH , 易证MG//NH,且MG=NH, 故MGNH为平行四边形,所以MN//GH , 故MN//面BCE ;
(2)易证AB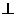 面MNP, 故MN
面MNP, 故MN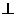 AB ;
AB ;
(3)
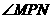 即为面ABCD与ABEF所成二面角的平面角,即
即为面ABCD与ABEF所成二面角的平面角,即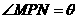 ,设AP=x , 则BP=a-x , NP=a-x , 所以:
,设AP=x , 则BP=a-x , NP=a-x , 所以: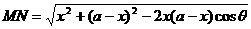
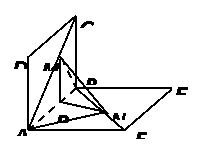
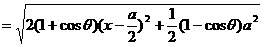 ,
,
故当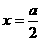 时,MN有最小值
时,MN有最小值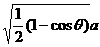 .
.
242.如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直。点M在AC上移动,点N在BF上移动,若CM=BN=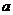
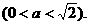 (1)求MN的长;
(1)求MN的长;
(2)当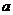 为何值时,MN的长最小; (3)当MN长最小时,求面MNA与面MNB所成的二面角
为何值时,MN的长最小; (3)当MN长最小时,求面MNA与面MNB所成的二面角 的大小。
的大小。
解析:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连接PQ,依题意可得MP∥NQ,且MP=NQ,即MNQP是平行四边形。∴MN=PQ,由已知,CM=BN=a,CB=AB=BE=1,
∴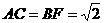 ,
,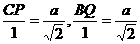 , 即
, 即
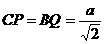 ,
,
∴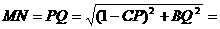
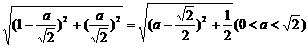
(2)由(1)知: 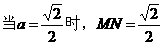 ,
,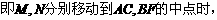
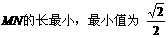
(3)取MN的中点G,连接AG、BG,∵AM=AN,BM=BN,∴AG⊥MN,BG⊥MN,
∴∠AGB即为二面角α的平面角。又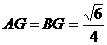 ,所以由余弦定理有
,所以由余弦定理有
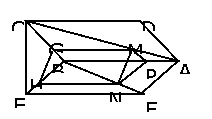
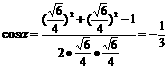 。故所求二面角
。故所求二面角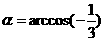 。
。
241. 已知点P是正方形ABCD所在的平面外一点,PD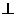 面AC,PD=AD=
面AC,PD=AD=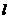 ,设点C到面PAB的距离为d1,点B到平面PAC的距离为d2,则( )
,设点C到面PAB的距离为d1,点B到平面PAC的距离为d2,则( )
(A)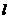 <d1 <d2(B)d1<
d2<
<d1 <d2(B)d1<
d2<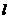 (C)d1<
(C)d1<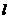 < d2(D)d2<d1<
< d2(D)d2<d1<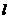
 解析:
解析: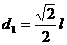 ,
,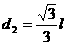 ,故d2<d1<
,故d2<d1<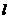 ,选D。
,选D。
40. 如图,P是正角形ABC所在平面外一点,M、N分别是AB和PC的中点,且PA=PB=PC=AB=a。
(1)求证:MN是AB和PC的公垂线
(2)求异面二直线AB和PC之间的距离
解析:(1)连结AN,BN,∵△APC与△BPC是全等的正三角形,又N是PC的中点
∴AN=BN
又∵M是AB的中点,∴MN⊥AB
同理可证MN⊥PC
又∵MN∩AB=M,MN∩PC=N
∴MN是AB和PC的公垂线。
(2)在等腰在角形ANB中,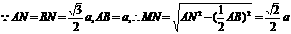
即异面二直线AB和PC之间的距离为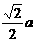 .
.
38. 在空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,EF=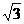 ,求AD与BC所成角的大小
,求AD与BC所成角的大小
(本题考查中位线法求异面二直线所成角)
解析:取BD中点M,连结EM、MF,则

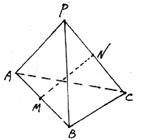
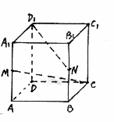 39. 如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱AA1和BB1的中点,求异面直线CM与D1N所成角的正弦值.(14分)
39. 如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱AA1和BB1的中点,求异面直线CM与D1N所成角的正弦值.(14分)
(本题考查平移法,补形法等求异面二直线所成角)
解析:取DD1中点G,连结BG,MG,MB,GC得矩形MBCG,记MC∩BG=0
则BG和MC所成的角为异面直线CM与D1N所成的角.
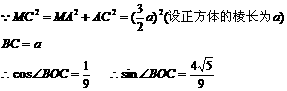
 而CM与D1N所成角的正弦值为
而CM与D1N所成角的正弦值为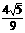
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com