
题目列表(包括答案和解析)
2. (昆明一中二次月考理) 从4名男生和3名女生中选出4人参加迎新座谈会,若这4人中必须既有男生又有女生,不同的选法共有( )
A.140种 B. 120种 C.35种 D.34种
答案:D
1.(2009玉溪一中期末)设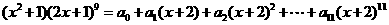 ,
,
则 的值为( )
的值为( )
A.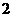 B.
B. C.
C. D.
D.

答案 C
解析:令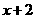 =1,右边为
=1,右边为 ;左边把
;左边把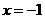 代入
代入
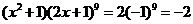 ,
,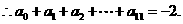 选C.
选C.
排列、组合和二项式定理
2010年联考题
50.(2006上海春)电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,则共有 种不同的播放方式(结果用数值表示).
解:分二步:首尾必须播放公益广告的有A22种;中间4个为不同的商业广告有A44种,从而应当填 A22·A44=48. 从而应填48.
49.(2006天津)用数字0,1,2,3,4组成没有重复数字的五位数,则其中数字1,2相邻的偶数有 个(用数字作答).
解析:可以分情况讨论:① 若末位数字为0,则1,2,为一组,且可以交换位置,3,4,各为1个数字,共可以组成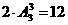 个五位数;②
若末位数字为2,则1与它相邻,其余3个数字排列,且0不是首位数字,则有
个五位数;②
若末位数字为2,则1与它相邻,其余3个数字排列,且0不是首位数字,则有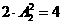 个五位数;③
若末位数字为4,则1,2,为一组,且可以交换位置,3,0,各为1个数字,且0不是首位数字,则有
个五位数;③
若末位数字为4,则1,2,为一组,且可以交换位置,3,0,各为1个数字,且0不是首位数字,则有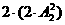 =8个五位数,所以全部合理的五位数共有24个。
=8个五位数,所以全部合理的五位数共有24个。
48.(2006陕西)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,则不同的选派方案共有 种 .
解析:可以分情况讨论,① 甲去,则乙不去,有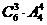 =480种选法;②甲不去,乙去,有
=480种选法;②甲不去,乙去,有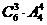 =480种选法;③甲、乙都不去,有
=480种选法;③甲、乙都不去,有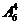 =360种选法;共有1320种不同的选派方案
=360种选法;共有1320种不同的选派方案
47.(2006陕西)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有 种
解析:某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,可以分情况讨论,①
甲、丙同去,则乙不去,有 =240种选法;②甲、丙同不去,乙去,有
=240种选法;②甲、丙同不去,乙去,有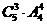 =240种选法;③甲、乙、丙都不去,有
=240种选法;③甲、乙、丙都不去,有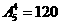 种选法,共有600种不同的选派方案.
种选法,共有600种不同的选派方案.
46.(2006全国I)安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有__________种。(用数字作答)解析:先安排甲、乙两人在后5天值班,有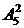 =20种排法,其余5人再进行排列,有
=20种排法,其余5人再进行排列,有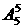 =120种排法,所以共有20×120=2400种安排方法。
=120种排法,所以共有20×120=2400种安排方法。
45.(2006辽宁)5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_______种.(以数作答)
[解析]两老一新时, 有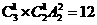 种排法;
种排法;
两新一老时, 有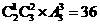 种排法,即共有48种排法.
种排法,即共有48种排法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com