
题目列表(包括答案和解析)
2. (2010江西理)10.过正方体
(2010江西理)10.过正方体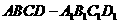 的顶点A作直线L,使L与棱
的顶点A作直线L,使L与棱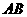 ,
,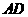 ,
,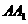 所成的角都相等,这样的直线L可以作
所成的角都相等,这样的直线L可以作
A.1条 B.2条 C.3条 D.4条
[答案]D
[解析]考查空间感和线线夹角的计算和判断,重点考查学生分类、划归转化的能力。第一类:通过点A位于三条棱之间的直线有一条体对角线AC1,第二类:在图形外部和每条棱的外角和另2条棱夹角相等,有3条,合计4条。
1.(2010浙江理)(6)设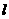 ,
, 是两条不同的直线,
是两条不同的直线,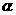 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是
(A)若 ,
,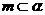 ,则
,则 (B)若
(B)若 ,
, ,则
,则
(C)若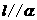 ,
,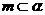 ,则
,则 (D)若
(D)若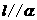 ,
, ,则
,则
[答案] B
解析:选B,可对选项进行逐个检查。本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理,也蕴含了对定理公理综合运用能力的考察,属中档题
2010年高考题
9.(2010全国卷2理)(22)(本小题满分12分)
设函数 .
.
(Ⅰ)证明:当 时,
时,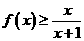 ;
;
(Ⅱ)设当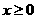 时,
时, ,求a的取值范围.
,求a的取值范围.
[命题意图]本题主要考查导数的应用和利用导数证明不等式,考查考生综合运用知识的能力及分类讨论的思想,考查考生的计算能力及分析问题、解决问题的能力.
8.(2010浙江理) (22)(本题满分14分)已知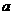 是给定的实常数,设函数
是给定的实常数,设函数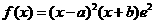 ,
,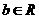 ,
,
 是
是 的一个极大值点.
的一个极大值点.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)设 是
是 的3个极值点,问是否存在实数
的3个极值点,问是否存在实数 ,可找到
,可找到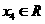 ,使得
,使得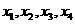 的某种排列
的某种排列 (其中
(其中 =
= )依次成等差数列?若存在,求所有的
)依次成等差数列?若存在,求所有的 及相应的
及相应的 ;若不存在,说明理由.
;若不存在,说明理由.
解析:本题主要考查函数极值的概念、导数运算法则、导数应用及等差数列等基础知识,同时考查推理论证能力、分类讨论等综合解题能力和创新意识。
(Ⅰ)解:f’(x)=ex(x-a) 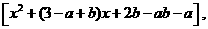
令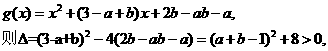
于是,假设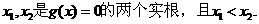
(1) 当x1=a 或x2=a时,则x=a不是f(x)的极值点,此时不合题意。
(2) 当x1 a且x2
a且x2 a时,由于x=a是f(x)的极大值点,故x1<a<x2.
a时,由于x=a是f(x)的极大值点,故x1<a<x2.
即
即
所以b<-a
所以b的取值范围是(-∞,-a)

此时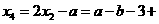
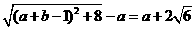
或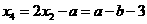

(2)当 时,则
时,则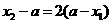 或
或

于是
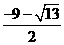


此时
综上所述,存在b满足题意,
当b=-a-3时,
 时,
时,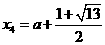
 时,
时,
7.(2010湖南文)21.(本小题满分13分)
已知函数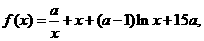 其中a<0,且a≠-1.
其中a<0,且a≠-1.
(Ⅰ)讨论函数 的单调性;
的单调性;
(Ⅱ)设函数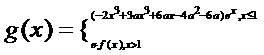 (e是自然数的底数)。是否存在a,使
(e是自然数的底数)。是否存在a,使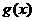 在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。



6.(2010江苏卷)14、将边长为1m正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记 ,则S的最小值是________。
,则S的最小值是________。
[解析] 考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小正三角形的边长为 ,则:
,则:
(方法一)利用导数求函数最小值。
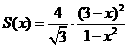 ,
,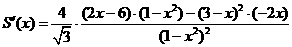

 ,
,
当 时,
时, 递减;当
递减;当 时,
时, 递增;
递增;
故当 时,S的最小值是
时,S的最小值是 。
。
(方法二)利用函数的方法求最小值。
令 ,则:
,则:
故当 时,S的最小值是
时,S的最小值是 。
。
5.(2010江西理) 12.如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为
12.如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为 ,则导函数
,则导函数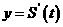 的图像大致为
的图像大致为

[答案]A
[解析]本题考查函数图像、导数图、导数的实际意义等知识,重点考查的是对数学的探究能力和应用能力。最初零时刻和最后终点时刻没有变化,导数取零,排除C;总面积一直保持增加,没有负的改变量,排除B;考察A、D的差异在于两肩位置的改变是否平滑,考虑到导数的意义,判断此时面积改变为突变,产生中断,选择A。
4.(2010全国卷2文)(7)若曲线 在点
在点 处的切线方程是
处的切线方程是 ,则
,则
(A)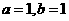 (B)
(B) 
(C)  (D)
(D)
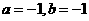
[解析]A:本题考查了导数的几何意思即求曲线上一点处的切线方程
∵  ,∴
,∴
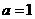 ,
, 在切线
在切线 ,∴
,∴

3.(2010辽宁理)(1O)已知点P在曲线y=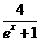 上,a为曲线在点P处的切线的倾斜角,则a的取值范围是
上,a为曲线在点P处的切线的倾斜角,则a的取值范围是
(A)[0,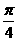 ) (B)
) (B)
 (D)
(D) 
[答案]D
[命题立意]本题考查了导数的几何意义,求导运算以及三角函数的知识。
[解析]因为 ,即tan a≥-1,所以
,即tan a≥-1,所以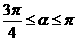
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com