
题目列表(包括答案和解析)
2.(本小题满分13分)
已知数列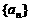 中,
中,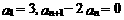 ,数列
,数列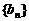 中,
中,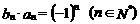 .
.
(Ⅰ)求数列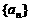 通项公式;
通项公式;
(Ⅱ)求数列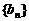 通项公式以及前
通项公式以及前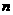 项的和.
项的和.
1.(本小题满分13分)
在 中,内角
中,内角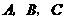 对边的边长分别是
对边的边长分别是 ,已知
,已知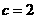 ,
,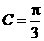 .
.
(Ⅰ)若 的面积等于
的面积等于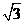 ,求
,求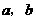 ;
;
(Ⅱ)若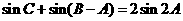 ,求
,求 的面积.
的面积.
3、画原图形
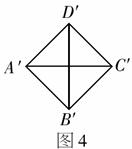 例3 如图4,
例3 如图4,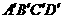 是边长为1的正方形,又知它是某
是边长为1的正方形,又知它是某
个四边形按斜二测画法画出的直观图,请画出该四边形的原图形.
解:由于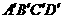 是边长为1的正方形,则
是边长为1的正方形,则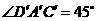 .
.
于是取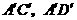 所在的直线分别为
所在的直线分别为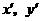 轴.
轴.
画两条垂直的有向直线,分别为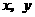 轴,
轴, 为原点,
为原点,
 在
在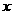 轴上,且
轴上,且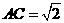 ,再在
,再在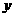 轴上取点
轴上取点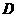 ,使
,使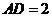 ,取
,取 的中点
的中点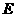 ,连结
,连结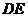 并延长至
并延长至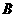 使
使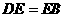 ,连结
,连结 得四边形
得四边形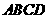 ,即为正方形
,即为正方形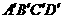 的原图形,见图5.
的原图形,见图5.
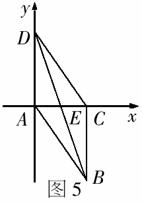 至此,可以看出斜二测画法看似是一种比较简单的画图方法,但当我们认真深入其中时,会发现并非都是简单问题.逆向斜二测问题有时还真有点难度,必须细心分析,才能保证万无一失.
至此,可以看出斜二测画法看似是一种比较简单的画图方法,但当我们认真深入其中时,会发现并非都是简单问题.逆向斜二测问题有时还真有点难度,必须细心分析,才能保证万无一失.
2、求面积
例2 一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图3则原平面图形的面积为( )
A.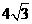 B.
B.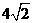 C.
C.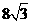 D.
D.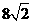
解:由斜二测画法可知,原图形是一个平行四边形,且平行四边形的一组对边长为2,在斜二测图形中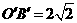 ,且
,且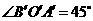 ,那么在原图形中,
,那么在原图形中, 且
且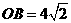 ,因此,原平面图形的面积为
,因此,原平面图形的面积为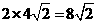 ,故正确答案为(D).
,故正确答案为(D).
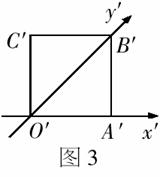 评析:本题抓住在斜二测画法中平行于
评析:本题抓住在斜二测画法中平行于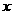 轴的线段画为平行于
轴的线段画为平行于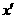 轴,
轴,
得到了原图形是平行四边形;画结合原图形中垂直在直观图中画为夹
角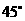 ,得到原图形中的高,从而得到结论.
,得到原图形中的高,从而得到结论.
4.利用函数单调性知识解(证)数列中的单调性问题
例4 已知函数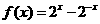 ,数列
,数列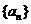 满足
满足 .
.
(1)求数列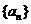 的通项公式;
的通项公式;
(2)求证数列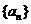 是递减数列.
是递减数列.
分析:①本题已知函数关系式,并给出了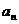 的关系式,将其看作关于
的关系式,将其看作关于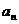 的方程解出即可.②数列是特殊的函数,借助函数的增减性的方法来证明数列的增减性.
的方程解出即可.②数列是特殊的函数,借助函数的增减性的方法来证明数列的增减性.
(1)解:∵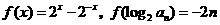 ,,
,,
∴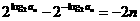 ,即
,即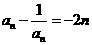 ..
..
∴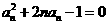 , (※)
, (※)
解得 
又∵ ,∴
,∴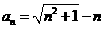 ;
;
(2)证明:由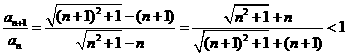 .
.
又∵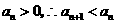 ..
..
∴数列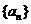 是递减数列.
是递减数列.
评注:本题主要应用函数与方程的思想解题,(※)式可看成是关于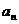 的方程;而求出的通项公式又反映了
的方程;而求出的通项公式又反映了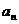 是关于n的函数.解题过程中
是关于n的函数.解题过程中 这个细节要注意.
这个细节要注意.
3.等差数列的前n项和可看成是关于n的二次函数
例3 已知等差数列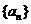 ,首项
,首项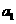 ,且
,且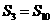 ,问此数列前几项的和最大?最大值是多少?
,问此数列前几项的和最大?最大值是多少?
分析:等差数列前n项和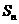 为特殊的二次函数,所以可采用配方法求其最值.
为特殊的二次函数,所以可采用配方法求其最值.
解:设等差数列公差为d,前n项和为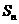 ,
,
∵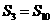 ,即
,即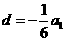 ,
,
∴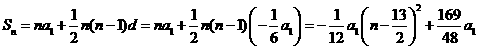 ,
,
∴当n=6或n=7时,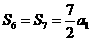 为最大.
为最大.
评注:关于等差数列前n项和最大(小)问题,可转化为二次函数问题,再结合二次函数的最值问题加以分析,但应特别注意,当对称轴不是正自然数时,应将与对称轴最接近的两个自然数代入函数关系式,再求值比较,以便确定n取何值时,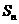 最大(最小).
最大(最小).
2.构造一次函数模型,利用一次函数图象性质解题
例2 等差数列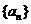 的前n项和为30,前2n项和为100,则它的前3n项和为( ).
的前n项和为30,前2n项和为100,则它的前3n项和为( ).
(A)30 (B)170 (C)210 (D)260
分析:运用等差数列求和公式,先对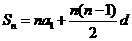 进行变形,
进行变形,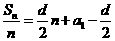 ,则
,则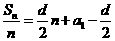 可以看成是关于n的一次函数,再利用点共线的性质求解.
可以看成是关于n的一次函数,再利用点共线的性质求解.
解:由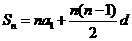 ,可得
,可得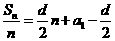 ,
,
由此可知数列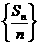 成等差数列,
成等差数列,
∴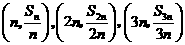 三点共线.
三点共线.
∴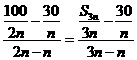 ,
,
∴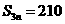 .
.
评注:①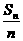 可以看成是关于n的一次函数,其图象是直线上的离散点,本题是利用点共线的条件建立方程求解
可以看成是关于n的一次函数,其图象是直线上的离散点,本题是利用点共线的条件建立方程求解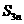 的.运用该法还可以推得在等差数列中若
的.运用该法还可以推得在等差数列中若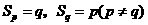 ,则
,则 .②等差数列的通项公式
.②等差数列的通项公式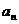 也可以看成是关于n的一次函数,利用该性质可推知等差数列中若
也可以看成是关于n的一次函数,利用该性质可推知等差数列中若 ,则
,则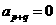 .
.
1.等差数列的通项公式可以看成自变量为n的一次函数(公差d≠0时)
例1已知等差数列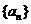 ,其前n项和为
,其前n项和为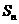 ,是否存在常数k,使得
,是否存在常数k,使得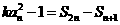 成立.
成立.
分析:将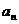 看成是n的一次函数,设出函数解析式并代入进行求解.
看成是n的一次函数,设出函数解析式并代入进行求解.
解:设存在常数k,使得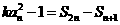 成立,
成立,
令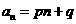 (p、q为常数),
(p、q为常数),
则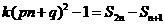 .①
.①
又∵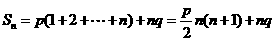 ,,
,,
代入①式变为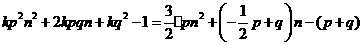 ,
,
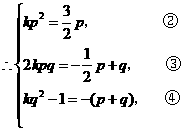
由②,得 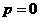 或
或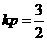 .
.
将p=0代入③、④不成立.
将kp=代入③,得 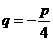 ,
,
代入④,得 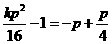 ,即
,即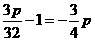 ,
,
∴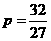 ,从而得出
,从而得出 .
.
∴存在常数k,使得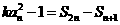 成立.
成立.
评注:存在型探索性问题,是指判断在某些确定条件下的某一数学对象(数值、图形、函数等)不确定的问题.这类问题常常出现“是否存在”、“是否有”等形式的疑问句,以示结论有待于确定.解答此类问题的思路是:通常假设题中的数学对象存在(或结论成立)或暂且认可其中一部分的结论,然后在这个前提下进行逻辑推理,若由此导出矛盾,则否定假设;否则,给出肯定结论的证明.
3.综合利用平均数和标准差来估计总体
例3 公交车的数量太多容易造成资源的浪费,太少又难以满足乘客的需求.为此,公交公司在某站台随机调查了80名乘客,他们的候车时间如下所示(单位:分):
17 14 20 12 10 24 18 17 1 22 13 19 28 5 34 7
25 18 28 1 15 31 12 11 10 16 12 9 10 13 19 10
12 12 16 22 17 23 16 15 16 11 9 3 13 2 18 22
19 9 23 28 15 21 28 12 11 14 15 3 11 6 2 18
25 5 12 15 20 16 12 28 20 12 28 15 8 32 18 9
(1)这80名乘客候车时间的平均数是多少?标准差呢?
(2)你能为公交公司提出什么建议?
解:(1)这80名乘客候车时间的平均数约为15.5,标准差约为7.5;
(2)公交公司可以适当增加公交车的数量.
规律总结:根据问题合理选取样本是统计决策的一个基本前提,在这个前提下,我们可以从所抽取的样本中提取数据信息,如平均数、标准差这些基本的数字特征,然后用这些数字特征对实际生活提供科学的指导与建议.
2.用样本方差和标准差估计总体
详释:方差和标准差是描述一个样本和总体的波动大小的特征数.总体方差和标准差较难求得,通常我们是用样本方差和标准差去估计相应总体方差和标准差.
例2 甲、乙两篮球运动员在本赛季前八场比赛中,每场的投篮得分如下:
甲 15,18,20,12,22,25,28,20
乙 26,15,21,14,17,23,19,25
若你是一个篮球队的主教练,请你对甲、乙两名运动员作一下比较,看哪一位运动员的发挥更稳定.
解:利用方差来比较两运动员投篮得分的稳定性.
 ,
,
由于 ,所以乙运动员每场投篮水平的发挥更具稳定性.
,所以乙运动员每场投篮水平的发挥更具稳定性.
规律总结:平均数代表了总体的平均水平,而标准差反映了总体的稳定程度,我们可用平均数与标准差从不同的方面估计总体.如下面这道例题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com