
题目列表(包括答案和解析)
对一求定义域问题主要掌握三大限制:①分式的分母不为零;②偶次方根的被开方数不小于零;③对数的真数为正,底数大于零且不为1.
例1 (2005年全国高考江苏卷)函数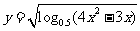 的定义域为
.
的定义域为
.
解:由题意知, ,即
,即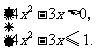
从而可得函数的定义域为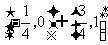 .
.
3.方程思想
通过观察、分析、判断将问题化归为方程的问题,利用方程的性质,实现问题与方程的互相转化,达到解决问题的目的.
例3 过已知点 的直线
的直线 与圆
与圆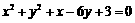 相交于
相交于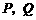 两点,且
两点,且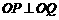 (其中
(其中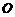 为原点),求直线
为原点),求直线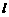 的方程.
的方程.
分析:因为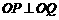 ,若设
,若设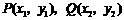 ,则
,则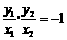 ,由
,由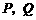 在圆及直线上,可借助方程求解.
在圆及直线上,可借助方程求解.
解:设直线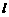 的方程为
的方程为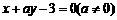 ,
,
则点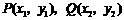 的坐标满足方程组
的坐标满足方程组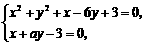
消去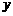 ,得
,得 ,
,
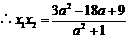 . ①
. ①
由方程组消去 ,得
,得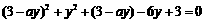 ,
,
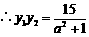 . ②
. ②
依题意知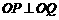 ,
, ,即
,即 .
.
由①,②知,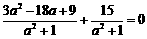 ,
,
整理,得 ,解得
,解得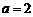 或
或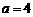 .
.
 所求直线
所求直线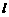 的方程为
的方程为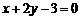 或
或 .
.
评注:本题巧用根与系数的关系,列出 ,进而求得方程.
,进而求得方程.
2.转化思想
所谓转化思想,就是在研究和解决有关数学问题时,采用某种手段将问题通过变换使之转化,进而得到解决问题的一种方法.一般地,总是将复杂的问题转化为简单的问题,将难解决的问题通过变换转化为容易解决的问题,将未解决的问题通过变换转化为已解决的问题.
例2 求圆 上的点到直线
上的点到直线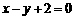 的最小、最大距离.
的最小、最大距离.
分析:由于圆是一个对称图形,依其对称性,圆上的点到直线的最小(大)距离为圆心到直线的距离减去(加上)半径.
解:由圆的方程 易知圆心坐标为
易知圆心坐标为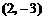 ,半径
,半径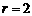 .
.
而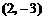 到直线
到直线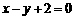 的距离为
的距离为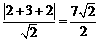 .
.
故圆上的点到直线的最大距离为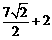 ,最小距离为
,最小距离为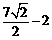 .
.
评注:凡是涉及与圆有关的距离问题,均可转化为圆心到直线的距离问题.
1.数形结合思想
例1 已知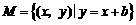 ,
,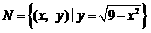 ,若
,若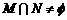 ,求
,求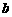 的取值范围.
的取值范围.
分析:由于本题所给圆不是整圆,而仅是圆的一部分,所以应用数形结合处理.
解:集合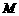 是斜率为1,在
是斜率为1,在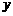 轴上截距为
轴上截距为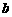 的一束平行线,集合
的一束平行线,集合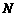 是以原点为圆心,半径为3的圆在
是以原点为圆心,半径为3的圆在 轴上方的部分(包括与
轴上方的部分(包括与 轴的交点).
轴的交点).

由题意作出图形,如上图,当直线 过
过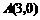 时,
时,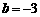 .
.
当直线与半圆相切时,由点到直线的距离公式得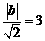 .
.
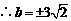 ,由图形易知
,由图形易知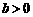 ,故
,故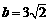 .
.
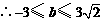 .
.
评注:在涉及到半圆或圆的一部分的题目时,应用数形结合处理较简单.
4.求参数范围问题
例4 在平面直角坐标系中,若方程 表示的曲线为椭圆,则
表示的曲线为椭圆,则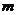 的取值范围为( ).
的取值范围为( ).
A.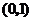 B.
B.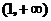 C.
C.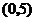 D.
D.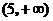
解:已知等式可变形为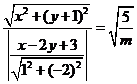 ,此式可看成点
,此式可看成点 到定点
到定点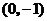 的距离与到直线
的距离与到直线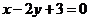 的距离之比为常数
的距离之比为常数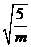 ,由统一定义知
,由统一定义知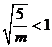 ,所以
,所以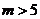 ,故答案为D.
,故答案为D.
3.求轨迹方程
例3 点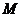 与点
与点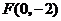 的距离比它到直线
的距离比它到直线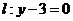 的距离小1,求点
的距离小1,求点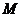 的轨迹方程.
的轨迹方程.
解:由题意可知,点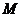 与点
与点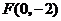 的距离和它到直线
的距离和它到直线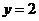 的距离相等,根据定义知,轨迹是抛物线.因此
的距离相等,根据定义知,轨迹是抛物线.因此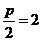 ,∴
,∴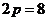 ,故点M的轨迹方程是
,故点M的轨迹方程是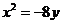 .
.
2.求最值问题
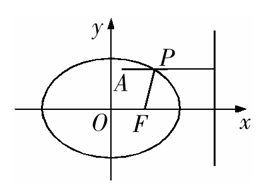 例2 已知椭圆方程为
例2 已知椭圆方程为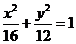 ,右焦点为
,右焦点为 ,
,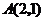 为其内部一点,
为其内部一点, 为椭圆上一动点,求
为椭圆上一动点,求 点坐标,使
点坐标,使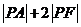 最小.
最小.
解:如图,由题意得
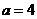 ,
,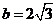 ,
,
∴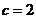 ,
,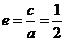 ,
,
由统一定义知 即为
即为 到右准线的距离,
到右准线的距离,
因此,要使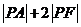 最小,
最小, 点除了应在
点除了应在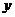 轴的右侧外,还要使
轴的右侧外,还要使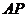 与过
与过 点且与准线垂直的线共线即可,
点且与准线垂直的线共线即可,
由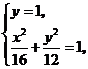 ,解得
,解得 点坐标为
点坐标为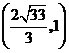 .
.
1.求距离问题
例1 椭圆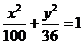 上一点
上一点 到左焦点的距离为6,则点
到左焦点的距离为6,则点 到右准线的距离是多少?
到右准线的距离是多少?
解:由第一定义,点 到右焦点的距离为
到右焦点的距离为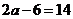 ,
,
再由统一定义,得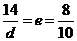 ,
,
∴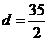 ,所以点
,所以点 到右准线的距离为
到右准线的距离为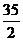 .
.
椭圆、双曲线和抛物线统称为圆锥曲线,在解题过程中,我们经常用到它们的统一定义:平面内与一个定点 和一条定直线
和一条定直线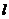 的距离之比为常数
的距离之比为常数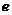 的点的轨迹,当
的点的轨迹,当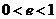 时,轨迹是椭圆;当
时,轨迹是椭圆;当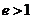 时,轨迹是双曲线;当
时,轨迹是双曲线;当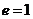 时,轨迹是抛物线.其中,点
时,轨迹是抛物线.其中,点 是曲线的焦点,直线
是曲线的焦点,直线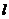 是对应于焦点
是对应于焦点 的曲线的准线,
的曲线的准线,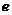 为离心率.
为离心率.
圆锥曲线的统一定义把焦点、准线和离心率巧妙地联系起来,在解相关的题目时,如能巧妙运用统一定义,能起到化繁为简的作用,使问题简洁明快的得以解决.
3.“放回”与“不放回”
例3 从含有两件正品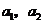 和一件次品
和一件次品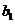 的三件产品中每次任取一件,连续取两次.
的三件产品中每次任取一件,连续取两次.
(1)若每次取出后不放回,求取出的两件产品中恰有一件次品的概率;
(2)若每次取出后放回,求取出的两件产品中恰有一件次品的概率.
解:(1)每次取一件,取后不放回地连续取两次,其一切可能的结果为: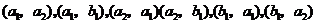 ,其中小括号中左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产品.用A表示“取出的两件中,恰好有一件次品”这一事件,则事件
,其中小括号中左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产品.用A表示“取出的两件中,恰好有一件次品”这一事件,则事件 由
由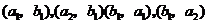 这4个事件组成,因而
这4个事件组成,因而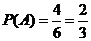 ;
;
(2)有放回地取出两件,其一切可能的结果为:
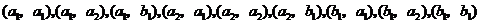 ,用
,用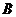 表示“恰有一件次品”这一事件,则事件
表示“恰有一件次品”这一事件,则事件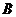 由
由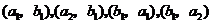 这4个事件组成,因而
这4个事件组成,因而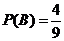 .
.
注:对于“互斥”与“对立”这两个易混概念的理解,既是重点又是难点,我们特在第四版《一定要抓住“互斥”与“对立”》一文中进行详细的讲解分析,大家可以参考学习.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com