5、已知n为正整数, 且 n²－71能被7n+55整除, 试求n 的值.

4、试找出由0，1，2，3，4，5，6这7个数字组成的没有重复数字的七位数中，能被165整除的最大数和最小数(要求写出推理过程)。

3、设a,b,c,d是四个整数, 且使得m = (ab +cd)²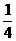－(a²+b²－c²－d²)是个非零整数, 求证: | m |一定是个合数.

2、在黑板上写出下面的数2，3，4……，2001。甲先去擦其中的一个数，然后乙再擦去一个数和，如此轮流下去，若最后剩下的两个数互质，则甲胜；若最后剩下的两个数不互质，则乙胜，你如果想胜，应当选甲还是选乙？说明理由(注：两数互质是两个数无1以外的公约数，如2与5互质，3与15不互质)。

1、某商场向顾客发放9999张购物券，每张购物券上印有一个四位数的号码，从0001到9999号，如果号码的前两位数字之和等于后两位数字之和，则称这张购物券为“幸运券”。例如号码0734，因0+7=3+4，所以这个号码的购物券是幸运券，证明：这个商场所发的购物券中，所有幸运券的号码之和能被101整除。

10、数100！的各位数字从右面向左看时(即从个位数、十位数、……看过去)，第一个不是0的数字是　　　　　　　　　 。

初中数学夏令营赛前专题训练(一)

数论(A)

9、设ABCDEF为正六边形，一只青蛙开始在顶点A处，它每次可随意地跳到相邻两顶点之一，若在5次之内跳到D点，则停止跳动，若5次之内不能到达D点，则跳完5次也停止跳动，那么这只青蛙从开始到停止，可能出现的不同跳法共　　　

种。

8、已知tgα=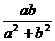,其中a、b为常数，且a²+b²≠0，则(a²+b²)sinαcosα－abcos²α的值为　　　　　　　　　 。

7、函数y=ax²+bx+c的图象是开口向下的抛物线，a、b、c各不相等，且都在集合A={| n |≤5，n∈Z}中取值，则这些抛物线中通过点(0，－1)的有　　　 条。

6、凸四边形ABCD中，∠ABC=60°,∠BAD=∠BCD=90°，

AB=2，CD=1，对角线AC、BD交于点O，如图，则sin∠AOB

=　　　　　 。