1.4的平方根是_____________.

　　 求参数的取值范围是一类重要问题，解题关键是建立关于这个参数的不等式组，必须

将已知的所有条件加以转化。

　　 例6.已知函数f(x)=(x2-ax+3a)在区间[2，+∞)上是减函数，则实数a的取值范

围是_______。

　　 分析如下：

　 令u=x2-ax+3a，y=u。

　 因为y=u在(0，+∞)上是减函数

　 ∴ f(x)=(x2-ax+3a)在[2，+∞)上是减函数?

 ?u=x2-ax+3a在[2，+∞)上是增函数，且对任意x∈[2，+∞)，都有u＞0。

对称轴x=在2的左侧或过(2，0)点，且u(2)＞0。　 ?

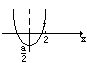
　 ?-4＜a≤4

　 　例7.若f(x)=loga(3-ax)在[0，1]上是减函数，则a的取值范围是_______。

　 令u=-ax+3＞0，y=logau，由于a作对数的底数，所以a＞0且a≠1，由u=-ax+3＞0得x＜。

在[0，1]上，且u是减函数。

　　 ∴ f(x)=loga(3-ax)在[0，1]上是减函数。

 ? y=logau是增函数，且[0，1](-∞，]

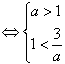
 ? 　? 1＜a＜3 

　所以a的取值范围是(1，3)。

　 习题

　1.函数y=在区间[4，5]上的最大值是_______，

最小值是_______。

 2.函数y=(2-x-x2)的单调减区间是_______。

　 答案： 

1.；1。

 2.(-2，- )。

　 定理：设y=f(u)，u=g(x)，已知u=g(x)在[a，b]上是单调增(减)函数，y=f(u)在区

间[g(a)，g(b)](或[g(b)，g(a)]上是单调增(减)函数，那么复合函数y=f[g(x)]在[a，b]

上一定是单调函数，并有以下结论：

　 判断复合函数的单调性的步骤如下：(1)求复合函数定义域；(2)将复合函数分解为若干

个常见函数(一次、二次、幂、指、对函数)；(3)判断每个常见函数的单调性；(4)将中间

变量的取值范围转化为自变量的取值范围；(5)求出复合函数的单调性。

　 例4.讨论函数y=0.8x2-4x+3的单调性。

　 解：函数定义域为R。

　 令u=x2-4x+3，y=0.8u。

　 指数函数y=0.8u在(-∞，+∞)上是减函数，

　 u=x2-4x+3在(-∞，2]上是减函数，在[2，+∞)上是增函数，

　 ∴ 函数y=0.8x2-4x+3在(-∞，2]上是增函数，在[2，+∞)上是减函数。

　 这里没有第四步，因为中间变量允许的取值范围是R，无需转化为自变量的取值范围。

　　 例5.讨论函数y=(log2x)2+log2x的单调性。

　　 解：显然函数定义域为(0，+∞)。

　　 令 u=log2x，y=u2+u

　　 ∵ u=log2x在(0，+∞)上是增函数，

　　 y=u2+u在(-∞，- ]上是减函数，在[- ，+∞)上是增函数(注意(-∞，-]及

[-，+∞)是u的取值范围)

因为u≤- log2x≤- 0＜x≤，(u≥- log2x≥- x≥)

　 所以y=(log2x)2+log2x在(0，]上是减函数，在[，+∞)上是增函数。

　　 函数y=log2x是对数函数，那么函数y=log2(2x-1)是什么函数呢?我们可以这样理解：

设y=log2u，u=2x-1，因此函数y=log2(2x-1)是由对数函数y=log2u和一次函数u=2x-1经

过复合而成的。

　　 一般地，如果y是u的函数，而u又是x的函数，即y=f(u)，u=g(x)，那么y关于x的函

数y=f[g(x)]叫做函数f和g的复合函数，u叫做中间变量。

　　 例1.已知f(x)=x+，g(x)=x2-2，求f[g(x)]和g[f(x)]的解析式。

　　 解：f[g(x)]=f(x2-2)=(x2-2)+；

　　　　 g[f(x)]=g(x+)=(x+)2-2=x2+。

　　 例2.已知f(x)的定义域为[0，4]，求函数f(x2)的定义域。

　　 解：f(x2)可以看作ψ(x)=f[g(x)]，其中u=g(x)=x2，则f(x2)=f(u)，即ψ(x)=f(u)。

　　 由已知f(u)的定义域为[0，4]，即0≤u≤4，所以0≤x2≤4，解得-2≤x≤2。

　　 ∵ 函数f(x2)的定义域为[-2，2]。

　　 例3.求函数y=的值域。

　　 分析：令u=x2-1，y=，函数y=的定义域为x≠±1，分别作出函数u=x2-1，

y=的图象。

　　 由x≠±1→u≥-1，且u≠0，→y＞0，或y≤-1。

　 故函数y=的值域为(-∞，-1]∪(0，+∞)。

19、已知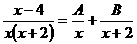，求A，B的值。