1. (87(3)3分)设a，b是满足ab＜0，的实数，那么 A.|a+b|＞|a－b|　　 B.|a+b|＜|a－b|　 C.|a－b|＜||a|－|b||　 D.|a－b|＞|a|+|b|

考试内容：

不等式.不等式的性质.不等式的证明.不等式的解法.含有绝对值的不等式.

考试要求：

(1)掌握不等式的性质及其证明，掌握证明不等式的几种常用方法，掌握两个(或三个)正数的算术平均数不小于它们的几何平均数这一定理，并能运用上述性质、定理和方法解决一些问题.

(2)在熟练掌握一元一次不等式(组)、一元二次不等式的解法的基础上初步掌握其他的一些简单的不等式的解法.

(3)会用不等式|a|－|b|≤|a+b|≤|a|+|b|解一些简单问题.

15、如果∣a∣<1,∣b∣<1,且arcsin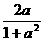+arcsin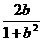=2arctgx ,那么x=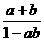

14、设0≤x≤1，求证：cos(arcsinx)<arcsin(cosx)

13、当0≤x≤p 时，比较arcsin(cosx),arcos(sinx)的大小。

12、a,b分别为直角三角形ABC的两条直角边，c是斜边，且arcsin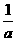+arcsin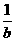=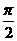，求证：lgc=lga+lgb。

11、已知tg(x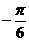)=5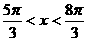，()用反正切函数表示x 。

10、已知sinx=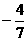，其中x∈[0,2p]，用反正弦函数表示x 。

9、用一个反正弦表示arccos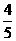+arcsin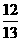

8、求函数y=cos(2arcsinx)+2sin(arcsinx)的最值。