11.3.2 一次函数与一元一次不等式

知识库

4．解析：(1)由图像可知小明到达离家最远的地方需3h，此时，他离家30km．

　　 (2)设直线CD的解析式为y=k₁x+b₁，将C(2，15)，D(3，30)分别代入，

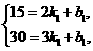　　 得 解得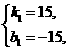

　　 ∴y=15x-15(2≤x≤3)．

　　 当x=2．5时，y=15×2．5-15=22．5(km)．

　　 小明出发2．5h离家22．5km．

　　 (3)设直线EF的解析式为y=k₂x+b₂，将E(4，30)，F(6，0)分别代入，

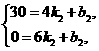　　 得　 解得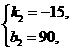

　　 ∴y=-15x+90(4≤x≤6)．

　　 设直线AB的解析式为y=k₃x，将B(1，15)代入，得15=k₃．

　　 ∴y=15x(0≤x≤1)．

　　 将y=12分别代入y=-15x+90，y=15x．

　　 得12=-15x+90，12=15x，

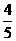　　 ∴x=或x=。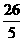

提示：解第(3)题要认真观察、分析，图像应有两种可能．

3．解析：(1)设解析式为y=kx+b，把x₁=2，y₁=30和x₂=6，y₂=10，分别代入，

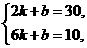　　 得　 解得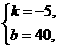　 ∴y=-5x+40．

　　 (2)当y=0时，0=-5x+40，∴x=8．

　　 所以一箱油可供拖拉机工作8h．

2．解析：由已知可得此一次函数与y轴的交点坐标为(0，-2)．

　　 将x=0，y=-2代入y=(m-2)x+m²-6，得-2=m²-6，①

　　 且m的取值应满足m-2≠0．②

　　 由①得m²=4，m=±2，由②得m≠2．

　　 故m=-2．

1．解析：y=10-2x．

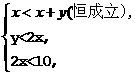
　　 由①得10-2x<2x，-4x<-1，x>．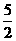

　　 由②得x<5，故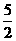<x<5．

　　 提示：注意别漏掉隐含的限制条件2x<10．

2．解析：(1)Q=40-6t．

　　 (2)把Q=10代入Q=40-6t，得10=40-6t，解得t=5．

探究应用拓展性训练

1．解析：(1)y=8+1．80(x-3)=8+1．80x-5．4=1．80x+2．6．

　　 (2)当x=6时，y=1．80×6+2．6=10．8+2．6=13．4<14，因此车费够了．

9．解析：∵点M在直线y=2x+1上，∴当x=-2时，y=-4+1=-3，即k=-3，

　　 ∴M到x轴的距离d=│k│=3．

　　 答案：3

8．解析：直线与x轴、y轴的交点为(-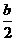，0)，(0，b)

　　 ∴9=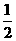×|-|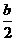×│b│=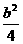，∴b=±6．

7．解析：∵y=-x+a与y=x+b的交点坐标为(m，8)，

∴(m，8)应满足这两个关系式．

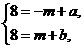
　　 ①+②得a+b=16．

　　 答案：16