6．解析：∵y=kx+b与y=-3x平行，∴k=-3，∴y=-3x+b．

　　 把x=0，y=-2代入，得b=-2，

　　 ∴直线y=kx+b的关系式为y=-3x-2．令y=0，则0=-3x-2，3x=-2，x=-，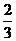

　　 ∴该函数与x轴的交点为(-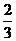，0)

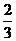　　 答案：(－，0)

　　 提示：要确定函数与坐标轴的交点坐标，首先要求出函数关系式．

5．解析：∵当x₁<x₂时，y₁<y₂，

　　 ∴y的值随x的增大而增大，∴-k>0，即k<0．

　　 答案：k<0

4．解析：∵y=3x+m-1的图像不经过第二象限，∴m-1<0，即m<1．

　　 答案：m<1

3．解析：把y=1代入y=2x-1，得1=2x-1，2x=2，x=1，即m=1．

　　 答案：1

　　 提示：若点在函数的图像上，则点的坐标满足函数的关系式．

∴m>2．答案：m>2.

2．解析：∵y=(m+6)x+(m-2)是一次函数，∴m+6≠0，m≠-6．

　　 答案：m≠-6

8．C　 解析：∵点P(a，b)在第二象限，∴a<0，b>0．

　　 ∴函数y=ax+b的图像不经过第三象限，故应选C．

7．A　 解析：∵y=x-3，∴当y=5时，5=x-3，x=8，即a=8．

　　 当y=3时，3=x-3，x=6，即b=6．

　　 ∴a>b，故应选A．

　　　 提示：本题还可根据函数的增减性分析，对于y=x-3，k=1>0，故y随x的增大而增大，因5>3，故a>b．

6．C　 解析：由图像可看出线段AB是一次函数图像的一段，且经过(0，2)，(3，0)两点，x的取值范围为0≤x≤3．

　　 设函数表达式为y=kx+b，

　　 将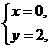 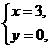　分别代入，

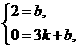　　 得　 解得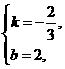

　　 ∴关系式为y=-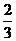x+2(0≤x≤3)．

5．C　 解析：把x=0，y=-1；x=1，y=1分别代入y=kx+b，

　　 得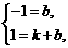　 解得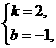

　　 ∴关系式为y=2x-1，故应选C．

4．C　 解析：∵在一次函数y=(1-k)x+k中，k>1，∴1-k<0，

　　 ∴此函数的图解不经过第三象限，故应选C．