
题目列表(包括答案和解析)
4.若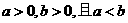 ,则下列式子中成立的是( )
,则下列式子中成立的是( )
 A.
A.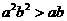 B.
B.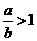 C.
C.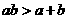 D.
D.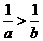
3.下列说法正确的是( )
A.1的平方根是1 B.0的算术平方根是0
C.-1的平方根是-1
D.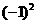 的平方根是-1
的平方根是-1
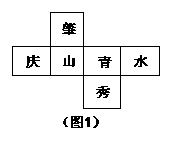
2.如图1是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“青”相对应的面上的汉字是( )
A.庆 B.山 C. 水 D.秀
1. 计算
计算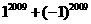 的结果是( )
的结果是( )
A.0 B.2 C. 2 D.4018
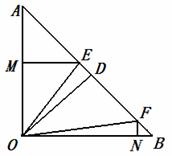
26.解:
(1)证明:∵ 是等腰直角三角形,
是等腰直角三角形,
∴ 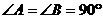
 ∵
∵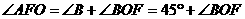
又∵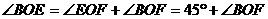
∴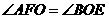
∴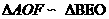 ……………………3分
……………………3分
(2)∵ ∽
∽
∴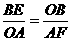
∴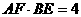 …………………………………6分
…………………………………6分
(3)作斜边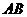 上的高
上的高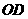 ,并记
,并记
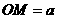 、
、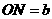 ,则易得
,则易得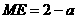 ,
,
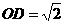 ,
,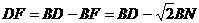
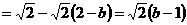 ,
,
由已知条件易得:
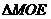 ∽
∽
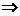
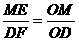
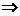
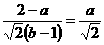
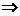
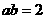 ,
,
即 ;……………………………………………………9分
;……………………………………………………9分
(4)解: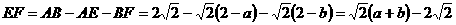
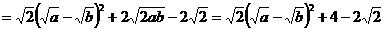 ,
,
所以,当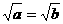 ,
,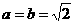 时,
时,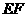 取得最小值
取得最小值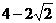 。…………12分
。…………12分
本资料由《七彩教育网》 提供!
25.解:(1) 直线
直线 与
与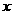 轴相交于点B,
轴相交于点B,
 当
当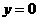 时,
时,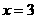 ,
,
 点B的坐标为
点B的坐标为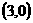 .
.
又 抛物线过
抛物线过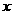 轴上的A,B两点,且对称轴为
轴上的A,B两点,且对称轴为 ,
,
根据抛物线的对称性,
 点
点 的坐标为
的坐标为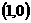 .
.

 过点C,易知C
过点C,易知C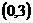 ,
,
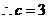 .
.
又 抛物线
抛物线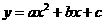 过点
过点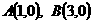 ,
,
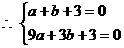
解,得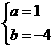
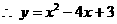 .………………………………………………4分
.………………………………………………4分
(2)连结PB,由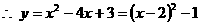 ,得
,得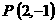 ,
,
设抛物线的对称轴交x轴于点M,在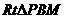 中,
中,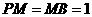 ,
,
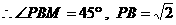 .
.
由点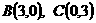 易得
易得 ,在等腰直角三角形
,在等腰直角三角形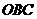 中,
中,
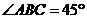 ,
,
由勾股定理,得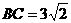 .………………………………………………6分
.………………………………………………6分
假设在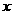 轴上存在点Q,使得以点P,B,Q为顶点的三角形与
轴上存在点Q,使得以点P,B,Q为顶点的三角形与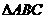 相似.
相似.
①当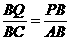 ,
,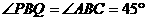 时,
时,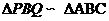 .
.
即错误!不能通过编辑域代码创建对象。,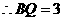 ,
,
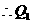 的坐标是
的坐标是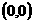 .………………………………………………9分
.………………………………………………9分
②当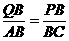 ,
,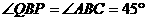 时,
时,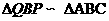 .
.
即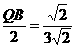 ,
,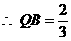 .
.
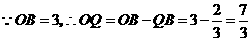 ,
,
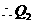 的坐标是
的坐标是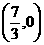 .
.
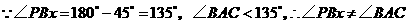 .
.
 点
点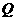 不可能在
不可能在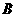 点右侧的
点右侧的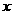 轴上(无此判断,亦不扣分).
轴上(无此判断,亦不扣分).
综上所述,在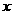 轴上存在两点
轴上存在两点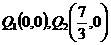 ,能使得以点
,能使得以点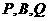 为顶点的三角形与
为顶点的三角形与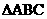 相似.………………………………………………………………12分
相似.………………………………………………………………12分
24.解:(1)∵DQ=t,AP=2t,
∴AQ=3-t,BP=12-2t
∵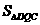 =3t,
=3t, 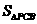 =18-3t,
=18-3t,  =27,
=27,
∴ =9,
=9,
从而证明不论t取何值,四边形QAPC的面积是一个定值,并且这个定值是9;…………3分
(2)不存在……………………………………………………………………………4分
∵∠PCQ=90°
∴由勾股定理知: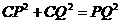 ,
,
∵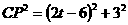 ,
,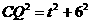 ,
,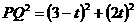 ,
,
∴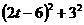 +
+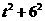
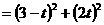 ,
,
∴t=4,
∵0≤t≤3
∴不存在……………………………………………………………………………………6分
(3)分两种情况:
①当∠CPB=90°时,很容易得到AP=6
从而得:2t=6,则t=3………………………………………………………………………8分
②当∠PCB=90°时
由勾股定理知: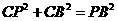
又∵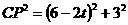 ,
,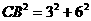 ,
,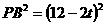 ,
,
∴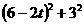 +
+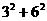
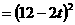
∴t=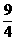
综上所述:当t=3或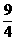 时,△PBC能构成直角三角形。…………………………10分
时,△PBC能构成直角三角形。…………………………10分
23.解:(1)容易证明△BPQ是等边三角形,
∴当四边形BPDQ是平行四边形时,∠BPD=120°…………………4分
(2)分三种情况:
①当∠DPQ是直角时,∠BPD=150°;……………………5分
②当∠PDQ是直角时,∠BPD=105°;……………………6分
③当∠PQD是直角时,∠BPD=105°. …………………7分
(3)也分三种情况:
①当PD=PQ时,∵很容易证明△APB≌△DQB,
∴∠PDQ=∠PQD=40°,∴∠BPD=160°;……………………8分
②当DP=DQ时,同理可求得∠BPD=100°;……………………9分
③当QP=QD时,也同理可得∠BPD=130°. …………………10分
22.解:(1)延长AC到E,使CE=AC,连结EB交CD于点P,则点P就是污水处理厂所在的地方(画出图形)。 ---------------------------------2分
设CP=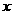 ,则DP=6-
,则DP=6-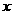
由点A与点E的对称性可知∠APC=∠EPC
又由对顶角相等可知 ∠B PD=∠EPC
∴∠APC=∠BPD
又∵∠ACP=∠BDP=90°
∴△ACP∽△BDP ---------------------4分
∴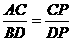
∴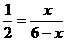 ---------------------5分
---------------------5分
解得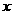 =2
=2
所以,污水厂应建在距离C地2km处。 -------------------------------6分
(2)仿照(1)中建立图形,使AC=1,CD=9,BD=2,设CP=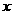 -------7分
-------7分
则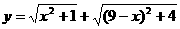 中的
中的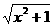 即是图中的AP,
即是图中的AP,
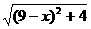 即是图中的DP。
即是图中的DP。
所以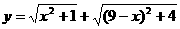 的最小值就是CP+DP的最小值,
的最小值就是CP+DP的最小值,
仿照(1)中找到点A关于直线CD的对称点E,
连结EB,与CD的交点就是所求的点P. -------8分
由△ACP∽△BDP
得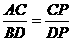
∴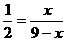
解得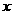 =3
-----------9分
=3
-----------9分
所以当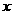 =3时,
=3时,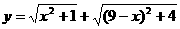 有最小值,最小值是
有最小值,最小值是
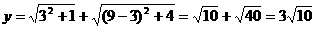 -----10分
-----10分
21.解:(1)当n=1时,直线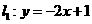 与 x轴和y轴的交点是
与 x轴和y轴的交点是
 (
(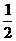 ,0)和
,0)和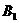 (0,1)
----------------------1分
(0,1)
----------------------1分
所以 =
=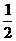 ,
,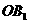 =1,
=1,
∴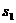 =
=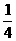 ----------------------------------------3分
----------------------------------------3分
(2) 当n=2时,直线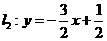 与 x轴和y轴的交点是
与 x轴和y轴的交点是
 (
(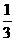 ,0)和
,0)和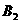 (0,
(0,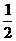 )
)
所以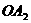 =
=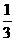 ,
,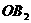 =
=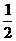 ,
,
∴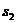 =
=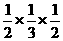 =
=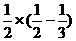 -----------------------4分
-----------------------4分
当n=3时,直线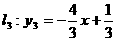 与 x轴和y轴的交点是
与 x轴和y轴的交点是
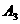 (
(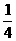 ,0)和
,0)和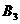 (0,
(0,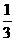 )
)
所以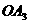 =
=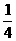 ,
,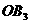 =
=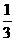 ,
,
∴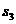 =
=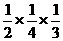 =
=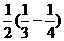 -----------------------5分
-----------------------5分
依次类推,
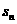 ==
==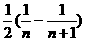 ----------------------------6分
----------------------------6分
∴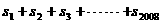 =
=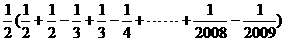 ---7分
---7分
∴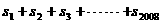 =
=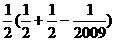
=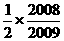
=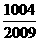 ---------------------8分
---------------------8分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com