
题目列表(包括答案和解析)
9.Rt△ABC中,∠C=90°,AC=8㎝,AB=10㎝,则△ABC的面积为________,最长边上的高等于_______.
8.2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成一个大正方形(如图20所示),如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边是a,较长直角边是b,那么(a+b)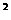 的值为( )
的值为( )
A.13 B.19 C.25 D.169
7.两只小鼹鼠在地下打洞,一只朝前方挖,每分钟挖8cm,另一只
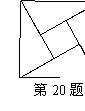 朝左挖,每分钟挖6cm,10分钟之后两只小鼹鼠相距( )
朝左挖,每分钟挖6cm,10分钟之后两只小鼹鼠相距( )
A.50cm B.100cm C.140cm D.80cm
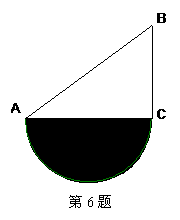
6.如图所示,直角三角形ABC中,∠C=90°,AB=13cm,BC=5cm,则以AC为直径的半圆(阴影部分)的面积为( )
A.18
B.18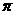 C.36
D.36
C.36
D.36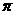
5. 一个圆桶底面直径为10cm,高24cm,则桶内所能容下的最长木
一个圆桶底面直径为10cm,高24cm,则桶内所能容下的最长木
棒为( )
A.20cm B.24cm C.26cm D.30cm
4.下列说法中错误的是( )
A.在△ABC中,若∠A=∠C-∠B,则△ABC是直角三角形;
B.在△ABC中,若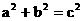 ,则△ABC是直角三角形;
,则△ABC是直角三角形;
C.在△ABC中,若∠A、∠B、∠C的度数比是7:3:4,则△ABC是直角三角形;
D.在△ABC中,若三边长a:b:c=2:2:3,则△ABC是直角三角形.
2.若a、b、c表示△ABC的三边,且满足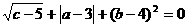 ,则△ABC是( )
,则△ABC是( )
A.等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等边三角形
1.下列各组数是勾股数的为( )
A.2,4,5 B.8,15,17
C.11,13,15 D.4,5,6
20.4 图案的设计与欣赏
第1题. 下列图案中,哪一个可以由图案(1)经过平移得到?( )
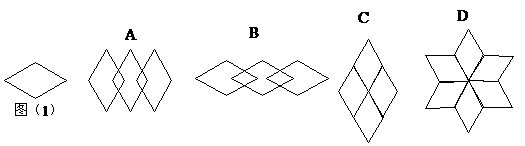
答案:B
第2题. 分析下图的形成过程,它是由哪一个基本图形经过怎样的变换得到的?

答案: 平移
平移
第3题.  图中的4个小正三角形,通过旋转可以与另一个正三角形重合的有( )
图中的4个小正三角形,通过旋转可以与另一个正三角形重合的有( )
A.3对 B.4对 C.5对 D.6对
答案:D
第4题.  先观察①、②、③这3个三角形的变化规律,再按此规律画出第4个图形来.
先观察①、②、③这3个三角形的变化规律,再按此规律画出第4个图形来.
答案:
第5题. 某居民小区为了美化居住环境,决定把一边长为60米的正方形平均分成4份,并在中央留出一块边长是12米的正方形做休息亭,请你设计5种不同的方案,使所分成的4块成旋转对称图形,在它们中种上不同颜色的花卉,并给人以美的享受.
答案:
第6题.
建材市场有正方形地板砖,聂晶晶同学选中了其中的两种,用来铺设新居的客厅,请你帮她设计一种图案,它既成轴对称,又成中心对称,又美观.
答案:
第7题.
建材市场有正方形地板砖,邵雨欣同学选中了其中的三种,请你帮她设计一种图案,用它来铺设客厅,使整个图案既成轴对称,又成中心对称及旋转对称图形,还能给人以美的感受.
答案:
第8题. 你能用圆规作出下图所示的图案吗?
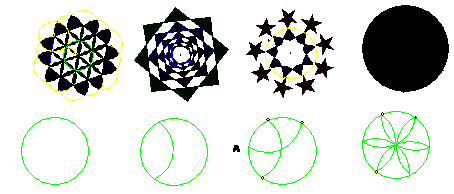
答案:略
第9题.
在下图中作出△ABC平移后的图形,使点B平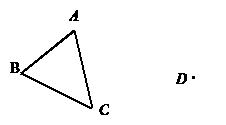 移到点D处,并指出图中对应的线段和对应角.
移到点D处,并指出图中对应的线段和对应角.
答案:略
第10题. 如图,平面直角坐标系中,△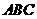 为等边三角形,其中点
为等边三角形,其中点 、
、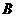 、
、 的坐标分别为
的坐标分别为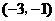 、
、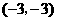 、
、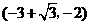 .现以
.现以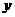 轴为对称轴作△
轴为对称轴作△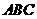 的对称图形,得
的对称图形,得
△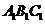 ,再以
,再以 轴为对称轴作△
轴为对称轴作△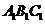 的对称图形,得△
的对称图形,得△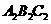 .
.
(1)直接写出点 、
、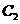 的坐标;
的坐标;
(2)能否通过一次旋转将△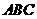 旋转到△
旋转到△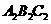 的位置?你若认为能,请作出肯定的回答,并直接写出所旋转的度数;你若认为不能,请作出否定的回答(不必说明理由);
的位置?你若认为能,请作出肯定的回答,并直接写出所旋转的度数;你若认为不能,请作出否定的回答(不必说明理由);
(3)设当△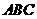 的位置发生变化时,△
的位置发生变化时,△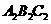 、△
、△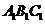 与△
与△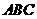 之间的对称关系始终保持不变.
之间的对称关系始终保持不变.
①当△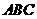 向上平移多少个单位时,△
向上平移多少个单位时,△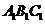 与△
与△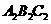 完全重合?并直接写出此时点
完全重合?并直接写出此时点 的坐标;
的坐标;
 ②将△
②将△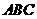 绕点
绕点 顺时针旋转
顺时针旋转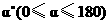 ,使△
,使△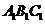 与△
与△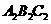 完全重合,此时
完全重合,此时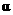 的值为多少?点
的值为多少?点 的坐标又是什么?
的坐标又是什么?
答案:解:(1)点 、
、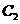 的坐标分别为
的坐标分别为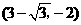 、
、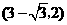 .
.
(2)能通过一次旋转将△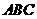 旋转到△
旋转到△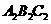 的位置,所旋转的度数为
的位置,所旋转的度数为 ;
;
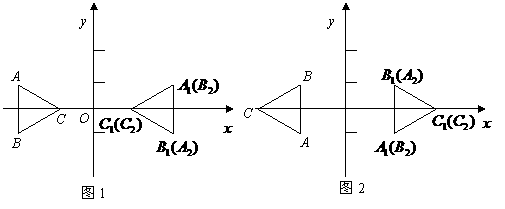
(3)①当△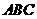 向上平移2个单位时,△
向上平移2个单位时,△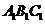 与△
与△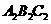 完全重合,此时点
完全重合,此时点 的坐标为
的坐标为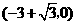 (如图1);
(如图1);
②当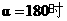 ,△
,△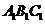 与△
与△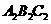 完全重合,此时点
完全重合,此时点 的坐标为
的坐标为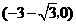 (如图2).
(如图2).
第11题. 图所示,在图甲中,Rt△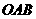 绕其直角顶点
绕其直角顶点 每次旋转
每次旋转 ,旋转三次得到右边的图形.在图乙中,四边形
,旋转三次得到右边的图形.在图乙中,四边形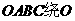 点每次旋转
点每次旋转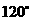 ,旋转二次得到右边的图形.
,旋转二次得到右边的图形.
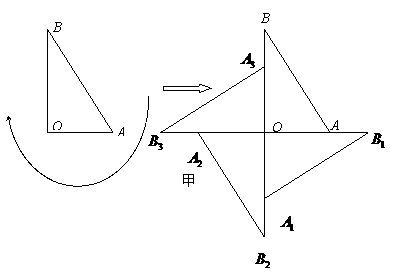
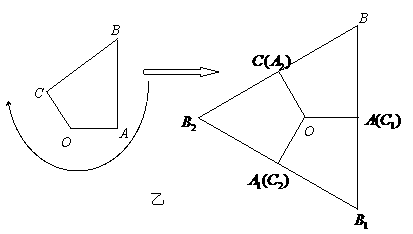
下列图形中,不能通过上述方式得到的是


(A) (B) (C) (D)
答案:D
2.若a=-5,a+b+c=-5.2,求代数式a2(-b-c)-3.2a(c+b)的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com