
题目列表(包括答案和解析)
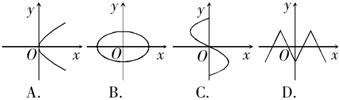
1.下面分别给出了变量x与y之间的对应关系,其中y是x函数的是( )
3.某种储蓄的月利率是0.2%,存入10000元本金,取款时应缴纳所得利息20%的利息税,则实得本息和y(元)与所存月数x之间的函数关系式为
,自变量x的取值范围是 .(不计复利)
.(不计复利)
1.当x= 时,函数y=3x+1与函数y=2x-4的函数值相等.
2 .设点P(3,m),Q(n,2)都在函数y=x+1的图象上,则m+n= .
.设点P(3,m),Q(n,2)都在函数y=x+1的图象上,则m+n= .
24. (9分)我们给出如下定义:如图① ,平面内两条直线
,平面内两条直线
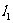 、
、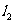 相交于点O,对于平面内的任意一点M,若p、q分别是点M到直线
相交于点O,对于平面内的任意一点M,若p、q分别是点M到直线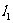 和
和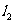 的距离(P≥0,q≥0
的距离(P≥0,q≥0 ),称有序非负实数对
),称有序非负实数对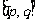 是点M的距离坐标。
是点M的距离坐标。
根据上述定义,请解答下列问题:
如图②,平面直角坐标系xoy内,直线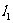 的关系式为
的关系式为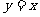 ,直线
,直线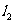 的关系式为
的关系式为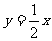 ,M是平面直角坐标系内的点。
,M是平面直角坐标系内的点。
(1)若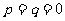 ,求距离坐标为
,求距离坐标为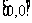 时,点M的坐标;
时,点M的坐标;
(2)若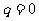 ,且
,且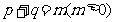 ,利用图②,在第一象限内,求距离坐标为
,利用图②,在第一象限内,求距离坐标为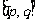 时,点M的坐标;
时,点M的坐标;
(3)若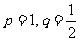 ,则坐标平面内距离坐标为
,则坐标平面内距离坐标为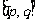 时,点M可以有几个位置?并用三角尺在图③画出符合条件的点M(简要说明画法)。
时,点M可以有几个位置?并用三角尺在图③画出符合条件的点M(简要说明画法)。
23.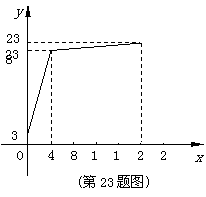 建设新农村,农村大变样.向阳村建起了天然气供应站,气站根据实际情况,每天从零点开始至凌晨4点,只打开进气阀,在以后的16小时(4∶00-20∶00),同时打开进气阀和供气阀,20∶00-24∶00只打开供气阀,已知气站每小时进气量和供气量是一定的,下图反映了某天储气量
建设新农村,农村大变样.向阳村建起了天然气供应站,气站根据实际情况,每天从零点开始至凌晨4点,只打开进气阀,在以后的16小时(4∶00-20∶00),同时打开进气阀和供气阀,20∶00-24∶00只打开供气阀,已知气站每小时进气量和供气量是一定的,下图反映了某天储气量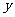 (米
(米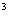 )与
)与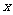 (小时)之
(小时)之 间的关系,如图所示:
间的关系,如图所示:
(1)求0∶00-20∶00之间气站每小时增加的储气量;
(2)求20∶00-24∶00时,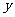 与
与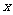 的函数关系式,并画出函数图象;
的函数关系式,并画出函数图象;
(3)照此规律运行,从这天零点起三昼夜内,经过多少小时气站储气量达到最大?并求出最大值. (8分)
22.如图,在平面直角坐标系中,直 线l是第一、三象限的角平分线.
线l是第一、三象限的角平分线.
实验与探究:
(1) 由图观察易知A(0,2)关于直线l的对称点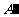 的坐标为(2,0),请在图中分别标明
的坐标为(2,0),请在图中分别标明
B(5,3) 、C(-2,5) 关于直线l的对称点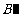 、
、 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:
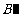 、
、  ;
;
归纳与发现:
(2) 结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点 的坐标为
(不必证明);
的坐标为
(不必证明);
运用与拓广:
(3)  已知两点D(1,-3)、E(-1,-4),试在直
已知两点D(1,-3)、E(-1,-4),试在直 线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.(8分)
线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.(8分)
21.在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:
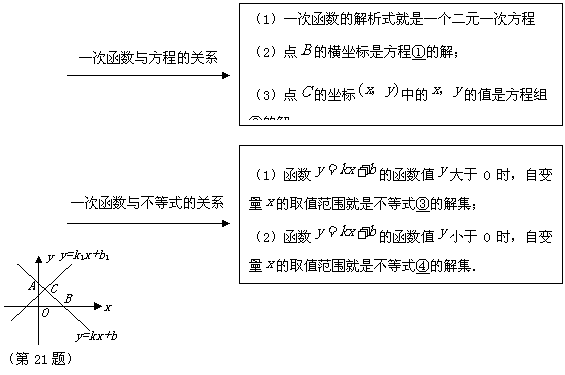
(1)请你根据以上方框中的内 容在下面数字序号后写出相应的结论:
容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ ;
(2)如果点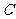 的坐标为
的坐标为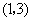 ,那么不等式
,那么不等式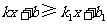 的解集是
.(7分)
的解集是
.(7分)
20.设关于x的一次函数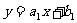 与
与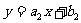 ,则称函数
,则称函数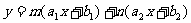 (其中
(其中 )为此两个函数的生成函数.
)为此两个函数的生成函数.
(1)当x=1时,求函数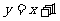 与
与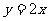 的生成函数的值;
的生成函数的值;
(2)若函数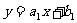 与
与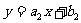 的图象的交点为
的图象的交点为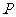 ,判断点P是否在此两个函数的生成函数的图象上,并说明理由.(7分)
,判断点P是否在此两个函数的生成函数的图象上,并说明理由.(7分)

19.已知y与x+1成正比例关系,当x=2时,y=1,求当x=-3时y 的值?(7分)
18. 已知关于x的函数同时满足下列三个条件:
①函数的图象不经过第二象限;②当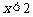 时,对应的函数值
时,对应的函数值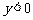 ;
;
③当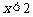 时,函数值y随x的增大而增大.
时,函数值y随x的增大而增大.
你认为符合要求的函数的解析式可以是: (写出一个即可)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com